ЛЕКЦИЯ 2. АНАЛИЗ СЛОЖНОСТИ И ЭФФЕКТИВНОСТИ АЛГОРИТМОВ И СТРУКТУР ДАННЫХ
Цели и задачи лекции:ознакомление с методами анализа сложности и эффективности алгоритмов и структур данных
Основные вопросы: экспериментальный и аналитический анализ эффективности алгоритмов.
Классическое утверждение Н.Вирта «Хорошая программа – это единство продуманного алгоритма и эффективных структур данных».
Анализ алгоритмов
Понятия “алгоритма и структур данных” являются центральными в сфере компьютерных технологий, однако, чтобы называть некоторые структуры данных и алгоритмы «качественными и эффективными», следует использовать точные приемы их анализа. В качестве естественного критерия качества естественно выделить, во-первых, время исполнения. Также важным является объем затрачиваемых ресурсов памяти и дискового пространства, скорости обращения к данным (эффективность структуры данных) . Внимание также следует уделить надежности и достоверности решений, их стабильности.
Алгоритм не должен быть привязан к конкретной реализации. В силу разнообразия используемых средств программирования различные в реализации алгоритмы могут выдавать отличающиеся по эффективности результаты.
Время выполнения алгоритма или операции над структурой данных зависит, как правило, от целого ряда факторов. Простейший способ определить затраты времени на выполнение некоторого алгоритма это провести замеры времени до запуска и после завершения работы алгоритма.
Следует, однако, помнить, что подобный способ оценки времени не является точным, прежде всего, следует понимать, что в современных операционных системах могут параллельно выполняются несколько задач и выполнение тестового примера может совместиться с иными видами активности. Далее следует понимать, что добиться устойчивой зависимости можно лишь при проведении многоразовых испытаний, иначе в причину влияния на конечный результат работы случайных факторов зависящих от специфики исходных данных, и других факторов, время выполнения алгоритма также будет случайной величиной. При проведении исследования необходимо запустить алгоритм с различным набором исходных данных, обычно сами данные генерируются случайным образом таким образом благодаря различающимся наборам данных будут отличаться также и затраты времени.
После того как будет получен набор оценок, можно построить график и провести его аппроксимацию.
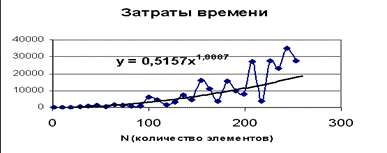
Подобный анализ всегда следует применять в случае использования не тривиальных алгоритмов, это подобно рекомендации заниматься разработкой приложения, использую для отладки не пробный набор из нескольких десятков записей или элементов, а реальные данные в полном объеме, что позволяет избежать модификации или даже полной переработки алгоритма или структур данных, если в последствии окажется их практическая не применимость. Имея набор результатов эксперимента можно провести интерполяцию и экстраполяцию и определить поведение алгоритма в реальных условиях.
В целом можно сказать, что время выполнения алгоритма или метода структуры данных возрастает по мере увеличения размера исходных данных, хотя оно зависит и от типа данных, даже при равном размере. Кроме того, время выполнения зависит от аппаратного обеспечения (процессора, тактовой частоты, размера памяти, места на диске и др.) и программного обеспечения (операционной среды, языка программирования, компилятора, интерпретатора и др.), с помощью которых осуществляется реализация, компиляция и выполнение алгоритма. Например, при всех прочих равных условиях время выполнения алгоритма для определенного количества исходных данных будет меньше при использовании более мощного компьютера или при записи алгоритма в виде программы на машинном коде по сравнению с его исполнением виртуальной машиной, проводящей интерпретацию в байт-коды.
Вывод, что проведение анализа алгоритмов эмпирическим путем не является действительно надежным. Основные недостатки можно свести к следующим трем положениям:
1) эксперименты могут проводиться лишь с использованием ограниченного набора исходных данных; результаты, полученные с использованием другого набора, не учитываются.
2) для сравнения эффективности двух алгоритмов необходимо, чтобы эксперименты по определению времени их выполнения проводились на одинаковом аппаратном и программном обеспечении;
3) для экспериментального изучения времени выполнения алгоритма необходимо провести его реализацию и выполнение.
Таким образом, мы приходим к необходимости использования для анализа алгоритмов методов общего анализа, который позволяет:
1) учитывает различные типы входных данных;
2) позволяет производить оценку относительной эффективности любых двух алгоритмов независимо от аппаратного и программного обеспечения;
3) может проводиться по описанию алгоритма без его непосредственной реализации или экспериментов.
Суть общего анализа заключается в том, что некоторому алгоритму ставится в соответствие функция f=f(n1, .., nm). В простейшем варианте это функция одной переменной n1 – количества исходных данных. Однако могут быть и другие переменные – например точность расчета или его достоверность. Так для определения того является ли некоторое число простым в случае больших чисел (длина двоичного представления более чем 200 бит) используют вероятностный метод, достоверность которого можно варьировать. Наиболее известные функции это линейные, степенные, логарифмические. Поэтому следует потратить время и вспомнить основы работы с ними.
При построении алгоритмов первая стадия идет с использованием не языка программирования, а описания на человеческом языке. Подобные описания не являются программами, но вместе с тем они более структурированы, чем обычный текст. В частности, «высокоуровневые» описания сочетают естественный язык и распространенные структуры языка программирования, что делает их доступными и вместе с тем информативными. Такие описания способствуют проведению высокоуровневого анализа структуры данных или алгоритма. Подобные описания принято называть псевдокодом. Следует также отметить, что для проведения анализа псевдокод является зачастую более полезным, чем код на конкретном языке программирования.
Иногда возникает необходимость доказать некие утверждения в отношении к определенной структуре данных или алгоритму. Например, требуется продемонстрировать правильность и быстроту исполнения алгоритма. Для строгого доказательства утверждений необходимо использовать математический язык, который, послужит доказательством или обоснованием высказываний. Существует несколько простых способов подобного доказательства.
Иногда утверждения записываются в обобщенной форме: «Множество s содержит элемент х, обладающий свойством v. Для доказательства данного утверждения достаточно привести пример х "принадлежит" s, который обладает данным свойством. В подобной обобщенной форме записываются, как правило, и маловероятные утверждения, например: «Каждый элемент х множества s обладает свойством Р». Чтобы доказать ошибочность данного утверждения, достаточно просто привести пример: х "принадлежит" s, который не обладает свойством Р. В данном случае элемент х будет выступать в качестве контр-примера.
Пример: Утверждается, что любое число вида 2^n - 1 является простым, если n — целое число, большее 1. Утверждение ошибочно.
Доказательство: чтобы доказать неправоту, обходимо найти контр-пример.
Такой контр-пример: 2^4 - 1 = 15, 15= 3 * 5.
Существует и другой способ, основанный на доказательстве от противного (использовании отрицания). Основными методами в данном случае являются контрапозиция и контрадикция. Использование методов противопоставления подобно зеркальному отражению: чтобы доказать, что «если x - истинно, то и y — истинно», будем утверждать обратное «если y — ложно, то и x — ложно». С точки зрения логики, данные утверждения идентичны, однако второе выражение, которое является котропозицией первого, более удобно.
Пример: Если a*b — нечетное число, то а - нечетное или b – нечетное.
Доказательство: для доказательства данного утверждения рассмотрим контрапозицию: «Если а — четное число и b — нечетное, то a*b – четное. Пусть, а = 2*x, для некоторого целого числа x. Тогда a*b = 2*i*b, а следовательно произведение a*b — четное.
При использовании методов доказательства от противного полезным является использование логики.
. a or b = требуется выполнение a или b, или и a и b одновременно.
. a and b = требуется одновременное выполнение a и b.
. a xor b = требуется выполнение a, но не b или же b, но не a.
При использовании метода контрадикции для доказательства того, что утверждение q — верно, вначале предполагается, что q — ложно, а затем показывается, что такое предположение приводит к противоречию (например, 2 * 2 <> 4). Придя к подобному противоречию, можно утверждать, что ситуации, при которой q - ложно, не существует, и, следовательно, q – истинно.
В большинстве случаев в утверждениях о времени выполнения программы или используемом пространстве применяется целочисленный параметр n (обозначающий «размеры» задачи). Тогда когда мы формулируем утверждение x(n), то для множества значений n подобные утверждения равносильны. Так как данное утверждение относится к “бесконечному” множеству чисел, невозможно провести исчерпывающее прямое доказательство. В подобных ситуациях используют методы индукции. Метод индукции основан на том; что для любого n > 1. Существует конечная последовательность действий, которая начинается чего-то заведомо истинного и, в конечном итоге, приводит к доказательству того, что q(n) истинно. Таким образом, доказательство с помощью индукции начинается с утверждения, что q(n) истинно при n=1,2,3 и т.д. до некоторой константы k. Далее доказывается, что следующий «шаг» индукций q(n+1), q(n+2) также является истинным для n > k.
При анализе алгоритмов, подсчете количества операций и времени их выполнения, не следует учитывать “мелкие детали”, следует пренебречь постоянными множителями и константами. На практике используют понятие функции большого О. предположим, что существуют две функции f(n) и g(n), считается, что f(n) <= O(g(n)) , т.е. функция О ограничивает сверху значения функции f, начиная с n=n0.
Например, алгоритм подсчета в массиве количества элементов равных нулю описывается О(n), где n – количество элементов.
1) 20n3+7,2n2-21,78n + 5 описывается как О(n3)
2)xn-2 + a(0) описывается как О(xn).
2) 3*log(n) + log(log(n)) описывается как О(log(n)).
3) 2100 описывается как О(1)
4) 5/n описывается как О(1/n).
Обратите внимание на то, что функция o(n) ограничивает сверху целевую функцию затрат времени, но необходимо стремиться всегда выбирать такую функцию О(n), чтобы была максимальная точность.
Наиболее известные функции О в порядке их возрастания:
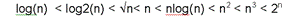
При использовании асимптотического анализа будьте внимательны, когда вы используете нотацию О, то часто пренебрегаете постоянными множителями и складываемыми константами. Однако в том случае если эта величина достаточно велика, хотя вид функции О(1) более предпочтителен, чем алгоритм, описываемый функцией О(n), но практическое применение завоюет, разумеется, именно второй алгоритм.
В зависимости от вида функции f(n) выделяют следующие классы сложности алгоритмов.
| Классы сложности алгоритмов в зависимости от функции трудоемкости | |
| Вид f(n) | Характеристика класса алгоритмов |
| Большинство инструкций большинства функций запускается один или несколько раз. Если все инструкции программы обладают таким свойством, то время выполнения программы постоянно. | |
| log N | Когда время выполнения программы является логарифмическим, программа становится медленнее с ростом N. Такое время выполнения обычно присуще программам, которые сводят большую задачу к набору меньших подзадач, уменьшая на каждом шаге размер задачи на некоторый постоянный фактор. Изменение основания не сильно сказывается на изменении значения логарифма: п |
| N | Когда время выполнения программы является линейным, это обычно значит, что каждый входной элемент подвергается небольшой обработке. |
| N log N | Время выполнения, пропорциональное N log N, возникает тогда, когда алгоритм решает задачу, разбивая ее на меньшие подзадачи, решая их независимо и затем объединяя решения. |
| N2 | Когда время выполнения алгоритма является квадратичным, он полезен для практического использования при решении относительно небольших задач. Квадратичное время выполнения обычно появляется в алгоритмах, которые обрабатывают все пары элементов данных (возможно, в цикле двойного уровня вложенности). |
| N3 | Похожий алгоритм, который обрабатывает тройки элементов данных (возможно, в цикле тройного уровня вложенности), имеет кубическое время выполнения и практически применим лишь для малых задач. |
| 2N | Лишь несколько алгоритмов с экспоненциальным временем выполнения имеет практическое применение, хотя такие алгоритмы возникают естественным образом при попытках прямого решения задачи, например полного перебора. |
На основании математических методов исследования асимптотических функций трудоемкости на бесконечности выделены пять классов алгоритмов.
1. Класс быстрых алгоритмов с постоянным временем выполнения, их функция трудоемкости O(1). Промежуточное состояние занимают алгоритмы со сложностью O(log N), которые также относят к данному классу.
2.Класс рациональных или полиномиальных алгоритмов, функция трудоемкости которых определяется полиномиально от входных параметров. Например, O(N), O(N2, O(N3).
3.Класс субэкспоненциальных алгоритмов со степенью трудоемкости O(N log N).
4.Класс экспоненциальных алгоритмов со степенью трудоемкости O(2N).
5.Класс надэкспоненциальных алгоритмов. Существуют алгоритмы с факториальной трудоемкостью, но они в основном не имеют практического применения.
Состояние памяти при выполнении алгоритма определяется значениями, требующими для размещения определенных участков. При этом в ходе решения задачи может быть задействовано дополнительное количество ячеек. Под объемом памяти, требуемым алгоритмом А для входа D, понимаем максимальное количество ячеек памяти, задействованных в ходе выполнения алгоритма. Емкостная сложность алгоритма определяется как асимптотическая оценка функции объема памяти алгоритма для худшего случая.
Таким образом, ресурсная сложность алгоритма в худшем, среднем и лучшем случаях определяется как упорядоченная пара классов функций временной и емкостной сложности, заданных асимптотическими обозначениями и соответствующих рассматриваемому случаю.
Основными алгоритмическими конструкциями в процедурном программировании являются следование, ветвление и цикл. Для получения функций трудоемкости для лучшего, среднего и худшего случаев при фиксированной размерности входа необходимо учесть различия в оценке основных алгоритмических конструкций.
- Трудоемкость конструкции "Следование" есть сума трудоемкостей блоков, следующих друг за другом: f=f1+f2+...+fn.
- Трудоемкость конструкции "Ветвление" определяется через вероятность перехода к каждой из инструкций, определяемой условием. При этом проверка условия также имеет определенную трудоемкость. Для вычисления трудоемкости худшего случая может быть выбран тот блок ветвления, который имеет большую трудоемкость, для лучшего случая – блок с меньшей трудоемкостью. fif=f1+fthen·pthen+felse·(1-pthen)
- Трудоемкость конструкции "Цикл" определяется вычислением условия прекращения цикла (обычно имеет порядок 0(1)) и произведения количества выполненных итераций цикла на наибольшее возможное число операций тела цикла. В случае использования вложенных циклов их трудоемкости перемножаются.
Таким образом, для оценки трудоемкости алгоритма может быть сформулирован общий метод получения функции трудоемкости.
- Декомпозиция алгоритма предполагает выделение в алгоритме базовых конструкций и оценку и трудоемкости. При этом рассматривается следование основных алгоритмических конструкций.
- Построчный анализ трудоемкости по базовым операциям языка подразумевает либо совокупный анализ (учет всех операций), либо пооперационный анализ (учет трудоемкости каждой операции).
- Обратная композиция функции трудоемкости на основе методики анализа базовых алгоритмических конструкций для лучшего, среднего и худшего случаев.
Особенностью оценки ресурсной эффективности рекурсивных алгоритмов является необходимость учета дополнительных затрат памяти и механизма организации рекурсии. Поэтому трудоемкость рекурсивных реализаций алгоритмов связана с количеством операций, выполняемых при одном рекурсивном вызове, а также с количеством таких вызовов. Учитываются также затраты на возвращения значений и передачу управления в точку вызова. При оценке требуемой памяти стека нужно учитывать, что в конкретный момент времени в стеке хранится не фрагмент рекурсии, а цепочка рекурсивных вызовов. Поэтому объем стека определяется максимально возможным числом одновременно полученных рекурсивных вызовов.
Дата добавления: 2018-05-10; просмотров: 2815;











