Сумма квадрата тангенса угла и единицы равна единице, деленной на квадрат косинуса этого угла.
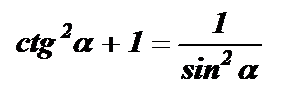 , a ¹ p k , k Î Z .
, a ¹ p k , k Î Z .
Сумма квадрата котангенса угла и единицы равна единице, деленной на квадрат синуса этого угла.
Пример:
№1. Вычислить значения остальных тригонометрических функций, если известно значение sin a = 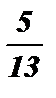 ,
, 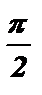 < a < p .
< a < p .
Решение: Из формулы sin 2 a + cos 2 a = 1 получаем , что cos 2a = 1 - sin 2 a .
Так как 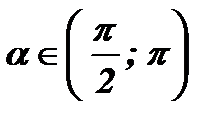 , cos a < 0 , следовательно,
, cos a < 0 , следовательно,
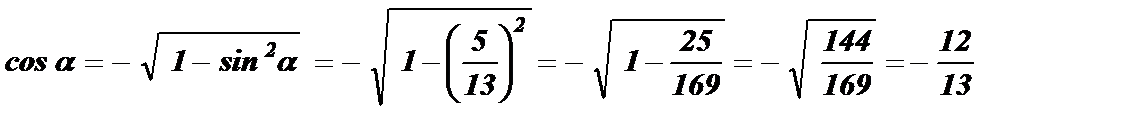 ;
;
Зная синус и косинус угла , можно найти его тангенс по формуле
 ;
; 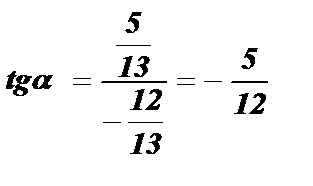 ;
;
Чтобы найти сtg a , воспользуемся формулой tg a · сtg a = 1 .
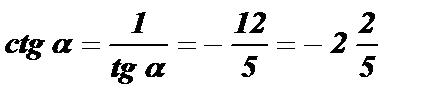 .
.
Ответ: 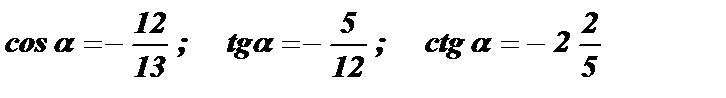 .
.
№2. Вычислить значения остальных тригонометрических функций, если известно значение tg a = 2 , 0 < a < 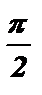 .
.
Решение: Воспользовавшись формулой 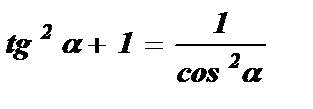 , найдем cos a :
, найдем cos a :
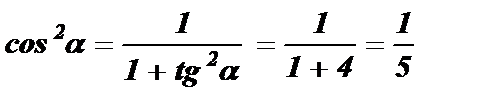 .
.
По условию a – угол 1-ой к. ч., поэтому cos a > 0.
Значит, 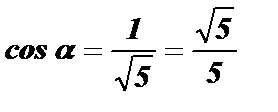 .
.
Зная косинус и тангенс угла , можно найти его синус по формуле:
tg a = 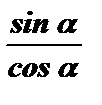 ;
;  .
.
Чтобы найти сtg a , воспользуемся формулой tg a · сtg a = 1 .
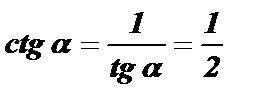 .
.
Ответ: 
№3. Упростить выражение при всех допустимых значениях a: сtg 2 a · (cos 2 a – 1).
Решение:
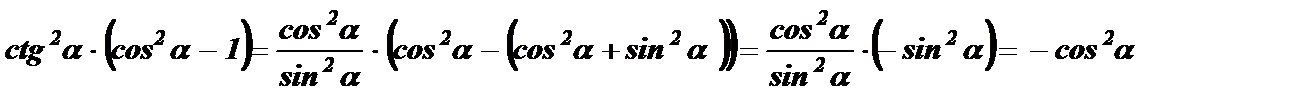
Ответ: сtg 2 a · (cos 2 a – 1) = – cos 2 a
№4. Доказать тождество: tg 2 a - sin 2 a = tg 2 a · sin 2 a
Решение: Преобразуем левую часть данного равенства:
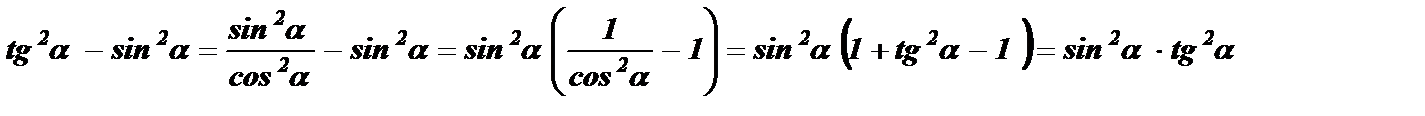
Мы получили выражение, стоящее в правой части равенства, значит, тождество доказано. Определим множество допустимых значений данного равенства. Исключаем значения переменной х , при которых не существует
tg х: х ¹ 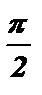 + p k, k Î Z .
+ p k, k Î Z .
Замечание: При доказательстве тригонометрических тождеств необходимо определить область допустимых значений данного равенства.
Если равенство содержит тригонометрические функции tg a и сtg a , то необходимо исключить углы a , при которых не существуют эти функции.
Если равенство содержит тригонометрические функции в знаменателе дроби, тонеобходимо исключить углы a , при которых знаменатель дроби обращается в нуль.
№5. Определить область допустимых значений тождества: 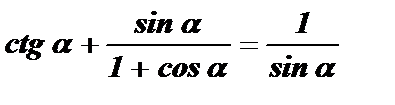
Решение:
1) Исключаем значения угла a , при которых не существует ctg a :
a ¹ p k , k Î Z ;
2) Исключаем значения угла a , при которых знаменатель дроби 1 + cos a обращается в нуль: 1 + cos a ¹ 0; cos a ¹-1; a ¹ p + 2p k , k Î Z ;
Дата добавления: 2016-05-27; просмотров: 1866;











