Дифференциальное уравнение теплопроводности и его частные случаи

В трехмерной системе координат дифференциальное уравнение теплопроводности имеет вид

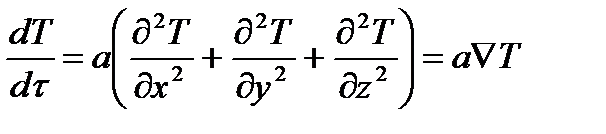
где а=λ/(сγ) – температуропроводность твердого тела,м²/с.

Выражение в круглых скобках правой части называется оператором Лапласа и обозначается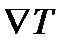

Рассмотрим частные случаи этого уравнения:

1) тепловой поток распространяется только вдоль оси х, тогда

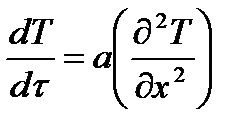
2) в выделенном элементарном объеме твердого тела температура во времени не изменяется, т.е.

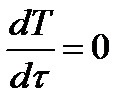
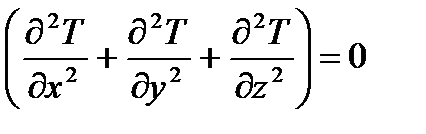
Называемое уравнением Лапласа, оно характеризует собой распределение температуры в элементарном объеме твердого тела при стационарном процессе переноса тепла (когда температура во времени во всех точках выделенного объема твердого тела остается постоянной).

3) внутренняя энергии выделенного элементарного объема твердого тела в точке с координатами х, yи zсуществует внутренний источник, выделяющий (или поглощающий) в единице объема за единицу времени количество тепла, равное А(х, y, z, τ), то дифференциальное уравнение теплопроводности имеет вид

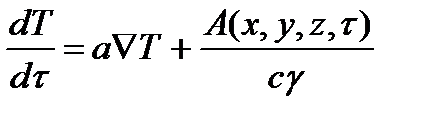
4) теплопроводность твердого тела изменяется в рассматриваемом диапазоне температур, тогда

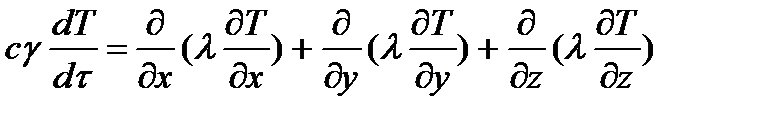
5) когда источник тепла перемещается со скоростью, компоненты которой равны V_x, V_y, V_z, тогда

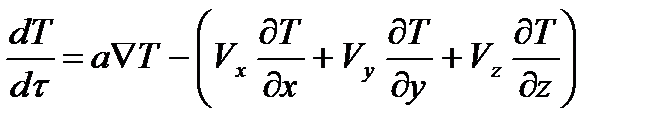
Представленные уравнения относятся к прямоугольной системе координат.

Дифференциальные уравнения теплопроводности в сферических и цилиндрических координатах имеют следующий вид:

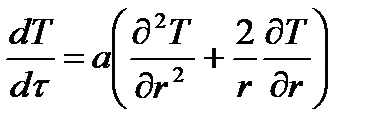и

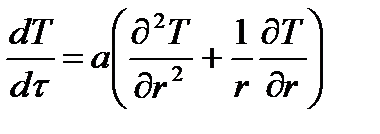
Краевые условия

Под краевыми условиями понимается совокупность начальных и граничных условий.

Начальным условием называется температурное поле в твердом теле в тот момент, с которого ведется отсчет времени температурного воздействия.

T (x,y,z,0)

Граничным условием называется условие, определяющее процесс теплообмена на границе. Понятие «граница» включает в себя внешние поверхности, подверженные тепловому воздействию, и внутренние, расположенные на некотором удалении от внешних. Граничные условия складываются из сведений об условиях теплообмена на границе и сведений об изменении параметров источника теплового воздействия.

Различают четыре рода граничных условий:

1) если известен закон изменения температуры нагреваемой поверхности во времени

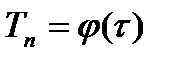
Частным случаем является постоянства температуры на поверхности, подверженной тепловому воздействию

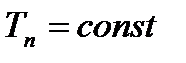
2) если известна закономерность изменения во времени удельного теплового потока, поступающего к поверхности твердого тела

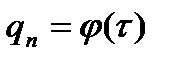или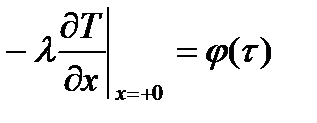

Индекс х=+0 указывает на то, что градиент температуры относится к точке тела, расположенной в непосредственной близости от поверхности.

Частным случаем имеет место при постоянстве удельного теплового потока

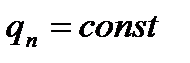
3) Если заданы температура источника теплового воздействия и интенсивность теплообмена на поверхности (теплоносителями являются жидкости и газы).

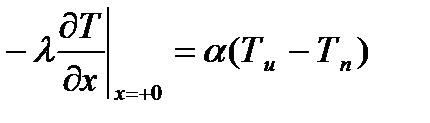
где α– коэффициент теплоотдачи, Вт/(м²К)

При установившемся режиме теплообмена коэффициент теплоотдачи можно принять постоянным.

Если нагрев твердого тела происходит за счет лучеиспускания, тогда

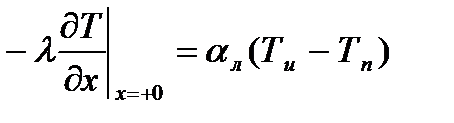
где 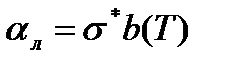, Вт/(м²К)

b(T) – коэффициент, зависящий от температуры источника и приемника лучистой энергии, К³

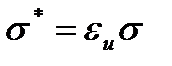- приведенный коэффициент лучеиспускания, Вт/м² ∙(К)⁴

ϭ – постоянная Стефана-Больцмана, равная 5,67∙10^-8 Вт/м²К⁴

ε – относительная излучательная способность (степень черноты) твердого тела.

4) при соприкосновении двух твердых тел с разными теплофизическими свойствами.

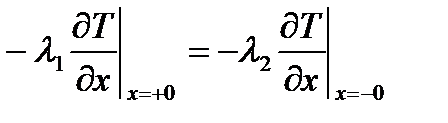
Во всех этих уравнениях в правых частях удельный тепловой поток, отводимый внутрь твердого тела от нагреваемой поверхности, в правой - математически сформулирована закономерность поступления тепла от источника к поверхности твердого тела.