Значение радиохимии

Помимо огромной роли, которую радиохимия сыграла в разра­ботке теоретических и экспериментальных основ атомной и изо­топной промышленности, отметим ее вклад в развитие естественных наук. Этот вклад определяется совокупностью фундаментальных открытий, сделанных на основе радиохимических исследований (естественная радиоактивность, превращаемость элементов, изото­пия, ядерная изомерия, искусственная радиоактивность и деление тяжелых ядер). Не меньшая роль принадлежит радиохимии в от­крытии и получении новых элементов.

Исключительную роль радиохимия сыграла в создании и раз­витии новых методов исследования. Наиболее важными из них являются радиоизотопные методы и радиохимический анализ. Зна­чение радиохимических исследований на современном этапе опре­деляется все возрастающим использованием радиоактивных нук­лидов.

Наиболее важной областью применения тяжелых нуклидов ста­новится ядерная энергетика. Одной из актуальных задач современ­ности является улучшение структуры топливно-энергетического баланса, в частности, за счет быстрого развития ядерной энергети­ки, в том числе реакторов на быстрых нейтронах, новых источни­ков энергии, включая создание термоядерной энергетики. .

Чрезвычайно важные задачи ядерная технология ставит перед радиохимическим анализом (контроль чистоты ядерных материа­лов, определение степени выгорания, изотопного состава и содер­жания делящихся материалов в ядерном топливе и др.).

На современном этапе все более широкое развитие приобрета­ет прикладная радиохимия. Радиоактивные нуклиды и радиоактив­ные излучения находят применение в самых различных областях науки и народного хозяйства.

Нельзя не отметить роли радиохимии в решении ряда экологи­ческих проблем.

2. Состояние радионуклидов в водных растворах.

Вопрос о состоянии радиоактивных изотопов, находящихся в ничтожно малых концентрациях, является одним из основных в радиохимии, так как состояние радиоактивных изотопов в зна­чительной мере определяет их поведение в различных фазах.

Под термином «состояние» в настоящее время следует пони­мать все формы нахождения радиоактивного изотопа в данной фазе; в случае растворов это прежде всего:

- простые аквоионы- M(H₂O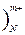

- комплексные ионы, образованные ионом металла и лигандами-{ M(H₂O)_N-iL_i}^{m-n i} ;

- моноядерные продукты гидролиза (гидроксокомплексы)- { M(OH)_i(H₂O)_N-i}^m-i ;

- полиядерные продукты гидролиза-{ M_j(OH)_i(H₂O) _jN-i}^{j m- i} ;

- истинные радиоколлоиды;

- псевдорадиоколлоиды.

Знание форм состояния радионукли­дов чрезвычайно важно, так как они определяют поведение ра­дионуклида в любых технологических операциях (сокристаллиза­ция, соосаждение, сорбция, ионный обмен, экстракция, электро­лиз и т.п.). Поэтому представляют интерес расчетные методы, позволяющие на основании справочных данных получить предва­рительную оценку концентрации (или доли) каждой из возможных форм состояния радионуклида в растворе конкретного состава.

2. Математическая модель:

2.1. Ионодисперсное состояние радионуклидов.

В отсутствии процессов радиоколлоидообразования с уче­том всех перечисленных ионных и молекулярных форм состояния радионуклидов общая аналитическая концентрация металла в водном растворе будет равна:

C_M= [M^m+] + 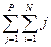[M_j(OH)_i^{j m-i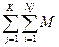}] + (L_j)_i^{m-nj ∙i}

здесь [ ] - символ концентрации данной формы; N - коорди­национное число металла в процессах гидролиза; N_j - координационное число металла по отношению к лиганду j -го типа; К -общее число лигандов различного типа, В общем случае в реаль­ном растворе может присутствовать любое число анионов ( L≡ Cl^-, SO₄^2-, CO₃^2- и др.) или молекул (L≡ NH₃), которые могут образовать комплексные ионы с металлом. Для простоты записи молекулы воды в уравнении (1) опущены.

Соответственно общая концентрация лиганда j-того типа в растворе будет равна:

С_Lj =

(Написать самостоятельно)

Примем во внимание, что образование комплексных ионов, а также взаимодействие металла и лиганда с водой происходит ступенчато в соответствии с реакциями:

M(H₂O 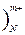+ i L_J^nj = {M (L_J)_j(H₂O)_N-i(nj) }^m-i(nj) + I (n_j)H₂O (3)

M(H₂O 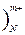+iH₂O = {M(OH)_i(H₂O)_N-i }^m-i + iH₂ O (4)

jM(H₂O 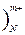+ iH₂O = {M_J (OH)_I (H₂O)_Nj--i } ^jm-I + iH₃O⁺ + jH₂O (5)

В уравнениях (3) –(5) i = 1.2,,….N.

Устойчивость образующихся форм состояния характеризуется соответствующими константами равновесия реакций (3) – (5).

Например, ступенчатое образование моноядерных гидроксокомплексов цинка (m=2, N=4) в соответствии с уравнением (4) должно быть представлено следующей системой реакций:

Zn(H₂O)₄²⁺ + H₂O = Zn (OH)(H₂O)₃⁺ + H₃O⁺ ; b₁

Zn(H₂O)₄²⁺ + 2 H₂O = Zn(OH)₂ (H₂O)₂ +2 H₃O⁺ ; b₂

Zn(H₂O)₄²⁺+ 3 H₂O = Zn(OH)₃ (H₂O)^- + 3H₃O⁺ ; b₃

Zn(H₂O)₄²⁺ + 4 H₂O = Zn(OH)₄^2- + 4 H₃O⁺ ; b₄

Где b₁ - b₄ – ступенчатые константы гидролиза

С учетом констант равновесия уравнение материального баланса для цинка может быть переписано:

С_Zn= [Zn²⁺] (1+ Σ b_i∙[H₃O⁺]^i- ). (6)

А если кроме гидроксокомплексов, имеет место образование, например, аммиачных комплексов:

Zn(H₂O)₄²⁺ + NH₃ = Zn(H₂O)₃ (NH₃ )²⁺ ; k₁

Zn(H₂O)₄²⁺ + 2NH₃ = Zn(H₂O)₂ (NH₃ )₂²⁺ ; k₂

Zn(H₂O)₄²⁺ + 3NH₃ = Zn(H₂O) (NH₃ )₃²⁺ ; k₃

Zn(H₂O)₄²⁺ + 4NH₃ = Zn (NH₃ )₄²⁺ ; k₄

То уравнение материального баланса будет иметь вид:

С_Zn= [Zn²⁺] (1+ Σ b_i∙[H₃O⁺]ⁱ + Σk_i[NH₃]ⁱ). (7)

Уравнение материального баланса для лиганда можно записать:

C_L= [Hn_jL_j] Σ Kд_i ∙ [H₃O⁺]^-I +[M^m+]Σ i∙k_i∙[L^nj]ⁱ

Таким образом, во многих случаях еще до постановки эксперимента можно получить количественную картину форм состояния.

Очень наглядно зависимость химического состояния радионуклида от концентрации лиганда и величины рН, может быть выражена с помощью степени образования (или доли) i –той формы металла или лиганда - α_i.

Зная состав раствора (С_M, С_L. рН) и располагая сведениями о значениях констант образования соответствующих комплексов, можно рассчитать распределение радионуклида по ионодисперсным формам состояния, используя соответствующие уравнения.

Рассмотрим для наглядности соответствующие примеры.

1. Состояние цинка в растворе в отсутствие лигандов-комплексообразователей.

В этом случае доли всех возможных форм состояния цинка в растворе будут вычисляться по уравнениям:

α_Zn(2+)=[Zn²⁺]/ С_Zn= 1/(1+ Σ b_i∙[H₃O⁺]^i-)

α_Zn(OH)+ = α_Zn(2+) ∙ b_1∙ [H₃O⁺]^-

α_Zn(OH)2 = α_Zn(2+) ∙ b₂ ∙[H₃O⁺]^2-

и т.д. и т.п.

Соответствующая диаграмма распределения моноядерных гидроксокомплексов цинка представлена на рисунке.

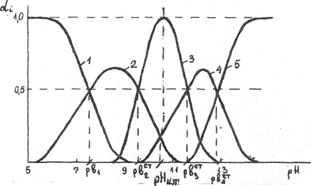
Диаграмма распределения гидроксокомплексов цинка в зависимости от рН раствора

1-Zn²⁺; 2-Zn(OH)⁺;3-Zn(OH)₂;

4- Zn(OH)₃^-; 5- Zn(OH)₄^2-

Точно также может быть получена диаграмма распределения различных форм слабых кислот и оснований. Для примера на рис. 2 представлена диаграмма для угольной кислоты.

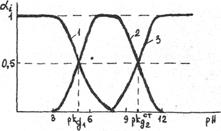
Диаграмма распределения различных форм угольной кислоты в зависимости от рН раствора

2. 2. Коллоидное состояние радионуклидов.

Изучение состояния радионуклидов в водных растворах первоначально сводилось к ре­шению вопроса о природе коллоидного состояния растворов поло­ния, висмута и свинца в очень разбавленных водных растворах и привело к представлению о том, что их образование не связано с радиоактивными процессами.

В настоящее время можно считать доказанным, что для образования истинных коллоидов радио­элементов не требуется особых условий, связанных с радиоактив­ным распадом, а достаточно соблюдения основного условия обра­зования коллоидов — достижения произведения растворимости.

2. Коллоидное состояние радионуклидов.

2. I. Истинные радиоколлоиды.

Истинные радиоколлоиды представляют из себя труднораст­воримые соединения, образованные радионуклидом с тем или иным анионом-осадителем. Основой рассмотрения термодинамичес­кого равновесия в гетерогенной системе: “оcадок труднораство­римого соединения МnLт - водный раствор”

M_nL_m = M_nL_m = nMⁿ⁺ + mL^n-

является произведение активностей (ПА), которое согласно Ненсту определяется выражением

ПА= a_(Mm+)ⁿ ∙a _(Ln-)^m

где a- термодинамическая активность,

При данной температуре ПА - величина постоян­ная.

В условиях постоянства ионной силы раствора коэффициен­ты активности можно считать постоян­ными и для характеристики гетерогенного равновесия пользо­ваться выражением:

ПР= [M^m+]ⁿ∙[L^n-]^m

Учтем, что [M^m+] = α (M ^m+)∙C_M и

[L^n-] = α(L^n-)∙ C_L

а суммарные равновесные концентрации в водном растворе всех форм катиона и аниона осадка будут равны со­ответственно

C_M = n∙ C_p и C_L= m∙C_p , где С_p - растворимость данного осадка в его насыщенном растворе, моль/л.

Тогда после некоторых преобразований получим урав­нение растворимости.

ПР= [M^m+]ⁿ∙[L^n-]^m =(n∙ α _M m+ ∙ C_p)ⁿ ∙( α_Ln-∙ C_L)^m = nⁿ ∙^\( α _M m+∙)ⁿ ∙C_pⁿ ∙ (α_Ln-)^m ∙C_L^m.

Далее:

С_p= (ПР)^1/n / n∙ α _M m+ ∙ (α_Ln-)^m/n. (C_L)^m/n

pC_p= pПР- pn-pα _M m+ - m/n ∙pα_Ln- -m/npC_L

Это уравнение может быть использовано для оценки термодинамической вероят-ности образования труднорастворимого соединения в растворе любого состава. При этом если рассчитанная по данному уравнению растворимость меньше общей аналитической концентрации металла (С_о), то раствор является пересыщенным и образование истинных коллоидов радионуклидов термодинамически вероятно. При С_р> С_о раствор является ненасыщенным и образования истинных коллоидов ожидать не следует. Долю истинных коллоидов можно рассчитать по уравнению:

Α_и.к. =(С_о-С_р) /С_о

Обычно считают, что основной причиной образования радионуклидами истинных коллоидов является гидролиз, приво­дящий к формированию самостоя-тельной фазы труднорастворимого гидроксида металла. Уравнение для растворимости гидроксида металла со стехиометрической растворимости для гид­роксида металла со стехиометрии-ческой формулой М (ОН)_m будет иметь

pC_p = pПР_г+ mpH-mpK_w- pα_M^m+

Данное уравнение легко получить из уравнения для произведения растворимости учитывая, что

С_L =[OH^-], α_OH =1

Из уравнения растворимости гидроксида видно, что при наличии твердой фазы гидроксида неизвестная при данном значении рН концентрация аквоиона может быть вычислена непосредственно из величины ПР_г:

P[M^m+]= pC_P + pα_M^m+=pПР_Г+mpH -mpK_W

Следовательно, в этом случае можно предложить другой алгоритм расчета форм состояния радионуклидов в водном раст­воре, отличающийся от изложенного ранее.

В данном случае представляется возможность сначала непосредственно рассчитать концентрацию i-той формы, а потом ее долю. Дей­ствительно, если решить уравнения для расчета долей соответствующих частиц относительно кон­центрации i-той формы и сделать соответствующие подстановки, то из правой части полученных уравнений видно, что они содержат только справочные величины.

Так, например, для гидроксокомплекса металла M(OH)_i^m-i уравнение будет иметь вид:

P[M(OH)_i^m-i ] = pПР_Г -mpK_W +pb_i +

(m-i)pH

Покажем это на конкретном примере:

M^m+ + iH₂O = M(OH)_i^m-I + iH⁺

b_i = [M(OH)_i^m-i] ∙ [H⁺]^I / [M^m+];

lg[M(OH)_i^m-i] = lg[M^m+] +lg b_i -ilg[H⁺] =

lgПР - mlgK_W +mlg[H⁺] + lg b_i -ilg[H⁺]=

lgПР - mlgK_W+ lg b_i + (m-i) lg[H⁺].

Аналогичным образом можно рассчитать концентрации, а также доли других форм.

Далее для заданных концентраций рН и лиганда для всех концентраций рН (с шагом ΔрН) рассчитываем суммарную концентрацию растворенных форм металла ( растворимость) по уравнению

pC_p= pПР- pn-pα_Mm+ - m/n ∙pα_Ln- -m/n∙pC_L

и получаем зависимость растворимости гидроксида от рН. Долю радионуклида, находящегося в форме истинных коллоидов рассчитываем по уравнению:

pα_ик =p(C₀ – C_P) - pC_P

Для наглядности на рис. 3 и 4 показан общий вид кривых осаждения и растворимости амфотерного и неамфотерного гидроксидов для случая C_L=0.

На рисунках приняты следующие обозначения:

рН₀- величина рН начала образования коллоидов;

рН_к- величина рН конца растворения осадка гидроксида или рН начала осаждения гидроксида из щелочного раствора;

С₀- начальная или общая концентрация металла в растворе;

С_min- минимальная растворимость осадка гидроксида, или минимальная концентрация металла, ниже которой образование осадка гидроксида металла не следует ожидать.

Если концентрация лиганда не равна нулю, то на кривых растворимости может быть несколько экстремумов.

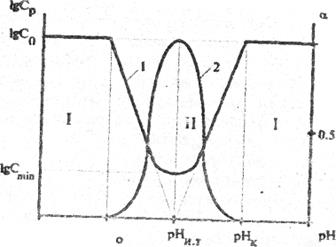
Рис. 3 Принципиальный график кривых растворимости (1) и