Двоичные функции одного аргумента
Известно, что от одного двоичного аргумента x может быть образовано четыре разных двоичных функций yj = Fj(x). Значения этих функций приведены в табл. 1.
Таблица 1
n = 1
| X | y0 | y1 | y2 | y3 | ||||
| 21 | ||||||||
| 21 | 20 | |||||||
N = 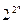 = 4 = 4
| ||||||||
Функция y0 сохраняет нулевое значение, а функция y3 - единичное значение при любом значении аргумента. Двоичная функция, сохраняющая нулевое или единичное значение при любом наборе значений аргументов, называется соответственно константой нуля (y0=0) или константой единицы (y3=1).
Функция y1 принимает значение, равное значению ее аргумента. Такая функция y1=x называется тавтологией. Ее реализует логический элемент повторитель, условное графическое обозначение которого приведено на Рис. 3, а.
Функция y2 принимает значение, противоположное значению ее аргумента. Такая функция называется инверсией. Операция отыскания значения инверсии по заданному значению ее аргумента называется операцией отрицания или операцией НЕ. Для обозначения операции отрицания используется запись следующего вида:
y = 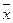 .
.
Произносится: y равно НЕ x. Функция инверсия реализуется логическим элементом - инвертором, УГО которого приведено на Рис. 3, б.
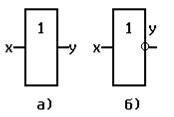
Рис. 3 Элементарные автоматы без памяти (двоичные функции одного аргумента)
Дата добавления: 2017-11-21; просмотров: 1251;











