Пространства со скалярным произведением
Введём еще одну дополнительную характеристику в пространстве сигналов в отображения упорядоченной пары векторов на поле скаляров из F.
Эту операцию называют скалярным (внутренним) произведением векторов и записывают в виде: 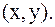
1. Если 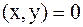 , то вектора х и у ортогональны.
, то вектора х и у ортогональны.
2. Если 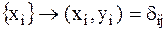 –символ Кронекера:
–символ Кронекера: 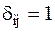 при
при 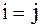 и
и
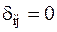 при
при 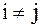 , система векторов – ортонормированная.
, система векторов – ортонормированная.
Система ортонормированных векторов линейно независимая.
В линейном пространстве со скалярным произведением норму и метрику целесообразно определять через скалярное произведение.
В ТЭС наибольший интерес представляют следующие линейные нормированные пространства:
1. 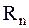 – n-мерное вещественное евклидово пространство, в котором каждый вектор определяется совокупностью n его координат.
– n-мерное вещественное евклидово пространство, в котором каждый вектор определяется совокупностью n его координат.
Скалярное произведение векторов в этом пространстве:
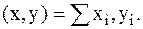
| (2.1) |
Оно порождает норму и расстояние:
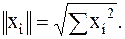
| (2.2) |
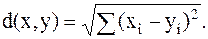
| (2.3) |
Пример:определения нормы и метрики Евклида в декартовой системе координат: заданы два вектора (сигнала) 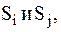 положение которых полностью определено их координатами
положение которых полностью определено их координатами 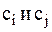 (рисунок 2.1).
(рисунок 2.1).
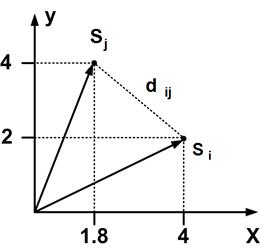
|
| Рисунок 2.1 – Определения нормы и метрики Евклида в декартовой системе координат |
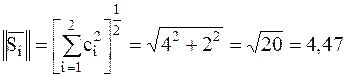
|
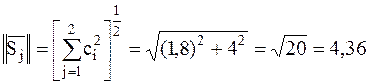
|
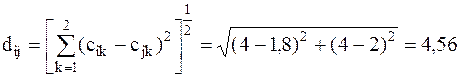
|
Расстояние между векторами 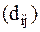 определяет различимость сигналов. Чем больше расстояние (метрика), тем лучше различимы сигналы. Метрика Евклида применяется при декодировании свёрточных кодов с помощью алгоритма Витерби с мягким решением. Выигрыш от применения мягкого решения в отношении сигнал/шум по сравнению с жёстким решением составляет 2,5 дБ (при квантовании продетектированного сигнала на 8 уровней).
определяет различимость сигналов. Чем больше расстояние (метрика), тем лучше различимы сигналы. Метрика Евклида применяется при декодировании свёрточных кодов с помощью алгоритма Витерби с мягким решением. Выигрыш от применения мягкого решения в отношении сигнал/шум по сравнению с жёстким решением составляет 2,5 дБ (при квантовании продетектированного сигнала на 8 уровней).
2. 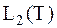 – бесконечномерное пространство Гильберта, которое образуют непрерывные комплексные или вещественные функции, заданные на интервале (0,Т):
– бесконечномерное пространство Гильберта, которое образуют непрерывные комплексные или вещественные функции, заданные на интервале (0,Т):
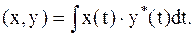
| (2.4) |
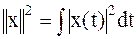 – квадрат нормы – это энергия сигнала, если под
– квадрат нормы – это энергия сигнала, если под 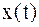 иметь ввиду напряжение (ток) на сопротивлении 1 Ом. Энергию разностного сигнала можно представить следующим выражением:
иметь ввиду напряжение (ток) на сопротивлении 1 Ом. Энергию разностного сигнала можно представить следующим выражением:
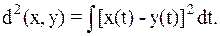
| (2.5) |
В пространстве Гильберта определяется квадрат расстояния между любой парой сигналов (векторов). Величина 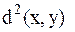 полностью характеризует различие между сигналами.
полностью характеризует различие между сигналами.
3. 2n – n-мерное пространство Хэмминга, которое образуют двоичные n-последовательности, широко используемые в системах связи.
Норма, метрика в этом пространстве:
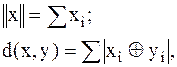
| (2.6) | |||
| где | 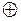
| – | суммирование по модулю «2». | |
Норма вектора в пространстве Хэмминга определяется общим количеством содержащихся в нём единиц, а расстояние между векторами – количеством позиций (разрядов) кодовых комбинаций, в которых они различаются.
Примеры:
1. Задана кодовая комбинация (вектор в пространстве Хэмминга): 1011010. Определить норму.
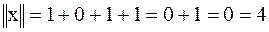 – норма данного вектора. Норма вектора в пространстве Хэмминга совпадает с количеством единиц в кодовой комбинации, т.е. с весом кодовой комбинации.
– норма данного вектора. Норма вектора в пространстве Хэмминга совпадает с количеством единиц в кодовой комбинации, т.е. с весом кодовой комбинации.
2. Заданы две кодовые комбинации: 1001011 и 0110010. Определить расстояние (метрику) в пространстве Хэмминга между кодовыми комбинациями.
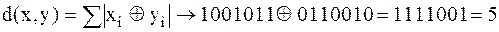
|
Метрика (расстояние) между кодовыми комбинациями равна 5. Метрика Хэмминга находит широкое применение при декодировании свёрточных кодов по алгоритму Витерби с жёстким решением. Чем больше метрика Хэмминга, тем сильнее различима кодовые комбинации.
Выводы
1. Векторное представление применимо как для детерминированных функций, так и для случайных. В последнем случае скалярное произведение, норма и расстояние – случайные величины.
Дата добавления: 2017-11-21; просмотров: 780;










