Кодирование и модуляция.

Преобразование дискретных и непрерывных сообщений в сигналы

Кодирование и модуляция.

Преобразование дискретного сообщения в сигнал обычно осуществляется с помощью двух операций – кодирование и модуляция.

Кодирование представляет собой преобразование сообщения в последовательность кодовых символов, а модуляция – преобразование этих символов в сигналы, пригодные для передачи по каналу. С помощью кодирования и модуляции источник согласуется с каналом.

Для передачи букв русского алфавита необходимо передать числа от 0 до 31. Для передачи любого числа, записанного в десятичной форме, требуется передача десяти цифр – от 0 до 9. На практике для этого нужны десять сигналов, которые соответствуют различным цифрам. Систему передачи дискретных сообщений можно упростить, если воспользоваться при кодировании двоичной системой счисления. Известно, что в качестве основания счисления можно принять любое целое число 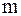. Поэтому любое число N можно представить в следующем виде:

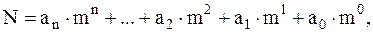
	(1.1)
где		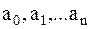–	коэффициенты, принимающие значения от 0 до (m-1).

Задаваясь величиной 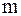можно построить любую систему счисления.

При 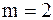получается двоичная система, в которой числа записываются с помощью двух цифр «1» и «0». Например, число 12 в двоичной системе записывается 1100, что соответствует выражению 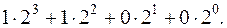Сложение в двоичной системе осуществляется путём поразрядного сложения без переноса в старший разряд («сложение по модулю два»). Правила этого сложения следующие: 0+0=0; 0+1=1; 1+0=1; 1+1=0.

Если преобразовать последовательность элементов сообщения в последовательность двоичных чисел, то для передачи последних по каналу связи достаточно передать всего лишь два различимых сигнала. Например, символы «0» и «1» могут передаваться колебаниями с различными частотами или импульсами тока разной полярности. Благодаря своей простоте двоичная система счисления широко применяется при кодировании дискретных сообщений.

Процесс кодирования заключается в преобразовании элементов сообщения в соответствующие имчисла(кодовые символы). В результате этой операции каждому элементу сообщения присваивается определённая совокупность кодовых символов, которая называется кодовой комбинацией. Совокупность кодовых комбинаций, отображающих дискретные сообщения, образует код. Множество возможных кодовых символов называется кодовым алфавитом, а их количество m – основанием кода. Число разрядов n, образующих кодовую комбинацию, называется разрядностью кода или длиной кодовой комбинации. В зависимости от системы счисления, используемой при кодировании, различают двоичные и m-ичныекоды.

Коды, у которых все комбинации имеют одинаковую длину, называют равномерными. Для равномерного кода число возможных комбинаций равно 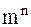. Примером такого кода является код Бодо, который содержит пять двоичных элементов (m=2, n=5). Число возможных комбинаций равно 2⁵=32, что достаточно для кодирования всех букв русского алфавита. Однако этого недостаточно для передачи сообщений, содержащих буквы, цифры, различные условные знаки. Поэтому в настоящее время широко используется «Международный код №2» (МТК-2). В этом коде применён регистровый принцип, согласно которому одна и та же пятиэлементная кодовая комбинация может использоваться до трёх раз в зависимости от положения регистра: русский, латинский, цифровой. Общее число различных знаков при этом равно 84, что вполне достаточно для кодирования телеграммы.

Для передачи данных рекомендован семиэлементный код МТК-5. Коды МТК-2 и МТК-5 являются первичными (простыми). Данные коды не позволяют обнаруживать и исправлять ошибки, которые могут возникнуть в канале связи под влиянием помех. Основным признаком, по которому можно отнести код к простому является отсутствие проверочных символов в кодовых комбинациях. Основными параметрами кодов являются: основание кода m, длина кодовой комбинации n, расстояние между кодовыми комбинациямиd, вес кодовой комбинации. Расстояние характеризует различие между двумя кодовыми комбинациями и определяется в пространстве Хэмминга. Число ненулевых элементов в кодовой комбинации определяет её вес. В настоящее время равномерные коды находят широкое применение, так упрощают построение автоматических буквопечатающих устройств и не требуют передачи разделительных символов между кодовыми комбинациями.

Неравномерные коды характеризуются тем, что у них кодовые комбинации отличаются друг от друга не только взаимным расположением символов, но их количеством. Это приводит к тому, что различные комбинации имеют различную длительность. Неравномерные коды требуют либо специальных разделительных знаков, указывающих конец одной и начало другой кодовой комбинации, либо должны строиться так, чтобы никакая кодовая комбинация не являлась началом другой. Коды, удовлетворяющие этому условию, называют неприводимыми илипрефиксными. Типичным примером неравномерных кодов является код Морзе, в котором символы 0 и 1 используются в двух сочетаниях – как одиночные (1 и 0) или как тройные (111 и 000). Сигнал, соответствующий одной единице, называется точкой, трём единицам – тире. Символ 0 используется как знак, отделяющий точку от тире, точку от точки и тире от тире. Совокупность 000 используется как разделительный знак между кодовыми комбинациями.

По корректирующей способности коды делятся на примитивные (первичные) и корректирующие. Коды, у которых все возможные кодовые комбинации используются для передачи информации, называют простыми или кодами без избыточности (примитивными).В простых равномерных кодах превращение одного символа комбинации в другой (0→1 или 1→0), приводит появлению новой разрешённой кодовой комбинации, т. е. к появлению ошибки. Корректирующие коды строятся так, что для передачи сообщения используются не все кодовые комбинации, а лишь некоторая их часть (разрешённые кодовые комбинации). С помощью этой операции создаётся возможность обнаружения и исправления ошибки при неправильном воспроизведении некоторого числа символов. Корректирующие свойства кодов достигаются введением в кодовые комбинации избыточности.

Декодирование состоит в восстановлении сообщения по принятым символам. Устройства, осуществляющие кодирование и декодирование называются соответственно кодером и декодером. Как правило, это логические устройства.

В системах передачи дискретных сообщений принято различать две группы самостоятельных устройств: кодеки и модемы.

Кодеком называют устройства, преобразующие сообщение в код (кодер) и код в сообщение (декодер), а модемом – устройство, преобразующее код в сигнал (модулятор) и сигнал в код (демодулятор).

Модуляция

Одним из этапов преобразования сообщения в сигнал для его передачи в канал связи является модуляция.

Модуляция – изменение какого-либо параметра переносчика сигнала в соответствии с функцией отображающей сообщение.

Несущим сигналом может быть: постоянный ток – проводная телеграфия; переменный ток низкой или высокой частоты – телефония, тональная телеграфия, фототелеграф, телемеханика; высокочастотные импульсы - радиорелейная связь.

Модулируемые параметры называются информативными, и в качестве них могут использоваться: амплитуда; фаза; частота и др.

Используются следующие типы модуляции: гармоническая; импульсная; дискретная и их разновидности.

Демодуляция – отделение полезного (модулирующего) сигнала от несущей. Модуляция и демодуляция осуществляется с помощью устройств, называемых модулятором и демодулятором.

Модем– устройство, преобразующее код в сигнал (модулятор) и сигнал в код (демодулятор), используемое для передачи данных по каналам связи.

Манипуляция – модуляция, при которой модулируемый параметр может принимать фиксированное число – m дискретных значений.