Интегрирование по частям и замена переменной в определенном интеграле
Поскольку вычисление определенного интеграла с помощью формулы Ньютона-Лейбница свелось к отысканию первообразной (неопределенного интеграла), то естественно перенести на случай определенного интеграла и все приемы нахождения неопределенного интеграла.
Например, непосредственное интегрирование:
а) 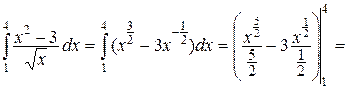
= 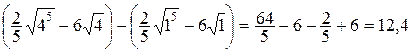 .
.
б) 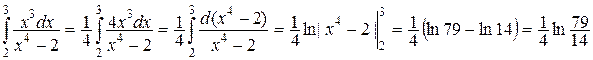 .
.
Метод интегрирования по частям в определенном интеграле основан на формуле

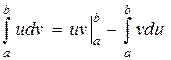 .
.
Выводится эта формула так же, как и соответствующая формула в неопределенном интеграле.
Рассмотрим пример ее применения:
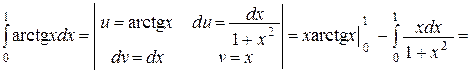
= 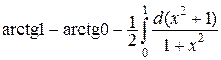
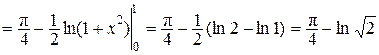 .
.
Метод замены переменной в определенном интеграле имеет некоторые отличия от соответствующего метода в неопределенном.
Пусть требуется вычислить 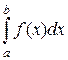 , где f(x) непрерывная на [a, b] функция. Сделаем подстановку х = j(t), полагая при этом, что:
, где f(x) непрерывная на [a, b] функция. Сделаем подстановку х = j(t), полагая при этом, что:
1) j(t) и j¢(t) непрерывны на некотором отрезке [a; b];
2) j(a) = а, j(b) = b;
3) f(j(t)) определена и непрерывна на [a; b].
Тогда
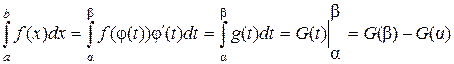 .
.
Таким образом, правило замены переменных в определенном интеграле таково:
1. Выбрать замену х = j(t) (или t = y(x)).
2. Преобразовать подынтегральное выражение f(x)dx с помощью этой замены к виду g(t)dt .
3. Найти новые пределы интегрирования a и b из условия j(a) = а, j(b) = b (или, соответственно, a = y(а), b = y(b) ).
4. Вычислить 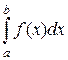 =
= 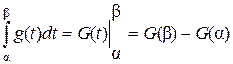 .
.
Отличие он замены переменной в неопределенном интеграле состоит в том, что получив искомую первообразную, не нужно возвращаться к старой переменной. Заметим при этом, что в процессе замены переменной интегрирования обязательно меняются пределы интегрирования.
Рассмотрим пример.
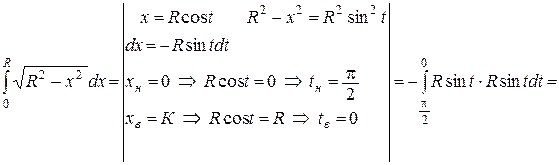
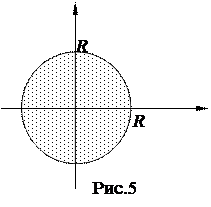
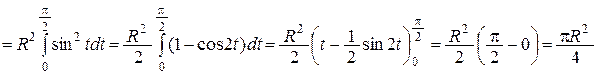
Заметим, что с геометрической точки зрения, этот интеграл численно равен площади четверти круга с центром в начале координат и радиусом R , т.к. линия 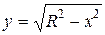 есть четверть соответствующей окружности, расположенная в первой координатной четверти (рис.5). Тогда площадь полного круга равна pR2 – т.е. мы доказали с помощью определенного интеграла известную формулу площади круга.
есть четверть соответствующей окружности, расположенная в первой координатной четверти (рис.5). Тогда площадь полного круга равна pR2 – т.е. мы доказали с помощью определенного интеграла известную формулу площади круга.
Замечание. Функции-замены обязательно должны быть непрерывны на соответствующем промежутке. Например, для вычисления интеграла 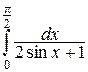 подстановку
подстановку 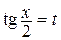 применить можно, так как на отрезке
применить можно, так как на отрезке 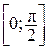 эта функция непрерывна, а для вычисления интеграла
эта функция непрерывна, а для вычисления интеграла 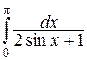 – такую подстановку применить нельзя, т.к. в точке х = p функция
– такую подстановку применить нельзя, т.к. в точке х = p функция 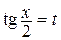 имеет бесконечный разрыв.
имеет бесконечный разрыв.
С помощью замены переменных можно доказать следующие важные свойства определенного интеграла:
1) Если f(x) четная функция, то 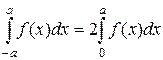 .
.
Например,
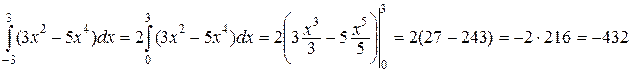
2) Если f(x) нечетная функция, то 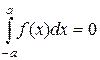 . Например,
. Например, 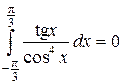 , т.к. функция
, т.к. функция 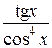 – нечетная.
– нечетная.
3) Если f(x) периодическая функция с периодом Т, то 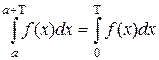 "а.
"а.
Докажем эти свойства. 1) Пусть f(x) = f(–x). Тогда
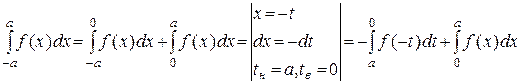 =
=
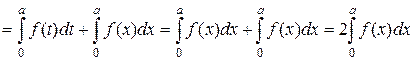 .
.
2) Пусть f(–x) = –f(x). Тогда
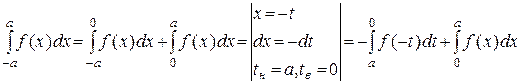 =
=
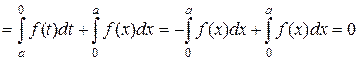
3) Пусть f(x+Т) = f(x). Можно записать
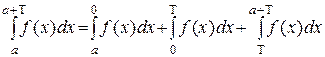 .
.
Рассмотрим 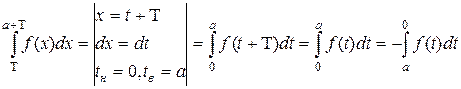 . Тогда предыдущее равенство будет иметь вид
. Тогда предыдущее равенство будет иметь вид
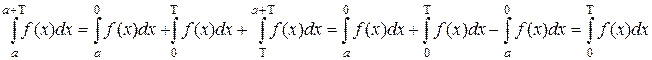
Дата добавления: 2017-11-21; просмотров: 1591;











