Третий тип задач - прямая и поверхность не имеют вырожденных видов

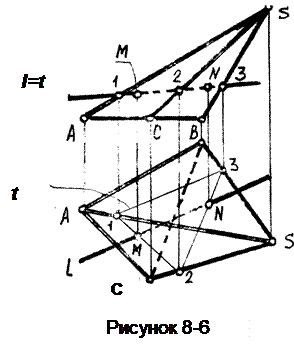Пример 6. Построить точки пересечения М и N прямой с поверхностью пирамиды (рисунок 8-6).

Чтобы найти точки пересечения необходимо на поверхности многогранника построить конкурирующую с l ломаную линию и определить их взаимное положение.

Построим, например, фронтально-конкурирующую ломаную линию t . Пересечение l и t на виде сверху определяет точки пересечения М и N прямой l с поверхностью пирамиды. Находим эти точки на виде спереди.

Видимость точек М и N определяем по видимости граней которым они принадлежат. Точка М принадлежит видимой грани ASС, значит она и участок прямой влево от т. М - видимы. Точка N принадлежит невидимой грани SСВ, значит участок вправо от т. М до контура пирамиды будет невидим. На виде спереди эти грани видны, поэтому и прямая l, кроме участка МN, будет видна.

Пример 7. Построить точки пересечения М и N прямой l с 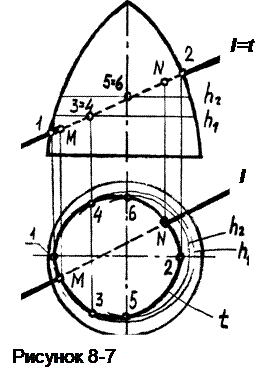поверхностью вращения (рисунок 8-7).

Построим на поверхности вращения линию t, фронтально-конкурирующую с прямой l. Ее изображение на виде сверху построено по точкам (метод принадлежности точки и поверхности).

Видимость точек М и N определена по видимости участков поверхности вращения. На виде сверху видна вся поверхность, значит т.т. М и N видны, видна и прямая l (кроме участка MN).

На виде спереди т. М видна, т. N не видна, т.к. лежит на поверхности за главным меридианом.

При построении конкурирующей линии необходимо стремиться к тому, чтобы эта линия была графически простой, что упрощает решение задачи.

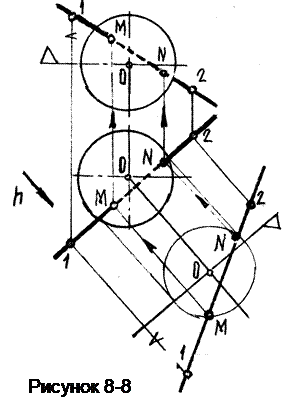
Иногда с целью упрощения решения задачи прибегают к построению дополнительного вида (рисунок 8-8). Конкурирующая линия на поверхности сферы – окружность, которая на любом из видов изображается эллипсом.

Чтобы не строить по точкам эллипс, построим дополнительный вид по направлению горизонтали h, на нем конкурирующая линия изобразится окружностью. Здесь точки пересечения находятся легко.