ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ УГЛА

Используя свойства ортогональной проекции прямого угла, можно решать задачи на определение натуральной величины угла между:

· двумя скрещивающимися прямыми;

· двумя пересекающимися прямыми;

· угла наклона прямой к плоскости;

· угла между двумя пересекающимися плоскостями.

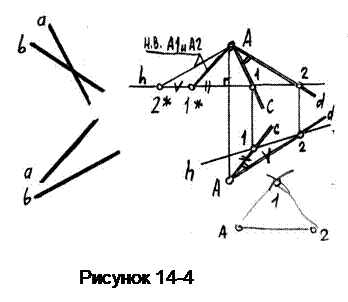
Пример 12. Определить натуру угла между скрещивающимися прямыми aиb(рисунок 14-4).

Через произвольную точку А проведем прямые си d, параллельные прямым а и b. В полученной плоскости проведем горизонталь и построим натуральную величину Δ А-1-2 (способом засечек, предварительно определив натуру каждой его стороны).

Угол при вершине А будет искомым.

Пример 13. Определить угол наклона прямой n к плоскости 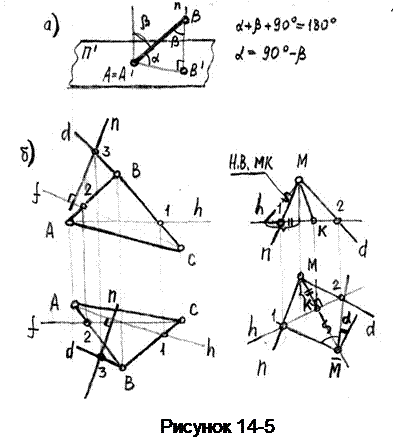Б (ΔАВС), (рисунок 14-5).

Угол наклона прямой к плоскости можно рассматривать как дополнительный угол до .90°между данной прямой и нормалью к плоскости (рисунок 18-а, угол β).

Для решения задачи из произвольной точки 3 прямой dстроим нормаль n к плоскости Б. Затем определяем угол между двумя пересекающимися прямыми d и n, для чего через произвольную точку М проводим прямые, параллельные d и n.

Определяем натуру угла между ними; угол дополняющий его до 90° будет искомым.

Пример 14. Определить угол между двумя пересекающимися плоскостями Б(α//b) и Д (с´d) (рисунок 14-6).

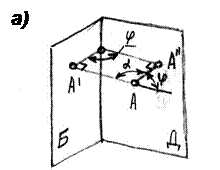Натуральная величина угла между двумя плоскостями измеряется линейным углом, дополняющим до 180° угол между перпендикулярами, опущенными из произвольной точки А на данные плоскости (рисунок 14-6а).

α+φ+90˚=360˚; α+φ=180˚; φ=180˚-α.

Плоские углы φ и αравны линейным углам двух смежных двугранных углов, образованных плоскостями Б и Д.

Алгоритм решения задачи:

1) Вначале находим точку А лежащую на линии пересечения плоскостей (14-6б).

2) Затем восстанавливаем из этой точки перпендикуляры к обеим плоскостям – Б и Д (рисунок 14-6б).

3) Определяем угол между нормалями к плоскостям из Δ1-2-М, построенного по натуральным величинам его сторон засечками (рисунок 14-6в).

Искомый угол φ=180˚-α(рисунок 14-6г).

г)