Приведенной длиной физического маятника называется длина математического маятника период, которого совпадает с периодом физического маятника.

Это определение позволяет легко определить выражение для приведенной длины.

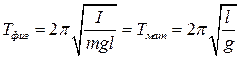
Сравнивая эти выражения получим

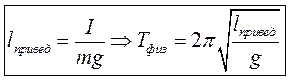
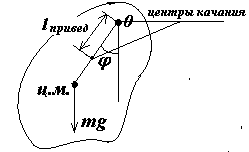
Если на линии проведенной от точки подвеса через центр масс физического маятника отложить (начиная от точки подвеса) приведенную длину физического маятника, то в конце этого отрезка будет точка, которая обладает замечательным свойством. Если физический маятник подвесить за эту точку, то его период колебаний будет тот же, что и в случае подвешивания маятника в прежней точке подвеса. Эти точки называются центрами качания физического маятника.

Рассмотрим еще одну простейшую колебательную систему совершающую гармонические колебания

Пружинный маятник

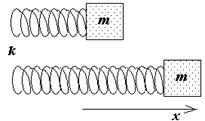Представим, что к концу пружины с коэффициентом жесткости k прикреплен груз массой m.

Если мы переместим груз вдоль оси х растянув пружину то на груз будет действовать возвращающая в положение равновесия сила F_возвр= - kx . Если груз отпустить, то эта сила вызовет ускорение d²x /dt². Согласно второму закону Ньютона мы получим:

md²x /dt² = - kx из этого уравнения получаем уравнение колебания груза на пружине в окончательном виде: d²x /dt ²+ (k/m)x = 0

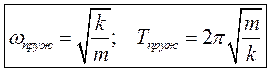Это уравнение колебаний имеет такой же вид как и уравнения колебаний в уже рассматриваемых случаях, а это значит, что решением этого уравнения будут такие же гармонические функции. Частота и период колебаний будут соответственно равны

Причем сила тяжести ни коем образом не влияет на колебания пружинного маятника. Так как в этом случае она является постоянно действующим фактором , действующим все время в одну сторону и не имеющая ничего общего с возвращающей силой.

Таким образом как мы видим колебательный процесс в механической колебательной системе характеризуется прежде всего наличие в системе возвращающей силы действующей на систему, а сами колебания характеризуются: амплитудой колебания их периодом, частотой и фазой колебаний.