Квантовая теория строения атома водорода.

В атоме водорода вокруг ядра (протона), несущего заряд e, движется один электрон. Ядро можно считать неподвижным, поскольку его масса в 1840 раз больше массы электрона; орбиты электрона в первом приближении можно считать круговыми.

Центростремительной силой, удерживающей электрон на орбите радиусом r, является кулоновская сила притяжения между электроном и ядром:

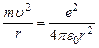, (14)

m - масса электрона, 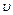- его скорость, .

Решая (14) совместно с (12), получим выражение для радиуса стационарной орбиты атома водорода:

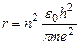, (15)

где n = 1, 2, 3, … . Для n = 1, r₁ ≈ 0.53 .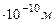

Полная энергия W электрона в атоме слагается из кинетической энергии W_к поступательного движения электрона по орбите и потенциальной энергии W_п притяжения электрона к ядру.

Учитывая (14), получим

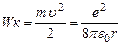(16)

Потенциальная энергия должна быть отрицательна и равна

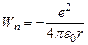(17)

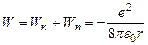(18)

Т.е. полная энергия электрона оказывается отрицательной и равной по абсолютной величине его кинетической энергии. Подставляя в (18) выражение для r из (15), получим

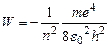(19)

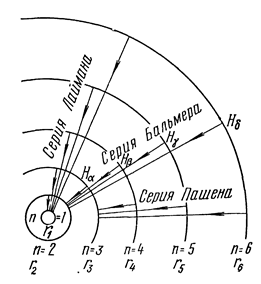
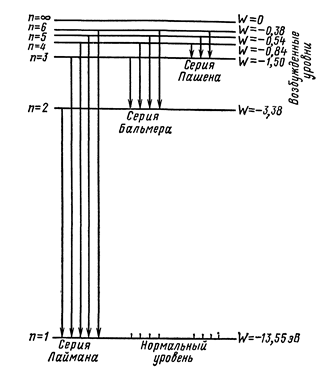
По этой формуле можно рассчитать энергию электрона для любой стационарной орбиты. Величина полной энергии электрона, находящегося на стационарной орбите, называется уровнем энергии атома.

Согласно (19), энергия атома возрастает с увеличением квантового числа n, или с увеличением радиуса электронной орбиты. Так как W отрицательна, уменьшение ее абсолютной величины соответствует возрастанию энергии.

Энергетический уровень W = - 13,55 эВ называется нормальным уровнем, все остальные уровни называются возбужденными.

Выведем общую формулу для частоты 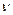излучения атома. Для этого (19) подставим в (13):

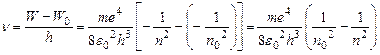, (20),

где n и W соответствуют начальным состояниям атома (до излучения), а n₀ и W₀ – после излучения,

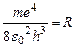, (21)

– постоянная Ридберга,

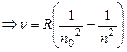(22)

Эмпирические формулы (9), (10) и (11) являются частными случаями (22).