Функции распределения скоростей ветра

Для изучения ветрового режима в местах отсутствия метеорологических станций или недостаточности метеорологических станций в непосредственной близости от места предполагаемой установки ВЭУ прибегают к построению аналитической (теоретической) кривой повторяемости скорости ветра. Математические аппроксимации эмпирических повторяемостей скоростей ветра аналитическими или табулированными функциями t^м(V) определяются статистическим моделированием, основанным на обработке имеющихся реальных эмпирических повторяемостей скоростей ветра t(V), полученных на сети метеорологических станций. Оценить точность математических аппроксимаций можно сравнением с реальными эмпирическими повторяемостями скоростями ветра. В качестве критерия точности применения аналитического или табулированного распределения можно принять среднеквадратичное отклонение данных эмпирической кривой распределения от модельных. При этом количественной мерой погрешности принимают среднеквадратичное отклонение s в процентах (%), рассчитанное по разности повторяемостей модельных t^м(V) и фактических значений t(V) с учетом переменной величины градаций скоростей ветра. Допустимое максимальное среднеквадратичное отклонение s теоретической кривой повторяемости скорости ветра t^м(V) от эмпирической t(V) принято для условий России 6 %. Окончательно из нескольких рассматриваемых моделей предпочтение следует отдать той t^м(V), среднеквадратичное отклонение s которой от эмпирической t(V) будет наименьшим.

В качестве наиболее распространенных для аппроксимации повторяемостей ветра по скоростям в отечественной ветроэнергетике в середине прошлого века являлись табулированные распределения Поморцева, Гуллена, Колодина, Гринцевича. Наиболее общепринятыми для аппроксимации t(V)в зарубежной практике в настоящее время являются двухпараметрическая функция Вейбулла, которая также является основой аппроксимации в европейской методике и дает хорошие результаты аппроксимации для многих регионов России, что подтвердили проведенные расчеты на кафедре НВИЭ МЭИ (ТУ). Полученные результаты показали, что наиболее точные способы восстановления функции распределения ветра в условиях России дают двухпараметрическое распределение Вейбулла и табулированное распределение Гринцевича.

Математическое выражение двухпараметрического распределения Вейбулла имеет вид:

t(V) = × × ,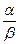

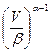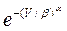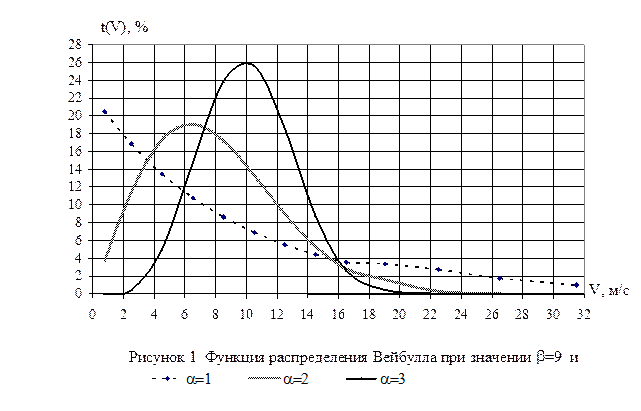
где a и b - параметры функции распределения Вейбулла, параметр a определяет форму рассматриваемой кривой распределения, а параметр b - масштабный параметр скорости. В качестве примера ниже представлен график зависимости t(V) для трех значений параметра a = 1, 2, 3 при постоянном значении параметра b=9.

При a=1 функция распределение Вейбулла носит название экспоненциального, при a=2 распределение имеет специальное название – однопараметрическое распределение Рэлея, принятое базовым для аппроксимации в американской методике.

Разработаны различные методы определения параметров a и b функции распределения Вейбулла: ниже подробно рассматриваются два метода определения параметра a функции распределения Вейбулла :

1. По формуле Л.Б. Гарцмана:

a= С_V^-1,069,

где С_V, б/р – коэффициент вариации скоростей ветра, который обычно известен для опорной метеостанции либо может быть рассчитан по формуле.

2. Графический метод с использованием логарифмической клетчатки вероятностей ГГО им. А.И. Воейкова.

Используется свойство: кривая обеспеченности скоростей ветра F_i(V_i), построенная в логарифмической системе координат на клетчатке вероятностей ГГО им. А.И. Воейкова, представляет собой зависимость близкую к линейной с коэффициентом наклона a.

Параметр a. определяется численным методом и равен котангенсу угла наклона F_i(V_i), т.е.

a = сtg(b) = АВ(мм)/ВС (мм).

Точность определения a существенно зависит от точности построения линейной зависимости F_i(V_i), особенно в диапазоне скоростей от 5 м/с до
20 м/с, так как именно в этой зоне скоростей функция Вейбулла хорошо аппроксимирует реальную повторяемость скоростей ветра.

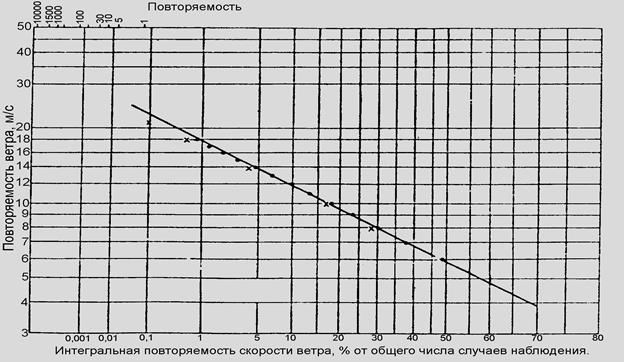
Рисунок - Графическое определение параметра a по логарифмической клетчатке вероятностей ГГО им. А.И. Воейкова

Второй параметр двухпараметрического распределения функции Вейбулла - b (о.е.) может быть определен по формуле:

b = ,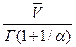

где `V, м/с – средняя скорость за рассматриваемый период времени (обычно среднемноголетняя или среднегодовая) на высоте флюгера (10 м); Г(1+1/a), о.е. – значение гаммы функции.

Восстановление распределения по табулированному распределению Гринцевича происходит по значению среднегодовой (среднемноголетней) скорости V_о, лежащей между значениями средних скоростей ветра V_оj и
V_оj+1 (см. исходные данные таблица 1). Тогда частоты распределения ветра t(V_i^гр), соответствующие i –ым градациям ветра, находятся линейной интерполяцией:

t^Гр (V_гр)= t_i ^j + [ ( t_i ^j+1- t_i ^j) / (V_оj+1- V_оj) ] * (V_о- V_j),

где t_i ^j, t_i ^j+1, % - частоты распределения ветра, соответствующие i –ым градациям ветра для средних скоростей ветра V_оj и V_оj+1 .

Cреднеквадратичное отклонение аппроксимирующей зависимости от фактической повторяемости скоростей ветра s определяется по формуле:

s= ,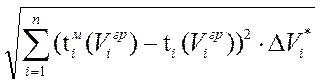

где t^м_i(V_i^гр) - теоретическая повторяемость, рассчитанная по формуле Вейбулла или табулированному распределению Гринцевича; t_i(V_i^гр) – заданная исходная повторяемость; DV_i ^* в о.е. рассчитывается по формуле

DV_i ^* =DV_i /V ^max,

где DV_i – диапазон i-й градации

ЛЕКЦИЯ № 11

В околоземном слое на изменение скорости влияет множество факторов: шероховатость местности, погодные условия, высота и т.д.

Скорости ветра как правило приводят к сравниваемым условиям :

· условия открытой ровной местности с учетом К_р;

· высота флюгера 10 м от поверхности Земли.