Разрыв и объединение эквипотенциальных узлов.
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: 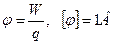 - энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. В отсутствии сторонних сил (источников) в ветви, разность потенциалов совпадает с напряжением.
- энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. В отсутствии сторонних сил (источников) в ветви, разность потенциалов совпадает с напряжением.
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. Отсутствие разности потенциалов на концах проводника, имеющего сопротивление, приводит к отсутствию тока в нем.
Рассмотрим теперь две схемы, изображенные на рисунках снизу.
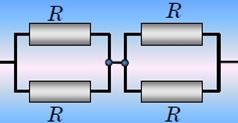
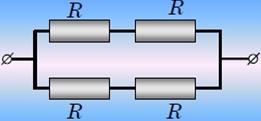
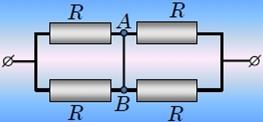 Элементарные расчеты, приводят к результату: сопротивления обеих цепей равны R. Является ли это совпадение случайным? Схема а, превращается в схему б, если соединить проводником точки А и В. Однако из симметрии схемы следует, что электрический ток по этому проводнику АВ не пойдет. Действительно, в какую сторону ему идти? − оба направления равноправны. Еще одним доказательством отсутствия тока в этом проводнике является равенство потенциалов точек А и В.
Элементарные расчеты, приводят к результату: сопротивления обеих цепей равны R. Является ли это совпадение случайным? Схема а, превращается в схему б, если соединить проводником точки А и В. Однако из симметрии схемы следует, что электрический ток по этому проводнику АВ не пойдет. Действительно, в какую сторону ему идти? − оба направления равноправны. Еще одним доказательством отсутствия тока в этом проводнике является равенство потенциалов точек А и В.
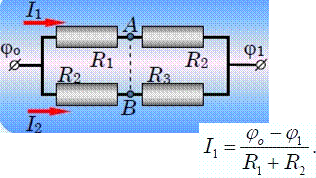
Рассмотрим общую схему такого соединения с произвольными значениями сопротивлений резисторов и вычислим потенциалы точек А и В. Сила тока через последовательно соединенные резисторы R1 и R2 определяется законом Ома
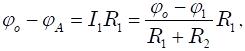 Разность потенциалов на резисторе R1 равна
Разность потенциалов на резисторе R1 равна
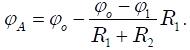 поэтому потенциал точки А равен
поэтому потенциал точки А равен
Аналогичные рассуждения для нижней ветви цепи позволяют записать потенциал точки В
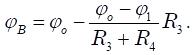
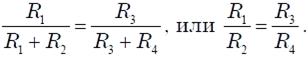 Итак, условие отсутствия тока между точками А и В при их соединении точек, следующее из равенства потенциалов φA = φB, имеет вид
Итак, условие отсутствия тока между точками А и В при их соединении точек, следующее из равенства потенциалов φA = φB, имеет вид
Рассмотрим способы нахождения точек одинакового потенциала более подробно. Пусть нам дана электрическая цепь, состоящая из сопротивлений R1, R2, …, R8.
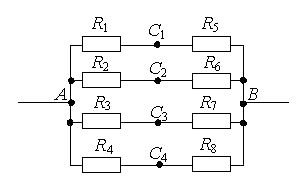 Проведем через точки подключения цепи прямую АВ.
Проведем через точки подключения цепи прямую АВ.
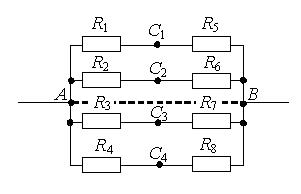 1 способ. Если схема содержит проводники с одинаковым сопротивлением, расположенные симметрично относительно определенной оси или плоскости, то концы этих проводников имеют одинаковый потенциал. При этом точки будут симметричными относительно прямой АВ, если равны сопротивления участков цепи между данными точками и любыми точками этой прямой.
1 способ. Если схема содержит проводники с одинаковым сопротивлением, расположенные симметрично относительно определенной оси или плоскости, то концы этих проводников имеют одинаковый потенциал. При этом точки будут симметричными относительно прямой АВ, если равны сопротивления участков цепи между данными точками и любыми точками этой прямой.
Используя этой признак, можно сделать вывод, что точки C1 и C2 будут симметричны относительно прямой АВ, если R1 = R2 (сопротивления между точкой А и C1 и между точкой А и C2 равны) и R5 = R6 (сопротивления между точкой В и C1 и между точкой В и C2 равны). Аналогично, точки C3 и C4 будут симметричны относительно прямой АВ, если R3 = R4 и R7 = R8.
2 способ. Точки имеют одинаковый потенциал, если равны отношения сопротивлений между данными точками и точками подключения.
Например, точки C1 и C2 имеют одинаковый потенциал, если R1/R2=R5/R6 . Аналогично, точки C3 и C4 имеют одинаковый потенциал, если R3/R4=R7/R8 .
Метод объединения эквипотенциальных узлов: точки с одинаковыми потенциалами можно соединять в узлы.
 В некоторых случаях точки цепи, имеющие одинаковый потенциал, определяются просто, исходя из симметрии схемы. В таких ситуациях расчет электрического сопротивления значительно упрощается: во-первых, если такими точками включены элементы цепи, то их можно отбросить, так как электрический ток через них не течет; во-вторых, точки равного потенциала можно соединить проводником − это не приведет к изменению сопротивления, так как распределение токов в цепи не изменится.
В некоторых случаях точки цепи, имеющие одинаковый потенциал, определяются просто, исходя из симметрии схемы. В таких ситуациях расчет электрического сопротивления значительно упрощается: во-первых, если такими точками включены элементы цепи, то их можно отбросить, так как электрический ток через них не течет; во-вторых, точки равного потенциала можно соединить проводником − это не приведет к изменению сопротивления, так как распределение токов в цепи не изменится.
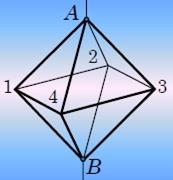
Рассчитаем, например, сопротивление каркасного октаэдра, изготовленного из проволоки, сопротивление каждого ребра которого равно R. При подключении источника тока к противоположным вершинам А и В, точки 1, 2, 3, 4 равноправны, поэтому имеют одинаковый потенциал. Следовательно, ток не течет по ребрам октаэдра, соединяющим эти вершины, поэтому, их можно отбросить, не нарушая распределения токов по остальным ребрам. Тогда сопротивление каркаса становится эквивалентным сопротивлению четырех параллельно соединенных ветвей, состоящих из двух ребер, общее сопротивление равно R/2.
Найдем сопротивление проволочного куба, сопротивление каждого ребра которого равно R, при подключении источника тока к противоположным вершинам А и В. 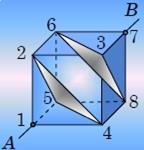 Вершины куба 2, 4, 5 находятся на расстоянии одного ребра от точки «входа» А, поэтому их потенциалы равны, следовательно, их можно соединить между собой, не нарушая при этом распределения токов по ребрам куба. Аналогично, можно соединить между собой вершины 3, 6, 8. Таким образом, точка А оказывается соединенной с «объединенной точкой 2, 4, 5» тремя параллельно соединенными ребрами, от «точки 2, 4, 5» до «точки 3, 6, 8» включено параллельно шесть ребер, и далее до выхода, точки В, еще три параллельно соединенных ребра. Таким образом, получаем эквивалентную схему рассматриваемого каркаса, общее сопротивление которой рассчитывается элементарно:
Вершины куба 2, 4, 5 находятся на расстоянии одного ребра от точки «входа» А, поэтому их потенциалы равны, следовательно, их можно соединить между собой, не нарушая при этом распределения токов по ребрам куба. Аналогично, можно соединить между собой вершины 3, 6, 8. Таким образом, точка А оказывается соединенной с «объединенной точкой 2, 4, 5» тремя параллельно соединенными ребрами, от «точки 2, 4, 5» до «точки 3, 6, 8» включено параллельно шесть ребер, и далее до выхода, точки В, еще три параллельно соединенных ребра. Таким образом, получаем эквивалентную схему рассматриваемого каркаса, общее сопротивление которой рассчитывается элементарно:

Если возможно объединение двух равнопотенциальных узлов, то возможен и обратный переход:
-
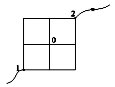 узел схемы можно разделить на два или несколько узлов, если получившиеся при этом узлы имеют одинаковые потенциалы – метод разделения узлов.
узел схемы можно разделить на два или несколько узлов, если получившиеся при этом узлы имеют одинаковые потенциалы – метод разделения узлов.
Пример:
Металлическая сетка с сопротивлением звена R. Рассчитать сопротивление между точками 1 и 2.
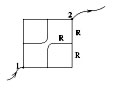 В центральной точке можно звенья отделить, тогда схема будет иметь вид:
В центральной точке можно звенья отделить, тогда схема будет иметь вид: 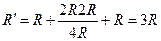 - сопротивление одной половины симметричной по 1-2 точкам. Параллельно ей такая же ветвь, поэтому
- сопротивление одной половины симметричной по 1-2 точкам. Параллельно ей такая же ветвь, поэтому 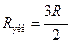
Дата добавления: 2017-11-21; просмотров: 4334;











