Магнитодвижущая сила секции

Секция является простейшим элементом трехфазной обмотки. Поэтому для определения результирующей МДС трехфазной обмотки рассмотрим сначала МДС секции. Пусть на статоре уложено по одной секции на каждом полюсном делении. Шаг секции 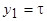. По секциям протекает ток 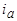, равный току параллельной ветви фазы:

.

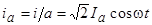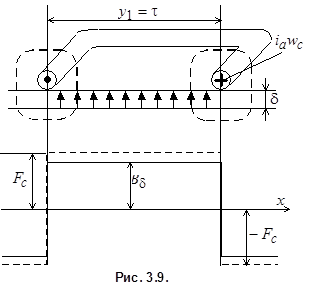
Вид возникающего при этом магнитного поля на одном полюсном делении показан на рис. 3.9. Любая силовая линия магнитного поля сцеплена с полным током секции 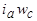, поэтому поле, созданное секцией, будет постоянным на протяжении всего полюсного деления,

.

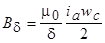Будем считать магнитную индукцию положительной, если силовые линии идут вверх (южный полюс), и отрицательной, если силовые линии идут вниз (северный полюс). В соответствии с этим условием при принятом направлении тока поле внутри секции будет положительным, образующим южный полюс, а за пределами секции - отрицательным, образующим северный полюс.

МДС секции, приходящуюся на один полюс, обозначим через 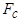. При равномерном воздушном зазоре МДС каждого полюса равны, поэтому

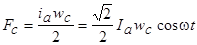. (3.3)

МДС секции изменяется скачком при пересечении активной стороны секции, увеличиваясь, если ток направлен к нам, и уменьшаясь, если ток направлен от нас. Величина скачка МДС равна полному току секции 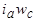(рис. 3.9, пунктирная линия).

Таким образом, МДС секции представляет собой неподвижную в пространстве прямоугольную волну, пульсирующую, согласно (3.3), во времени с частотой питающей сети.

Для дальнейшего анализа поля удобно пространственную кривую МДС разложить в ряд Фурье. Выполним разложение кривой МДС (рис. 3.10) в пределах полюсного деления для момента времени 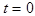, когда МДС секции принимает максимальное значение

.

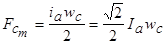Начало отсчета совместим с магнитной осью секции. Исходная функция является четной и симметричной относительно оси абсцисс, поэтому в разложении будут содержаться только нечетные гармоники с косинусными членами:

,

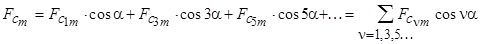где 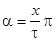- пространственный угол; n - порядок гармоники.

Амплитуды гармонических составляющих определяются по формуле

.

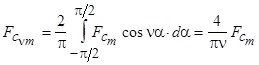Первая гармоника называется основной, а остальные - высшими пространственными гармониками. Амплитуда высшей гармоники обратно пропорциональна ее порядку. Среди высших гармоник наиболее значительными являются 3-я, 5-я, 7-я гармоники.

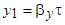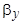Эффективным способом подавления высших гармоник является укорочение шага секции. На рис. 3.11 представлена МДС секции с укороченным шагом , где - относительный шаг секции.

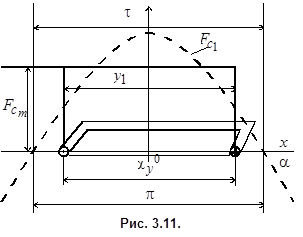
В угловом измерении шаг определяется величиной

.

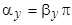Раскладывая кривую (рис. 3.11) в ряд Фурье, получим

,

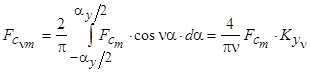где 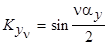- коэффициент укорочения шага обмотки.

Если выбрать шаг секции равным 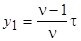, то гармоническая составляющая n порядка становится равной нулю:

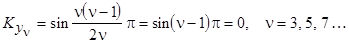
Укорочение шага используют для подавления, главным образом, 5-й и 7-й гармоник, выбирая шаг 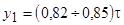. При этом первая гармоника уменьшается незначительно 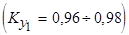. Третья гармоника и кратные трем гармоники МДС не оказывают влияния на результирующее поле трехфазной обмотки (см. п. 3.3), поэтому никаких специальных мер для их подавления не применяют.