Взаимосвязь индексов
Система взаимосвязанных индексов позволяет выявить и оценить роль отдельных факторов в изменении данного явления, т.е. показать, как изменился результативный показатель под влиянием каждого отдельного фактора.
1. 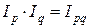 индекс товарооборота в фактических ценах,
индекс товарооборота в фактических ценах,
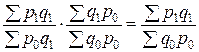
2. 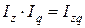 – индекс затрат на продукцию,
– индекс затрат на продукцию,
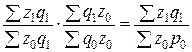 .
.
Система взаимосвязанных индексов используется на практике для определения роли отдельных факторов в общей динамике сложного явления и для определения по двум известным показателям третьего неизвестного.
3. Средневзвешенные индексы
Преобразование агрегатного индекса в средневзвешенный производится путем подстановки либо в числитель либо в знаменатель агрегатного индекса его значения через соответствующий индивидуальный индекс. Если такая замена сделана в числителе соотношения, индекс окажется преобразованным в средний арифметический, если в знаменателе, то в средний гармонический.
Практически замена делается обычно там, где в агрегатном индексе отсутствует условная экономическая величина.
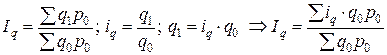 – индекс физического объема средний арифметический,
– индекс физического объема средний арифметический,
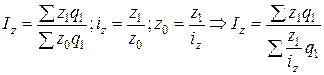 – индекс себестоимости средний гармонический.
– индекс себестоимости средний гармонический.
4. Индексный метод анализа динамики среднего уровня
Индексный метод анализа динамики предполагает наличие системы взаимосвязанных индексов, в которой:
индекс переменного состава = индекс фиксированного состава 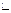 индекс структурных сдвигов,
индекс структурных сдвигов,
где индекс переменного состава отражает изменение среднего уровня показателя за счет двух факторов:
1) изменение качественного показателя;
2) изменение удельных весов, т.е. структуры совокупности.
Индекс фиксированного состава выявляет влияние качественного показателя, 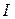 структурных сдвигов характеризует динамику среднего показателя за счет изменений в структуре совокупности.
структурных сдвигов характеризует динамику среднего показателя за счет изменений в структуре совокупности.
Из формулы средней
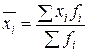 следует,
следует,
что на среднюю величину оказывает влияние как значение осредняемого признака 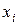 , так и численность отдельных вариантов изучаемой совокупности
, так и численность отдельных вариантов изучаемой совокупности 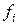 .
.
Так, на среднюю цену овощей, продаваемых на рынках, влияют как различия индивидуальных цен, так и изменения объема реализации. Поэтому при анализе изменения цен важно определить, в какой мере это вызвано изменениями индексируемых величин и в какой – структурными сдвигами количества реализованной продукции.
Таким образом, получаем, что общий индекс средней величины (индекс переменного состава) строится по формуле:
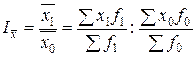 .
.
Индекс, характеризующий изменения средней величины вследствие изменений величин осредняемого признака у отдельных единиц совокупности – индекс постоянного (фиксированного) состава:
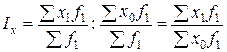 .
.
Индекс, характеризующий изменения средней величины вследствие изменений в структуре совокупности – индекс структурных сдвигов:
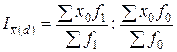 .
.
Получим систему взаимосвязанных индексов средней величины:
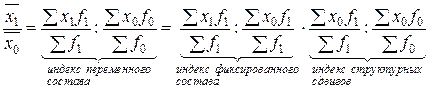 , т.е.
, т.е.
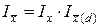 .
.
Можно вычислять эти же индексы, используя удельные веса,
т.е. 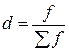 ,
, 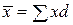 . Тогда получим следующие формулы:
. Тогда получим следующие формулы:
Индекс переменного состава: 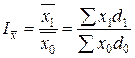 .
.
Индекс постоянного состава: 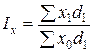 .
.
Индекс структурных сдвигов: 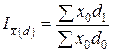 .
.
Пример:
| Товар | Ед. изм. | I период | II период | Инд. индексы | |||
цена за ед. измерения, руб. 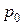
| кол-во 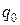
| цена за ед. измерения, руб. 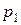
| кол-во 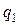
| цен 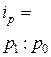
| физ. объема 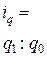
| ||
| А | т | 1,25 | 1,27 | ||||
| Б | м | 1,0 | 1,25 | ||||
| В | шт. | 0,67 | 1,5 |
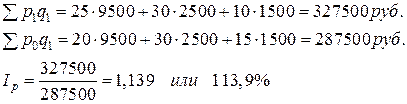
При сравнении числителя и знаменателя формулы в разности определяется показатель абсолютного прироста товарооборота за счет фактора изменения цен в текущем периоде по равнению с базисным периодом:
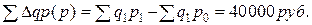
Полученная величина прироста говорит о том, что повышение цен на данный ассортимент товаров в среднем на 13,9% обусловило увеличение объема товарооборота в текущем периоде на 40 тыс.руб. Величина этого показателя (с противоположным знаком, т. е. – 40 тыс. руб.) характеризует перерасход денежных средств населением при покупке товаров данного ассортимента по ценам, повышенным на 13,9%.
Вычислим то же по формуле Ласпейреса:
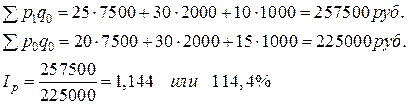
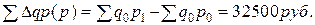
Полученная сумма прироста товарооборота показывает, что повышение цен в текущем периоде в среднем на 14,4% обусловливает увеличение объема товарооборота на 32,5 тыс. руб.
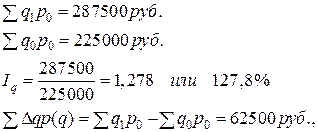
т. е. в результате изменения физического объема реализации товаров в текущем периоде получен прирост объема товарооборота в сопоставимых ценах на 62,5 тыс. руб.
Агрегатный индекс физического объема товарооборота может определяться посредством использования в качестве соизмерителя индексируемых величин 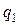 и
и 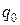 цен текущего периода
цен текущего периода 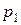 .
.
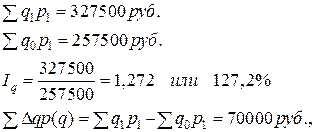
т. е. применение формулы (7) показывает, что по данному ассортименту реализованных в текущем периоде товаров прирост физического объема товарооборота составил 27,2%.
Общий индекс товарооборота в текущих ценах составляет: 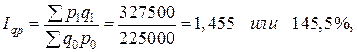 т.е. в текущем периоде товарооборот в фактических ценах возрос по данному ассортименту товаров по сравнению с базисным периодом в среднем на 45,5%.
т.е. в текущем периоде товарооборот в фактических ценах возрос по данному ассортименту товаров по сравнению с базисным периодом в среднем на 45,5%.
Литература
1. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник/А.И. Харламов, О.Э. Башина, В.Т. Бабурин и др.; Под ред. А.А. Спирина, О.Э.Башиной – 4-е изд. – М.: Финансы и статистика, 1997.
2. Статистика: Учебник/ Под ред. Проф. И.И. Елисеевой – М.: ООО «Витрэм», 2002.
3. Практикум по теории статистики: Учебное пособие/ Под ред. Проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2001.
4. Теория статистики: Учебник/ Под ред. Проф. Р.А. Шмойловой. – 3-е изд., перераб. – М.: Финансы и статистика, 2001.
5. Экономическая статистика: Учебник/ Под ред. Ю.Н. Иванова. – М.: ИНФРА-М, 1998.
6. Ефимова М.Р., Ганченко О.И., Петрова Е.В. Практикум по общей теории статистики: Учебное пособие. – М.: Финансы и статистика, 2000.
7. Статистика. Пособие студентам для подготовки к экзаменам. Издательско-торговая компания «Дашков и К», М.: 2004
8. Шмойлова Р.А., Минашкина В.Г., Садовникова Н.А.Практикум по теории статистики. М.: «Финансы и статистика», 2004
9. Общая теория статистики: учеб. для студ. вузов / М. Р. Ефимова, Е. В. Петрова, В. Н. Румянцев. - 2-е изд., испр. и доп. - М. : ИФРА-М, 2007.
Дата добавления: 2021-09-25; просмотров: 648;











