Тема 8. Ряды динамики
1.Понятие рядов динамика, их виды
2. Показатели рядов динамики
3. Средние показатели рядов динамики
1.Основная цель статистического изучения динамики развития социально-экономических явлений состоит в выявлении и измерении закономерностей их развития во времени. Это достигается посредством, построения и анализа статистических рядов динамики.
Ряды динамики – числовые значения определенного стат. показателя в последовательные моменты или периоды времени.
В каждом ряду динамики имеются два основных элемента:
1) показатель времени t;
2) соответствующие им уровни развития изучаемого явления у.
Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или среднимивеличинами.
В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты) времени, либо отдельные периоды (годы, кварталы, месяцы, сутки).
В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на моментные и интервальные.
Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени.
Примером моментного ряда динамики является следующая информация о списочной численности работников магазина в 2013 г.:
| Дата | 01.01.2013 | 01.04.2013 | 01.07.2013 | 01.10.2013 | 01.01.2014 |
| Число работников, чел. |
Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Так, основная часть персонала магазина, составляющая списочную численность на 01.01.2013 г., продолжающая работать в течение данного года, отображена в уровнях последующих периодов. Поэтому при суммировании уровней моментного ряда динамики может возникнуть повторный счет.
Посредством моментных рядов динамики в торговле изучают товарные запасы, состояние кадров, количество оборудования и других показателей, отображающих состояние изучаемых явлений на отдельные даты (моменты) времени.
Интервальные ряды динамики отображают итоги развития изучаемых явлений за отдельные периоды (интервалы) времени.
Примером интервального ряда динамики могут служить данные о розничном товарообороте магазина в 2010-2014 гг.:
| Год | |||||
| Объем розничного товарооборота, тыс. руб. | 885,7 | 932,6 | 980,1 | 1028,7 | 1088,4 |
Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы (субпериоды) времени. Например, суммируя товарооборот за первые три месяца года, получают его объем за I квартал, а сумма товарооборота четырех кварталов дает объем товарооборота за год и т. д.
Свойство суммирования уровней за последовательные интервалы времени позволяет получать ряды динамики более укрупненных периодов.
Посредством интервальных рядов динамики в торговле изучается изменение во времени поступления и реализации товаров, суммы издержек обращения и других показателей, отображающих итоги функционирования (развития) изучаемых явлений за отдельные периоды.
Основным условием для получения правильных выводов при анализе рядов динамики является сопоставимость его элементов.
Ряды динамики формируются в результате сводки и обработки материалов периодического наблюдения. Повторяющиеся во времени (по отчетным периодам) значения одноименных показателей в ходе статистической сводки систематизируются в хронологической последовательности.
При этом каждый ряд динамики охватывает отдельные обособленные периоды, в которых могут происходить изменения, приводящие к несопоставимости отчетных данных с данными других периодов. Поэтому для анализа ряда динамики необходимо приведение всех составляющих его элементов к сопоставимому виду. Для этого в соответствии с задачами исследования устанавливаются причины, обусловившие несопоставимость анализируемой информации, и применяется соответствующая обработка, позволяющая производить сравнение уровней ряда динамики.
2.Для количественной оценки динамики социально-экономических явлений применяются следующие показатели:
- абсолютные приросты,
- темпы роста и прироста,
- темпы наращивания и др.
В основе расчета показателей рядов динамики лежит сравнение его уровней. В зависимости от применяемого способа сопоставления показатели динамики могут вычисляться на постоянной и переменной базах сравнения.
Для расчета показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными. Для расчета показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели динамики называются цепными.
Важнейшим статистическим показателем динамики является абсолютный прирост, который определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации.
Базисный абсолютный прирост 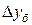 исчисляется как разность между сравниваемым уровнем
исчисляется как разность между сравниваемым уровнем 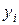 ; и уровнем, принятым за постоянную базу сравнения
; и уровнем, принятым за постоянную базу сравнения 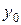 :
:
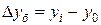 .
.
Цепной абсолютный прирост 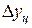 – разность между сравниваемым уровнем
– разность между сравниваемым уровнем 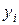 и уровнем, который ему предшествует,
и уровнем, который ему предшествует, 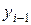 :
:
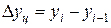 .
.
Абсолютный прирост может иметь и отрицательный знак, показывающий, насколько уровень изучаемого периода ниже базисного.
Между базисными и цепными абсолютными приростамиимеется связь: сумма цепных абсолютных приростов 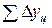 равна базисному абсолютному приросту последнего периода ряда динамики
равна базисному абсолютному приросту последнего периода ряда динамики 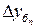 :
:
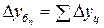 .
.
Распространенным статистическим показателем динамики является темп роста. Он характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах. Базисные темпы роста 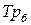 исчисляются делением сравниваемого уровня на уровень, принятый за постоянную базу сравнения,
исчисляются делением сравниваемого уровня на уровень, принятый за постоянную базу сравнения, 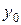 :
:
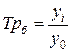 .
.
Цепные темпы роста 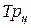 исчисляются делением сравниваемого уровня
исчисляются делением сравниваемого уровня 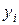 на предыдущий уровень
на предыдущий уровень 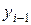 :
:
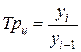 .
.
Если темп роста больше единицы (или 100%), то это показывает на увеличение изучаемого уровня по сравнению с базисным. Темп роста, равный единице (или 100%), показывает, что уровень изучаемого периода по сравнению с базисным не изменился. Темп роста меньше единицы (или 100%) показывает на уменьшение уровня изучаемого периода по сравнению с базисным. Темп роста всегда имеет положительный знак.
Между базисными и цепными темпами роста имеется взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.
Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.
Базисный темп прироста 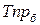 вычисляется делением сравниваемого базисного абсолютного прироста, на уровень, принятый за постоянную базу сравнения.
вычисляется делением сравниваемого базисного абсолютного прироста, на уровень, принятый за постоянную базу сравнения.
Цепной темп прироста 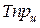 – это отношение сравниваемого цепного абсолютного прироста к предыдущему уровню:
– это отношение сравниваемого цепного абсолютного прироста к предыдущему уровню:
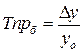 или
или 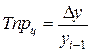
Между показателями темпа прироста и темпа роста имеется взаимосвязь: 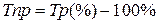 (при выражении темпа роста в процентах) или
(при выражении темпа роста в процентах) или 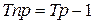 (при выражении темпа роста в коэффициентах). Последние две формулы дают 2-й способ вычисления темпа прироста.
(при выражении темпа роста в коэффициентах). Последние две формулы дают 2-й способ вычисления темпа прироста.
Абсолютное значение 1% прироста – это отношение абсолютного прироста к темпу прироста:
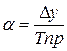 или (2-й способ)
или (2-й способ) 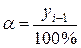 .
.
Пример. Динамика производства продукции промышленного предприятия за 1985 – 1990 г.г.
| Годы | Производство продукции в сопоставимых ценах, млн.руб | Абсолютный прирост, млн. руб | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста, млн.руб. | |||
| Цепной | Базовый | Цепной | Базовый | Цепной | Базовый | |||
| 18,0 | ||||||||
| 19,0 | 1,0 | 1,0 | 105,6 | 105,6 | 5,5 | 5,5 | 0,18 | |
| 20,5 | 1,5 | 2,5 | 107,9 | 113,9 | 7,9 | 13,9 | 0,19 | |
| 21,5 | 1,0 | 3,5 | 104,9 | 119,4 | 4,9 | 19,4 | 0,21 | |
| 23,0 | 1,5 | 5,0 | 106,9 | 127,8 | 6,9 | 27,8 | 0,22 | |
| 25,0 | 2,0 | 7,0 | 108,7 | 138,9 | 8,7 | 38,9 | 0,23 |
3. Средние показатели ряда:
Средний уровень ряда динамики характеризует типическую величину абсолютных уровней.
В интервальных рядах динамики средний уровень определяется делением суммы уровней на их число:
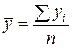 .
.
В моментном ряду динамики с равностоящими датами времени средний уровень определяется по формуле средней хронологической:
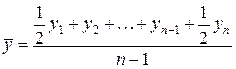
У нас в примере ряд интервальный, следовательно:
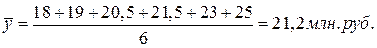
Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. Для определения среднего абсолютного прироста сумма цепных абсолютных приростов делится на их число:
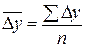 .
.
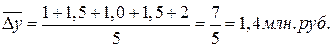
Средний темп роста– обобщающая характеристика индивидуальных темпов роста ряда динамики. Для определения среднего темпа роста применяется формула средней геометрической из показателей коэффициентов роста:
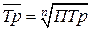 , где
, где 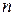 – число темпов роста, или
– число темпов роста, или
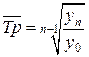 , где
, где 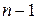 – число уровней ряда, уменьшенное на 1.
– число уровней ряда, уменьшенное на 1.
1) 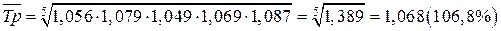 ,
,
2) 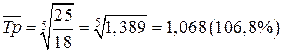 .
.
Средний темп прироста можно определить на основе взаимосвязи между темпами роста и прироста. При наличии данных о средних темпах роста для получения средних темпов прироста используется зависимость:
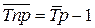 (при выражении среднего темпа роста в коэффициентах),
(при выражении среднего темпа роста в коэффициентах),
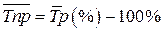 (при выражении среднего темпа роста в процентах).
(при выражении среднего темпа роста в процентах).
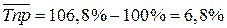 .
.
Среднее абсолютное содержание 1% прироста вычисляется делением суммы значений абсолютного содержания 1% прироста на их число:
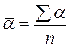 .
.
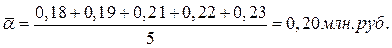
Графически ряды динамики могут быть представлены в виде линейного графика, диаграммы, структурной диаграммы, картограммы, картосхемы.

Задача
Численность рабочих предприятия по месяцам года характеризуются следующими данными (чел.):
на 01.01 2150
на 01.02 2130
на 01.03 2156
на 01.04 2160
на 01.05 2154
на 01.06 2168
на 01.07 2180
на 01.08 2205
Известно, что среднесписочная численность рабочих за III квартал составила 2172 чел., за IV квартал – 2181 чел.
Определите среднесписочную численность рабочих за I-е полугодие, за II-е полугодие и за год в целом.
Решение: Т.к. приведен моментный ряд, расчет производится по средней хронологической:
За I-е полугодие:
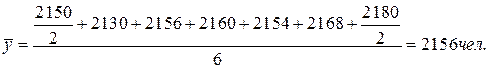
По кварталам:
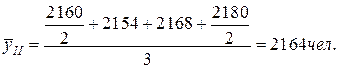
За II-е полугодие: 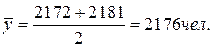
За год: 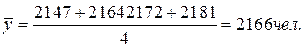
Задача
Ежегодный прирост продукции промышленного предприятия за 2010-2014 г.г. характеризуется следующими данными (в % к предыдущему году):
| 2010 | 2011 | 2012 | 2013 | 2014 |
Исчислите базисные темпы роста (2010 = 100) пр-ва продукции за эти годы и среднегодовой темп роста.
Решение:
Т.к. 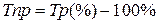 , то темпы прироста составят соответственно: (см. таблицу). Затем воспользуемся формулой, что произведение цепных темпов равно базисную, предварительно сделав базисным 2010 год.
, то темпы прироста составят соответственно: (см. таблицу). Затем воспользуемся формулой, что произведение цепных темпов равно базисную, предварительно сделав базисным 2010 год.
| 2010 | 2011 | 2012 | 2013 | 2014 | |
| прирост цепной | |||||
| рост цепной | |||||
| 100,0 | 106,0 | 111,3 | 119,1 | 128,6 | рост базисный |
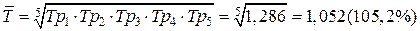 .
.
Дата добавления: 2021-09-25; просмотров: 606;











