Синтаксические меры информации

Объем данных в сообщении измеряется количеством символов (разрядов) принятого алфавита в этом сообщении. Часто информация кодируется числовыми кодами в той или иной системе счисления. Естественно, что одно и то же количество разрядов в разных системах счисления способно передать разное число состояний отображаемого объекта. Действительно, N = mⁿ, где N— число всевозможных отображаемых состояний; m— основание системы счисления (разнообразие символов, применяемых в алфавите); n— число разрядов (символов) в сообщении. В различных системах счисления один разряд имеет различный вес, и соответственно, меняется единица измерения данных. Так, в двоичной системе счисления единицей измерения служит бит (binary digit, двоичный разряд), в десятичной системе счисления — дит (десятичный разряд).

Примечание

Сообщение, представленное в двоичной системе как 10111011, имеет объем данных Vд=8 бит; Сообщение 275903, представленное в десятичной системе имеет объем данных Vд=6 дит. Объем данных в сообщении не зависит от свойств получателя. Для всех получателей он имеет одинаковую величину.

В современных компьютерах наряду с минимальной единицей данных — битом, широко используется укрупненная единица измерения байт, равная 8 бит.

Для определения количества информации Клод Шеннон использовал понятие информационной неопределенности состояния (информационной энтропии) системы. Действительно, получение информации связано с изменением степени неосведомленности получателя о состоянии системы. До получения информации получатель мог иметь некоторые предварительные (априорные) сведения о системе a; мера неосведомленности о системе — Н(a) и является для него мерой неопределенности состояния системы. После получения некоторого сообщения b получатель приобрел дополнительную информацию I_b(a), уменьшившую его априорную неосведомленность так, что апостериорная (после получения сообщения b) неопределенность состояния системы стала Н(a/b). Тогда, количество информации I_b(a) о системе a, полученное в сообщении b, будет определено как: I_b(a) = Н(a) – Н(a/b).

Количество информации измеряется через изменение (уменьшение) неопределенности состояния системы. Если конечная неопределенность Н(a/b) обратится в нуль, то первоначальное неполное знание заменится полным знанием и количество информации станет равно: I_b(a) = Н(a). Иными словами, энтропия системы Н(a) может рассматриваться как мера недостающей информации. Энтропия системы Н(a), имеющей N возможных состояний, согласно формуле Шеннона равна:

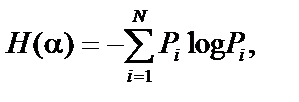
где P_i — вероятность того, что система находится в i-м состоянии.

Для случая, когда все состояния системы равновероятны, то есть
P_i =1/N, энтропия системы: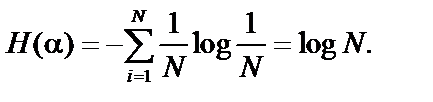

Рассмотрим пример. По каналу связи передается n-разрядное сообщение, использующее m различных символов. Количество всевозможных кодовых комбинаций будет N = mⁿ. При равновероятном появлении любой кодовой комбинации количество информации в правильном сообщении — формула Хартли:

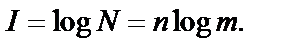
Если в качестве основания логарифма принять m, то I=n. В данном случае количество информации (при условии полного априорного незнания получателем содержания сообщения) будет равно объему данных I=V_д.

Наиболее часто используются двоичные и десятичные логарифмы. Единицами измерения в этих случаях будут соответственно бит и дит.

Для неравновероятных состояний системы всегда:

I <V_д,

Примечание

Меру Шеннона нельзя считать чисто синтаксической мерой, поскольку эта мера зависит от свойств получателя (от вероятностей P_i, значения которых у разных получателей могут быть различными). Более правильно считать меру Шеннона полусемантической мерой количества информации.

Степень информативности сообщения Y определяется отношением количества информации к объему данных, то есть Y = I/V_д, причем 0<Y<1 (Y характеризует лаконичность сообщения). С увеличением Y уменьшаются объемы работы по преобразованию информации (данных) в системе. Для повышения информативности сообщений разрабатываются специальные методы оптимального кодирования информации.