Вставка нового элемента

Для того чтобы вставить новый элемент в дерево, необходимо найти для него место. Для этого, начиная с корня, сравниваем значения узлов (Tree->info) со значением нового элемента (b). Если b < info, то идем по левой ветви, в противном случае – по правой ветви. Когда дойдем до узла, из которого не выходит нужная ветвь для дальнейшего поиска, это означает, что место под новый элемент найдено.

Путь поиска места в построенном дереве для числа 11:

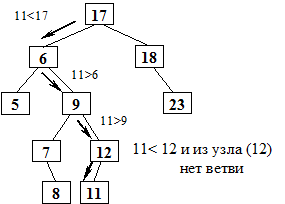
Функция создания дерева, ключами которого являются целые положительные числа, может иметь следующий вид:

Tree* Make(Tree *Root) {

Tree *Prev, *t; // Prev родитель (предыдущий) текущего элемента

int b, find;

if ( Root == NULL ) { // Если дерево не создано

printf("\n Input Root : ");

scanf(“%d”, &b);

Root = List(b); // Установили указатель на корень

}

//================ Добавление элементов =================

while(1) {

printf("\n Input Info : "); scanf(“%d”, &b);

if (b<0) break; // Признак выхода число < 0

t = Root; // Текущий указатель на корень

find = 0; // Признак поиска

while ( t && ! find) {

Prev = t;

if( b == t->info)

find = 1; // Ключи должны быть уникальны

else

if ( b < t -> info ) t = t -> Left;

else t = t -> Right;

}

if (!find) { // Нашли место с адресом Prev

t = List(b); // Создаем новый узел

if ( b < Prev -> info ) // и присоединяем его, либо

Prev -> Left = t; // на левую ветвь,

else Prev -> Right = t; // либо на правую ветвь

}

} // Конец цикла

return Root;

}

Функция List предназначена для создания нового элемента – листа:

Tree* List(int i) {

Tree *t = (Tree*) malloc (sizeof(Tree));

t -> info = i;

t -> Left = t -> Right = NULL;

return t;

}

Участок кода с обращением к функции Create будет иметь следующий вид:

¼

struct Tree { // Декларация шаблона

int info;

Tree *Left, *Right;

};

void main()

{

Tree *Root = NULL; // Указатель корня

¼

Root = Make(Root);

¼

Удаление узла

При удалении узла из дерева возможны три ситуации в зависимости от того, сколько сыновей (потомков) имеет удаляемый узел.

1. Удаляемый узел является листом – просто удаляем ссылку на него. Приведем пример схемы удаления листа с ключом key:

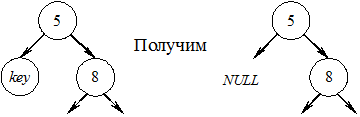
2. Удаляемый узел имеет только одного потомка, т.е. из удаляемого узла выходит ровно одна ветвь. Пример схемы удаления узла key, имеющего одного сына:

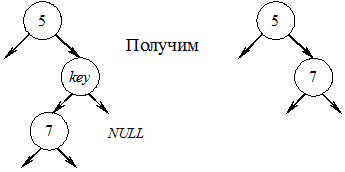
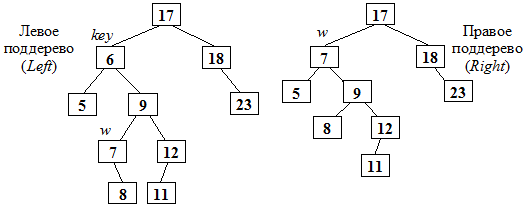
3. Удаление узла, имеющего двух сыновей, значительно сложнее рассмотренных выше. Если key – удаляемый узел, то его следует заменить узлом w, который содержит либо наибольший ключ (самый правый, у которого указатель Right равен NULL) в левом поддереве, либо наименьший ключ (самый левый, у которого указатель Left равен NULL) в правом поддереве.

Используя первое условие, находим узел w, который является самым правым узлом поддерева key, у него имеется только левый сын:

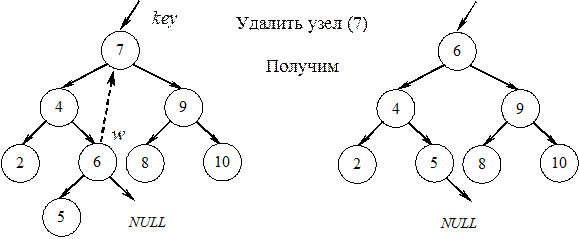
В построенном ранее дереве удалим узел key (6). Используем второе условие, т.е. ищем самый левый узел в правом поддереве – это узел w (указатель Left равен NULL):

Функция удаления узла по заданному ключу key может иметь вид

Tree* Del(Tree *Root, int key) {

Tree *Del, *Prev_Del, *R, *Prev_R;

// Del, Prev_Del – удаляемый элемент и его предыдущий (родитель);

// R, Prev_R – элемент, на который заменяется удаленный, и его родитель;

Del = Root;

Prev_Del = NULL;

// ===== Поиск удаляемого элемента и его родителя по ключу key =====

while (Del != NULL && Del -> info != key) {

Prev_Del = Del;

if (Del->info > key) Del = Del->Left;

else Del = Del->Right;

}

if (Del == NULL) { // Элемент не найден

puts("\n NO Key!");

return Root;

}

// ============ Поиск элемента R для замены =================

if (Del -> Right == NULL) R = Del->Left;

else

if (Del -> Left == NULL) R = Del->Right;

else {

// Ищем самый правый узел в левом поддереве

Prev_R = Del;

R = Del->Left;

while (R->Right != NULL) {

Prev_R = R;

R = R->Right;

}

// Нашли элемент для замены R и его родителя Prev_R

if( Prev_R == Del)

R->Right = Del->Right;

else {

R->Right = Del->Right;

Prev_R->Right = R->Left;

R->Left = Prev_R;

}

}

if (Del== Root) Root = R; // Удаляя корень, заменяем его на R

else

// Поддерево R присоединяем к родителю удаляемого узла

if (Del->info < Prev_Del->info) Prev_Del->Left = R; // на левую ветвь

else Prev_Del->Right = R; // на правую ветвь

printf("\n Delete element %d \n", Del->info);

free(Del);

return Root;

}

Участок программы с обращением к данной функции будет иметь вид

¼

printf("\n Input Del Info : ");

scanf(“%d”, &key);

Root = Del(Root, key);

¼