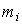Проверка нормальности распределения результатов наблюдений
Результаты наблюдений можно оценить наиболее полно, если их распределение является нормальным. Поэтому исключительно важную роль при обработке результатов наблюдений играет проверка нормальности распределения.
Эта задача представляет собой частный случай более общей проблемы, заключающейся в подборе теоретической функции распределения, в некотором смысле наилучшим образом согласующейся с опытными данными.
При большом числе результатов наблюдений (n>40) данная задача решается в следующем порядке.
Весь диапазон полученных результатов наблюдений Xmax ... Xmin разделяют на r интервалов шириной 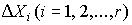 и подсчитывают частоты mi, равные числу результатов, лежащих в каждом i-м интервале, т. е. меньших или равных его правой и больших левой границы.
и подсчитывают частоты mi, равные числу результатов, лежащих в каждом i-м интервале, т. е. меньших или равных его правой и больших левой границы.
Отношения
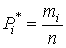
|
где n - общее число наблюдений, называются частостями и представляют собой статистические оценки вероятностей попадания результата наблюдений в i-й интервал. Распределение частот по интервалам образует статистическое распределение результатов наблюдений.
Если теперь разделить частость на длину интервала, то получим величины
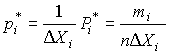
|
являющиеся оценками средней плотности распределения в интервале 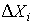 .
.
Отложим вдоль оси результатов наблюдений (рис.11) интервалы  в порядке возрастания индекса i и на каждом интервале построим прямоугольник с высотой, равной
в порядке возрастания индекса i и на каждом интервале построим прямоугольник с высотой, равной 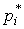 . Полученный график называется гистограммой статистического распределения.
. Полученный график называется гистограммой статистического распределения.
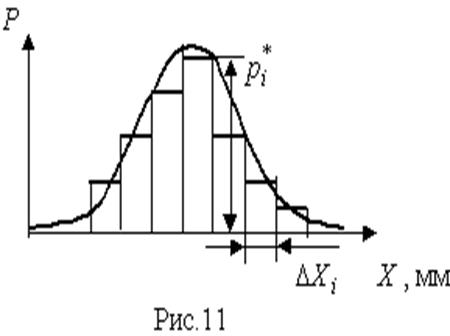
Площадь суммы всех прямоугольников равна единице:
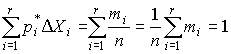
При увеличении числа наблюдений число интервалов можно увеличить. Сами интервалы уменьшаются, и гистограмма все больше приближается к плавной кривой, ограничивающей единичную площадь, - к графику плотности распределения результатов наблюдений.
При построении гистограмм рекомендуется пользоваться следующими правилами:
1. Число интервалов выбирается в зависимости от числа наблюдений согласно рекомендациям табл.3.
Таблица 3
|
2. Длины интервалов удобнее выбирать одинаковыми. Однако если распределение крайне неравномерно, то в области максимальной концентрации результатов наблюдений следует выбирать более узкие интервалы.
3. Масштабы по осям гистограммы должны быть такими, чтобы отношение ее высоты к основанию составляло примерно 5:8.
Пример. Было выполнено 100 измерений среднего диаметра резьбового калибра. Результаты наблюдений лежат в диапазоне 8.911 - 8.927 мм, т. е. зона распределения результатов составляет 0.016 мм. Весь диапазон удобно разделить на восемь равных интервалов через 0.002 мм. В табл.4 приведены частоты mi, частости 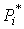 и плотности
и плотности 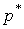 статистического распределения.
статистического распределения.
Таблица 4
|
После построения гистограммы надо подобрать теоретическую плавную кривую распределения, которая, выражая все существенные черты статистического распределения, сглаживала бы все случайности, связанные с недостаточным объемом экспериментальных данных. Принципиальный вид теоретической кривой выбирают заранее, проанализировав метод измерения, или хотя бы по внешнему виду гистограммы. Тогда определение аналитического вида кривой распределения сводится к выбору таких значений его параметров, при которых достигается наибольшее соответствие между теоретическим и статистическим распределением. Одним из методов решения этой задачи является метод моментов. При его использовании параметрам теоретического распределения придают такие значения, при которых несколько важнейших моментов совпадают с их статистическими оценками. Так, если статистическое распределение, определяемое гистограммой, приведенной на рис.11, мы хотим описать кривой нормального распределения, то естественно потребовать, чтобы математическое ожидание и дисперсия последнего совпадали со средним арифметическим и оценкой дисперсий, вычисленным по опытным данным. В предыдущем примере 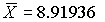 мм,
мм, 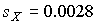 мм и уравнение кривой нормального распределения, лучше всего согласующегося со статистическим распределением, должно иметь вид:
мм и уравнение кривой нормального распределения, лучше всего согласующегося со статистическим распределением, должно иметь вид:
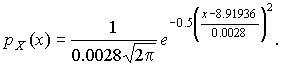
Далее законно возникает вопрос, объясняются ли расхождения между гистограммой и подобранным теоретическим распределением только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они вызваны тем, что результаты наблюдений в действительности распределены иначе?
Для ответа на этот вопрос используют методы проверки статистических гипотез. Идея их применения заключается в следующем. На основании гистограммы, полученной при обработке опытных данных, строится гипотеза, состоящая в том, что результаты наблюдений подчиняются распределению 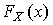 с плотностью
с плотностью 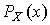 .
.
Для того чтобы принять или опровергнуть эту гипотезу, выбирается некоторая величина U, представляющая собой меру расхождения теоретического и статистического распределений. В качестве меры расхождения можно принять сумму квадратов разностей частостей и теоретических вероятностей попадания результатов наблюдений в каждый интервал, взятых с некоторыми коэффициентами:
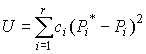 , ,
|
где  – коэффициенты, называемые весами разрядов;
– коэффициенты, называемые весами разрядов;  – теоретические вероятности, определяемые как
– теоретические вероятности, определяемые как
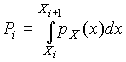 , ,
|
Здесь  – предполагаемая плотность распределения.
– предполагаемая плотность распределения.
Мера расхождения U является случайной величиной и, независимо от исходного распределения подчиняется 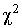 -распределению с k степенями свободы. Если значения всех частот
-распределению с k степенями свободы. Если значения всех частот 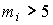 , число измерений стремится к бесконечности, а веса
, число измерений стремится к бесконечности, а веса 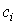 выбираются равными
выбираются равными 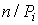 . Число степеней свободы распределения k = r - s, где
. Число степеней свободы распределения k = r - s, где 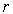 – число разрядов гистограммы статистического распределения, а s – число независимых связей, наложенных на частости
– число разрядов гистограммы статистического распределения, а s – число независимых связей, наложенных на частости 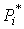 .
.
Систематическая погрешность – составляющая погрешности, которая остаётся постоянной при повторных измерениях одной и той же величины.
Причины возникновения систематической погрешности:
- неисправность измерительного устройства;
- несовершенство метода измерения;
- неправильная установка измерительного устройства;
- отступление условий эксплуатации от нормальных;
- особенности оператора производимого измерения;
- и др.
Инструментальная погрешность – составляющая погрешности измерения, зависящая от погрешностей применяемых средств измерений, т.е. обусловлена особенностью конструкции измерительного устройства, неточностью градуировки, шкалы, а также неправильностью установки измерительного устройства. Инструментальная погрешность, как правило, указывается в паспорте на средство измерения и может быть оценена в числовом выражении.
Методическая погрешность – обусловлена несовершенством применяемого метода измерения , неточностью формул и математических зависимостей, описывающий данный метод измерения, а также влиянием средства измерения на объект свойства которого изменяются.
Грубая погрешность измерения - погрешность измерения, существенно превышающая ожидаемую при данных условиях погрешность.
Погрешность отсчитывания - составляющая погрешности измерения, происходящая от недостаточно точного отсчитывания показаний средства измерений.
Систематическая погрешность измерения - составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины.
Примеры. Погрешность от несоответствия действительного значения меры, с помощью которой выполняют измерения, ее номинальному значению; погрешность вследствие постепенного уменьшения силы рабочего тока в цепи электроизмерительного потенциометра.
Систематическая погрешность может быть выявлена и устранена путём анализа возможных источников её возникновения в каждом конкретном случае.
Субъективная погрешность обусловлена несоответствием органов зрения оператора производимого измерение (косоглазие). Для устранения этой погрешности все измеряемые устройства снабжают дополнительными шкалами (зеркальными).
Все системные погрешности классифицируются на две группы:
- постоянные (проще всего устраняются путём коррекции показаний с помощью корректора);
- закономерно изменяющиеся:
1) прогрессирующие;
2) периодические;
3) изменяются по сложному закону.
Причинами возникновения закономерно изменяющихся погрешностей являются – колебания в широком диапазоне, изменение параметров окружающей среды (температура, влажность, запылённость и так далее), а также изменение других влияющих величин по сложному законы.
Прогрессирующие погрешности являются сложными и непредсказуемыми, так как могут либо возрастать, либо убывать в отличии от периодической погрешности, которая появляется и исчезает с каким либо периодом.
Методы устранения систематической погрешности могут быть разбиты на основные и специальные.
К основным относятся:
1) термостабилизация;
2) термоизоляция;
3) установка специальных экранов защищающих от действия внешних полей;
4) использование в конструкциях средств измерения амортизирующих устройств;
5) применение стабилизаторов питающего напряжения и др.
К специальным методам устранения системной погрешности относятся:
1) метод замещения, при котором измеряемая величина заменяется известной величиной, таким образом, что составление и действие ИП остаётся неизменным, а измерение при этом производится дважды;
2) метод противопоставления, при этом методе измеряемая величина заменяется (противопоставляется) известной величиной задаваемой мерой;
3) метод компенсации погрешности по знаку – обычно применяется, когда имеет место направляемая или знакочередующая погрешность.
4) метод постоянных наблюдений – в соответствии с этим методом измерение физической величины и оценка системной погрешности производится трижды, с использованием образцовой меры на входе измеряемого устройства;
5) метод периодических наблюдений – применяется в случае периодической составляющей системной погрешности и направлен на её устранение.
Систематическую погрешность, как правило, полностью устранить не представляется возможным, однако если известна функциональная зависимость влияющей величины от других факторов, то эта составляющая погрешности может быть оценена и оставаться достаточно маленькой.
Случайная погрешность – составляющая погрешности, которая изменяется случайным образом при повторных измерениях одной и той же величины. Причиной случайной погрешности является одновременное действие многих случайных факторов, каждый из которых в отдельности мало влияет.
Примеры. Погрешность вследствие вариации показаний измерительного прибоpa; погрешность округления при отсчитывании показаний измерительного прибора.
В ряде измерений результат одного отдельно взятого измерения может резко отличатся от результатов других измерений из-за ошибок оператора, толчков, действия сильных помех, изменение электрического контакта и других причин. Этот результат следует отнести к грубым промахам и исключить из дальнейшей статической обработки.
Промахи – это грубые ошибки, например, ошиблись при записи показаний прибора (вместо 10,2 записали 102 или 202), неправильно приложили начало линейки к измеряемому объекту, промахи обусловлены, как правило, недостатком внимания и аккуратности исследователя.
Случайная погрешность может быть оценена и частично снижена путём правильной обработки методами математической статистики, а также методами вероятности.
Аддитивная погрешность – погрешность измерения, которая при всех значениях входной измеряемой величины Х приводит к изменению значения выходной величины У на одну и ту же величину большую или меньшую от номинального значения.
Причиной возникновения мультипликативной погрешности является изменение коэффициента усиления усилителя, изменение коэффициента деления делителя напряжения и другие причины.
Все погрешности СИ классифицируются на: основные погрешности СИ, которые имеют место и характеризуются нормальными условиями эксплуатации измеряемого устройства (нормальное относительное давление, температура, влажность и другие причины).
Дополнительные погрешности имеют место в условиях эксплуатации, в условиях, отличающихся от нормальных по давлению, влажности, температуре и других. В зависимости от изменения входного сигнала во времени все погрешности СИ классифицируются на: статическую погрешность – не зависит от скорости изменения измеряемой величины во времени (состояние СИ при котором значения входных и выходных сигналов не изменяется во времени).
Аддитивная 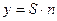 Мультипликативная
Мультипликативная 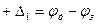
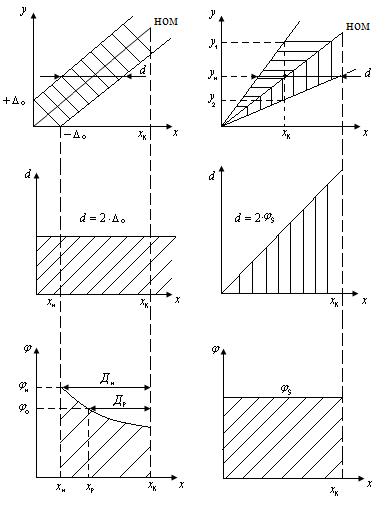
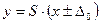
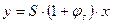
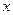 - измеряемая величина;
- измеряемая величина;
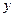 `- выходная величина;
`- выходная величина;
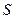 - чувствительность;
- чувствительность;
 - относительная погрешность чувствительности;
- относительная погрешность чувствительности;
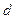 - интервал неопределённости;
- интервал неопределённости;
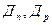 - полный и рабочий диапазоны измерения;
- полный и рабочий диапазоны измерения;
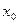 - начальное значение измеряемой величины;
- начальное значение измеряемой величины;
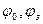 - начальное и заданное значения относительной погрешности;
- начальное и заданное значения относительной погрешности;
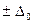 - абсолютная погрешность нуля (аддитивная погрешность).
- абсолютная погрешность нуля (аддитивная погрешность).
Динамическая погрешность средства измерений - разность между погрешностью средства измерений в динамическом режиме и его статической погрешностью, соответствующей значению величины в данный момент времени.
В ряде измеряемых устройств существует погрешность гистерезиса (запаздывание), погрешность обратного хода. Является наиболее существенной и трудно устранимой погрешностью, которая выражается в виде реальной функции преобразования.

Причины погрешности гистерезиса:
1) наличие люфта в механических передающих элементах;
2) сухое трение (в керновых узлах);
3) упругое последействие в упругих чувствительных элементах;
4) явление поляризации в пьезоматериалах.
Абсолютная погрешность – погрешность измерения, выраженная в единицах измеряемой величины. Эта погрешность может задаваться в единицах измеряемой величины; в виде уравнения; с помощью таблиц.
Относительная погрешность – отношение абсолютной погрешности к значению измеряемой величины, выраженному в процентах.
1) 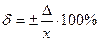
2) С помощью уравнения прямой:
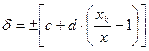 , где
, где
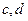 - постоянные коэффициенты, определяющие положение измеряемой величины.
- постоянные коэффициенты, определяющие положение измеряемой величины.
Xk – конечное значение измеряемой величины по диапазону 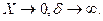
Приведенная погрешность – отношение абсолютной погрешности к нормированному значению измеряемой величины:
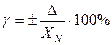
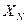 - нормированное значение измеряемой величины. В его качестве принимается для приборов имеющих одностороннюю, равномерную или степенную шкалу, конечное значение по шкале для приборов с двухсторонней шкалой и с 0 по середине принимается сумма конечных значений.
- нормированное значение измеряемой величины. В его качестве принимается для приборов имеющих одностороннюю, равномерную или степенную шкалу, конечное значение по шкале для приборов с двухсторонней шкалой и с 0 по середине принимается сумма конечных значений.
Дата добавления: 2021-09-25; просмотров: 446;

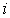
 , мм
, мм
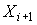 , мм
, мм