Трение в механизмах
Трение скольжения
Трение скольжения возникает между соприкасающимися между собой и сдвигающимися друг относительно друга телами. Наиболее часто его объясняют наличием микронеровностей и шероховатостей на трущихся поверхностях. Различают сухое трение (поверхности контактируют непосредственно), полусухое или полужидкостное трение (поверхности частично разделены слоем смазки), жидкостное трение (слой смазки полностью разделяет трущиеся поверхности). При жидкостном трении сопротивление движению создается не взаимодействием трущихся материалов, а взаимодействием отдельных слоев смазочной жидкости, которые прилипают к поверхностям тел и увлекаются ими в противоположных направлениях. В реальных механизмах микронеровности могут прорывать слой смазки из-за высоких давлений, и трение не может быть полностью жидкостным. Для обеспечения жидкостного трения соответствующие поверхности тел должны иметь вполне определенную шероховатость с высокой опорной поверхностью для размещения достаточного объема жидкости. Изучением трения и изнашивания материалов занимается специальная науки - триботехника.
В настоящее время известно два закона трения скольжения: о направлении сил трения и о величине сил трения. Согласно первому закону силы трения возникают попарно, приложенные к обоим телам. Каждая из этих сил направлена в сторону, противоположную скорости относительного движения того тела, к которому она приложена. При отсутствии относительного движения силы трения направлены противоположно тому движению, которое произошло бы в их отсутствие.
Второй закон устанавливает прямопропорциональную зависимость между силой трения и силой нормального давления:
F = f . N.
Где f – коэффициент трения скольжения, безразмерная величина, зависящая от материала и качества трущихся поверхностей, а также от наличия смазки.
Средние значения коэффициента трения составляют:
- чугун по чугуну без смазки 0,22
- сталь по чугуну без смазки 0,16 – 0,18
- сталь по чугуну со смазкой 0,1
- шлифованная сталь по чугуну при обильной смазке 0,01
В момент трогания с места сила трения имеет максимальное значение, называемое трением покоя и равна Fmax = f0 . N,
где f0 > f коэффициент трения покоя.
Трение качения
Если одно из контактирующих тел во время относительного движения перекатывается по другому, то имеет место трение качения.
Пусть неподвижный каток, нагруженный силой Q, лежит на горизонтальной плоскости. Между катком и плоскостью возникает площадка смятия abc, напряжения на которой распределяются по эллиптическому закону (рис. 2-3 ).
Суммарная реакция плоскости N проходит через центр катка и уравновешивает силу Q (рис. 2 а). Если начать перекатывать каток вправо, то участок ab площадки смятия будет находиться в зоне исчезающей деформации, а участок bc – в зоне нарастающей деформации (рис. 2 б). В этом случае напряжения по площадке распределяются несимметрично, а суммарная реакция плоскости N смещается в сторону движения катка на расстояние k и образует вместе с силой Q пару сил, препятствующую движению. Момент этой пары сил называют моментом трения качения Мтрк = k . Q. Величину k называют коэффициентом трения качения.
 Q Q
a b c
|  Q Q
 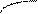  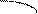   Mтрк Mдв Mтрк Mдв
 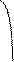 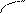  N V N V
a b c
|  Q Q
R
F
| |||||||||||||||
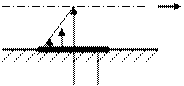
| a | б | Рис. 3 Трение в контакте плоского и круглого тел при условии, что круглое тело - ведомое | |||||||||||||||
| Рис. 2 Площадки контакта и напряжения в них для случаев неподвижного (а) и двигающегося (б) тела качения |
В противоположность скольжению сопротивление качению выражается не силой, а парой сил и коэффициент трения в этом случае имеет размерность длины. Величина коэффициента трения качения значительно меньше, чем для скольжения, например: шарики в подшипнике – 0,001 см, колесо по рельсам – 0,01 см, резиновая шина по грунтовой дороге - 1 см.
Для трения качения необходимо рассмотреть два случая:
- колесо ведущее (к катку необходимо приложить движущий момент Мдв),
- колесо ведомое (к центру катка необходимо приложить движущую силу Р).
Последний случай представлен на рис. 3. Между катком и плоскостью возникает сила трения скольжения F, которая препятствует скольжению катка. Равномерное движение катка будет обеспечено при выполнении условия:
P = (k/R)Q.
Если бы было чистое скольжение, то P = fQ. Поэтому можно сравнивать величины f и k/R. Всегда f > k/R. Отсюда вытекает условие чистого качения ведомого катка: Сила Р, достаточная для перекатывания катка, должна быть меньше максимального значения силы трения скольжения, т.е. P = (k/R) Q < f0 Q, или f0 > k/R.
Угол трения. Понятие о самоторможении
С понятием трения тесно связана величина угла трения. Рассмотрим силу F, приложенную к ползуну, как горизонтальную реакцию плоскости. Если геометрически сложить нормальную реакцию N и силу трения F, то получим полную реакцию плоскости R (рис. 4 ).
R j N
F = f.N
| Она будет отклонена от нормали в сторону, противоположную движению ползуна на величину некоторого угла j, который называют углом трения. Его величина связана с коэффициентом трения соотношением: tg j = f. | |||||||||
| Рис. 4 Схема, поясняющая образование угла трения |
При движении ползуна по наклонной плоскости можно записать условие равномерного подъема и спуска, используя понятие угла трения:
P = Q tg (l + j),
P = Q tg (l - j).
В этих выражениях l – угол наклона плоскости, а для винтовой пары – угол подъема винтовой линии.
Коэффициент полезного действия наклонной плоскости с увеличением l сначала возрастает, а затем начинает убывать. Максимальный к.п.д. обеспечивается при l = 450 - j /2.
В случае спуска ползуна по наклонной плоскости может иметь место случай, когда движения под действием вертикальной силы не происходит, т.е. можно говорить о самоторможении ползуна на плоскости. Условием самоторможения является выражение : l < j . Если это условие не выполняется, то движение ползуна возможно как под действием силы Р, так и под действием силы Q.
Дата добавления: 2017-09-01; просмотров: 1574;


 N V=0
N V=0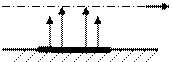

 k
k


 P
P N
N

 k
k