Соотношения для электрических величин на границе раздела двух диэлектриков.

Рассмотрение свойств электростатического поля в неоднородной диэлектрической среде было бы неполным без анализа зависимостей между компонентами соответствующих векторных полей по разные стороны от границы раздела свойств диэлектрика.

Рассмотрим сначала зависимость между нормальными к поверхности раздела компонентами векторного поля 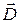. Пусть в окрестности произвольной точки поверхности 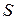раздела двух сред выделена малая площадка 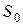и выбрано положительное направление нормали 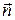. Среда, расположенная в “положительном” пространстве относительно поверхности 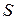, описывается величинами с индексом 2, а среда в “отрицательном” пространстве относительно поверхности 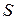, описывается величинами с индексом 1. Из каждой точки контура, ограничивающего площадку 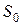, восстановим перпендикуляр к поверхности 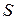и отложим в среде 2 и среде 1 на этом перпендикуляре отрезок . 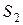Поверхность площадок и 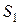вместе с боковой поверхностью 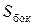(рис. 1) образуют замкнутую поверхность, охватывающую объем с различающимися локальными характеристиками.

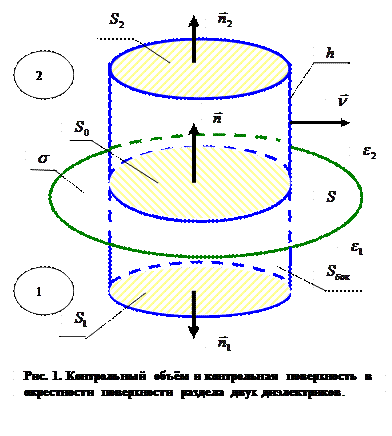
К рассматриваемому объему применима теорема Гаусса для векторного поля 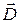в интегральной форме:

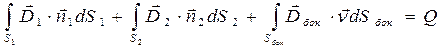, (1)

где - вектор внешней нормали к элементу площади боковой поверхности, 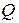- суммарная величина свободных зарядов внутри рассматриваемого объема:

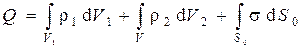. (2)

При записи выражения (2) учтено, что в среде 1 и среде 2 может существовать объемная плотность свободных электрических зарядов, а сама поверхность 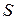может дополнительно содержать свободные заряды с поверхностной плотностью .

В математическом анализе известна оценка максимальной величины интеграла :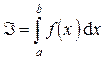

.

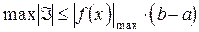С учетом этой оценки можно получить неравенства

При 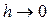эти интегралы стремятся к нулю, площадка 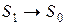, площадка 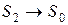, и в итоге получается условие:

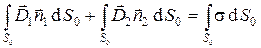. (3)

Замечая, что , приходим к соотношению:

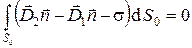. (4)

Поскольку соотношение (4) должно выполняться для произвольной площадки 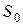, то из интегрального условия (4) следует локальное условие:

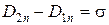. (5)

Сформулируем полученный результат: нормальные компоненты векторного поля 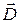на границе раздела двух сред испытывают скачок, равный поверхностной плотности свободных электрических зарядов (если она отлична от нуля).

Соотношение (5) теряет силу для точек поверхности 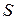, в которых расположены точечные заряды, и для линий, лежащих на поверхности 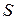и заряженных погонной плотностью свободных зарядов.

Заметим, что теоремы Гаусса для векторных поле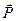й и по форме не отличаются от теоремы Гаусса для поля 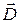, поэтому, в частности, справедливо условие

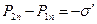, (6)

- поверхностная плотность связанных зарядов, расположенных на поверхности 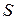раздела двух сред. Поскольку чаще всего эта величина неизвестна, то соотношение (6) используют для ее расчета.

Векторное поле напряженности электростатического поля и в диэлектрической среде остается потенциальным:

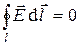. (7)

Действительно, единственным ограничением при выводе условия (7) было требование неподвижности электрических зарядов, формирующих это поле. В условиях электростатики и свободные, и связанные заряды неподвижны, следовательно, условие (7) имеет место.

Напомним вывод локального условия для тангенциальных (касательных) компонент вектора напряженности электростатического поля на границе раздела двух диэлектриков. В окрестности произвольной точки поверхности 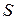раздела двух сред после выбора положительного направления нормали рассмотрим замкнутый контур, показанный на рис. 2.

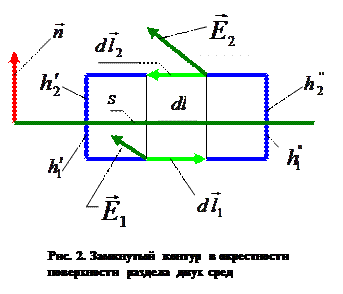
В силу условия (7) получаем

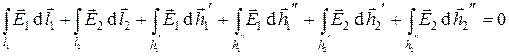
В этом соотношении 4 последних интеграла в левой части пропорциональны величине и при их величины также стремятся к нулю.

В итоге, когда отрезок контура 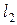“ложится” на отрезок 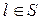, отрезок контура 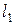“ложится” на отрезок 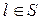, их направления противоположны, получаем интегральное условие

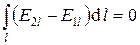, (8)

откуда в силу произвольности отрезка контура 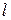получаем условие:

. (9)

Сформулируем полученный результат: тангенциальные (касательные) компоненты векторного поля непрерывны при переходе через границу раздела двух сред. Соотношение справедливо для любого направления, касательного к рассматриваемой поверхности. Для магнитного поля в окрестности поверхности раздела двух сред, как это будет показано ниже, скачок между касательными компонентами напряженности магнитного поля при переходе через границу раздела может зависеть от выбранного направления касательной линии.

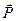Заметим, что касательные компоненты векторного поля однозначно формируют касательные компоненты векторных полей и 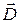, если среды изотропны. Поэтому условия (9) достаточно для получения соотношений связи касательных компонент векторных поле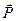й и 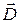на границе раздела двух сред.

На рис. 3 показано поведение компонент векторного поля напряженности и векторного поля электрического смещения на регулярной границе раздела двух диэлектриков для случая отличной от нуля поверхностной плотности свободных электрических зарядов. При этом терпят разрыв нормальные и касательные компоненты вектора электрического смещения и нормальные компоненты вектора напряженности электрического поля. Касательные компоненты вектора напряженности электрического поля являются непрерывными величинами. Легко видеть, что наклон силовых линий и того и другого векторного полей изменяется при переходе через границу раздела диэлектриков.

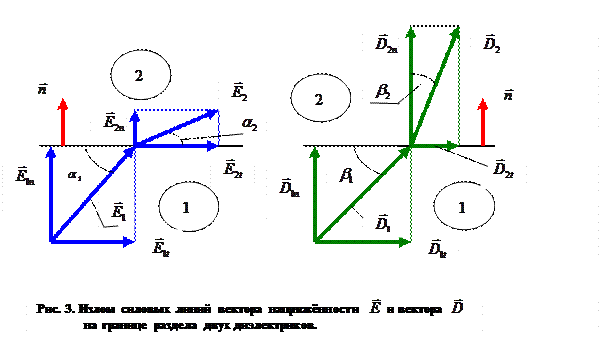
В заключение раздела отметим, что интегральная форма теоремы Гаусса, дифференциальная форма теоремы Гаусса, интегральное и дифференциальное условия потенциальности электростатического поля и соотношения на поверхности раздела сред органически связаны друг с другом и одно немыслимо без другого.