Движение искусственных спутников Земли и космических аппаратов

На основании закона всемирного тяготения Ньютон первым теоретически обосновал возможность создания искусственного спутника Земли. Давайте вспомним, что искусственными спутникаминазывают космические аппараты, созданные людьми, которые позволяют наблюдать за планетой, около которой они вращаются, а также другими астрономическими объектами из космоса.

Чтобы понять, при каких условиях тело способно стать искусственным спутником Земли, обратимся к размышлениям Ньютона. Их суть такова: если бросить с высокой горы камень в горизонтальном направлении, то, двигаясь по ветви параболы, он со временем упадёт на Землю. Сообщив ему большую скорость, он упадёт дальше. Поскольку Земля имеет шарообразную форму, то одновременно с продвижением камня по его траектории поверхность Земли удаляется от него. Значит, можно подобрать такое значение скорости камня, при котором поверхность Земли из-за её кривизны будет удаляться от камня ровно на столько, на сколько камень приближается к Земле под действием силы тяжести. Тогда тело будет двигаться на постоянном расстоянии от поверхности Земли, то есть станет её искусственным спутником.

Так как за пределами атмосферы силы сопротивления движению спутнику отсутствуют, то на него будет действовать только сила притяжения к Земле. Поэтому спутник движется как свободно падающее тело с ускорением свободного падения.

Искусственным спутником Земли может стать любое тело произвольной массы. Важно, чтобы ему сообщили за пределами земной атмосферы горизонтальную скорость, при которой оно начнёт двигаться по окружности вокруг Земли.

Скорость, при достижении которой космический аппарат, запускаемый с Земли, может стать её искусственным спутником, называется первой космической скоростью:

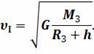
По этой же формуле мы можем рассчитать и первую космическую скорость спутника для любой планеты, заменив в ней радиус и массу Земли на радиус и массу исследуемой планеты.

Вблизи поверхности Земли первую космическую скорость можно определить, как:

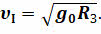
Приняв радиус равным 6371 км, а ускорение свободного падения — 9,8 м/с², получим, что для Земли первая космическая скорость равна 7,9 км/с.

Именно такую скорость в горизонтальном направлении нужно сообщить телу на небольшой, сравнительно с радиусом Земли, высоте, чтобы оно не упало на Землю, а стало её спутником, движущимся по круговой орбите.

Возникает закономерный вопрос: «Почему же тогда свободно падающий спутник не падает на Землю?»

Примем для простоты расчётов, что ускорение свободного падения равно 10 м/с², а скорость спутника — 8 км/с. Тогда за одну секунду свободного падения спутник пройдёт по направлению к Земле 5 метров и одновременно с этим переместиться перпендикулярно этому направлению на 8 километров. В результате этих двух движений спутник и движется по своей орбите.

Так, например, наша Луна уже более 4,5 миллиардов лет обращается вокруг Земли.

Восемь километров в секунду — это почти 29 000 километров в час! Сообщить телу такую скорость, конечно, не просто. Только в 1957 году советским учёным впервые в истории человечества удалось с помощью мощной ракеты сообщить телу массой около 85 килограмм первую космическую скорость, и оно стало первым искусственным спутником Земли.

Если телу сообщить скорость, большую, чем первая космическая на данной высоте, то орбита спутника будет представлять собой эллипс. И чем больше сообщённая телу скорость, тем более вытянутой будет его орбита.

Скорость, при достижении которой космический аппарат, запускаемый с Земли, может преодолеть земное притяжение и осуществить полёт к другим планетам Солнечной системы, называется второй космической скоростью.

Расчёты показывают, что для преодоления земного притяжения скорость космического аппарата должна быть больше первой космической скорости в корень из двух раз (без учёта сопротивления воздуха):

Третья космическая скорость, или гиперболическая скорость, — это наименьшая начальная скорость, с которой тело должно преодолеть земное притяжение и выйти на околосолнечную орбиту со скоростью, необходимой для того, чтобы навсегда покинуть пределы Солнечной системы:

В формуле 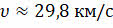— это орбитальная скорость нашей планеты.

Если в это уравнение подставить все известные величины и произвести вычисления, получим, что тело должно иметь минимальную скорость, примерно равную 16,7 км/с, чтобы начать двигаться по гиперболе и покинуть пределы Солнечной системы.

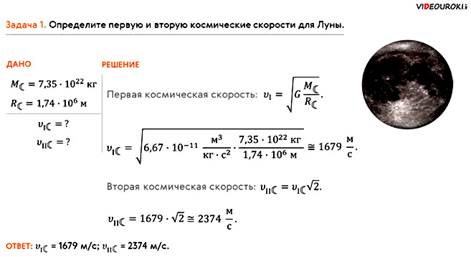
Конечно же, по записанным нами формулам можно рассчитывать космические скорости не только для Земли, но и других тел Солнечной системы. Для примера давайте определим первую и вторую космические скорости для Луны, если известна её масса и средний радиус.

Как мы уже упоминали, что практически осуществить запуск первого искусственного спутника Земли удалось 4 октября 1957 года, то есть спустя два с половиной столетия после открытия Ньютона. Сейчас же в околоземном пространстве движутся тысячи искусственных спутников Земли, запущенных учёными разных стран. Они обеспечивают непрерывный мониторинг погоды, различных природных явлений, трансляцию телевидения и так далее. А, например, спутниковая навигационная система ГЛОНАСС и другие системы глобального позиционирования позволяют определить координаты любой точки Земли с высокой степенью точностью.

Для полётов космических аппаратов к другим планетам и телам Солнечной системы необходимо производит очень точные расчёты траекторий с использованием законов небесной механики. При их запуске исходят из трёх основных соображений. Во-первых, геоцентрическая скорость космического аппарата при выходе на орбиту относительно Земли должна превышать вторую космическую скорость. Во-вторых, после преодоления притяжения Земли гелиоцентрическая орбита аппарата должна пересекаться с орбитой данной планеты (или другого небесного тела). А также необходимо подобрать такой момент запуска, чтобы орбита аппарата была наиболее оптимальной с точки зрения сроков полёта, затрат топлива и ряда других требований.

Одним из классов межпланетных траекторий являются энергетически оптимальные орбиты, которые соответствуют наименьшей геоцентрической скорости космических аппаратов в момент достижения границы сферы действия Земли.

Рассмотрим одну такую орбиту на примере Марса. Для простоты будем считать, что орбиты Марса и Земли являются круговыми. Для оптимального запуска нужно выбрать такой момент, когда орбитальная скорость Земли и скорость космического аппарата будут сонаправлены. При этом запускаемый аппарат и Марс, двигаясь по своим орбитам, должны одновременно достигнуть точки встречи.

Полученная нами орбита называется полуэллиптической или гомановской, в честь немецкого астронома Вальтера Гомана, занимавшегося теорией межпланетных полётов.

Теперь давайте рассчитаем время полёта Марса по этой полуэллиптической орбите, если его большая полуось равна 1,52 а. е.

Конструкция и оборудование современных космических аппаратов обеспечивают возможность совершения ими весьма сложных манёвров — выход на орбиту спутника планеты, посадка на планету и передвижение по её поверхности и т. п.