Методы классификации: преобразование пространства с помощью метода главных компонент. Дискриминантный анализ.

Метод главных компонент: Пусть имеется пространство, содержащее две выборки в факторном пространстве x₁ – x₂:

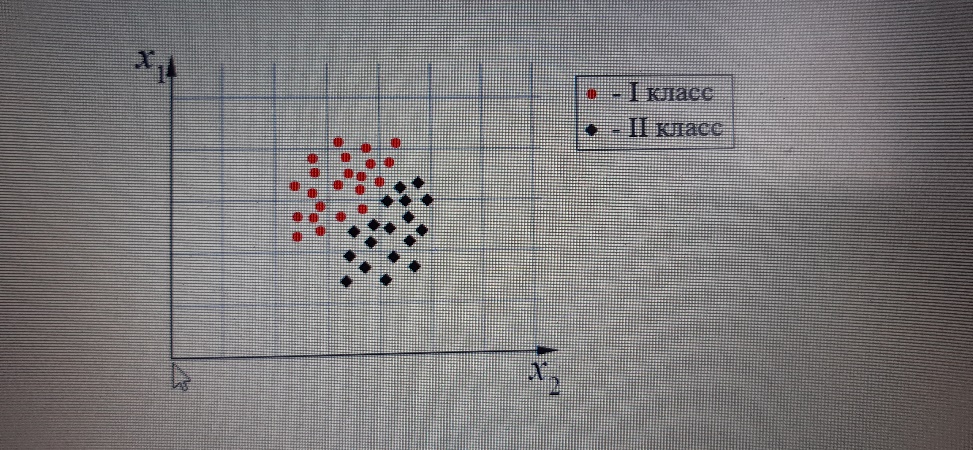
В имеющемся пространстве можно провести две прямые, разделяющие классы:

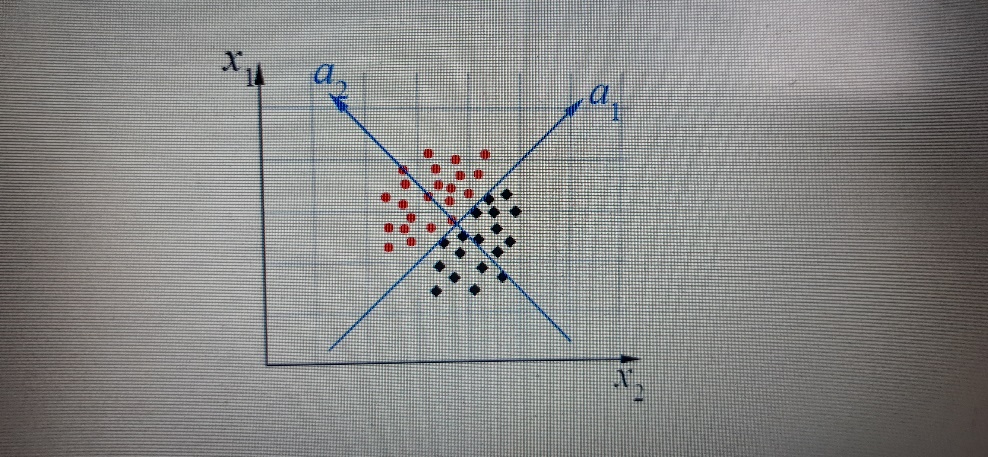
Вдоль оси a₂ классы разделены. Сама ось a₂ зависит от факторов x₁ и x₂. Таким образом, получили новую систему координат, которая является истинной двухмерной, где учтена зависимость факторов друг от друга.

Чтобы построить такую систему координат, сначала необходимо перенести точку начала отсчёта в центр выборки. Все точки выборки имеют координаты х₁ и х₂:

Далее вычисляют x_{1 ср.} и x_{2 ср.}. Тогда новый набор координат будет определяться следующим образом:

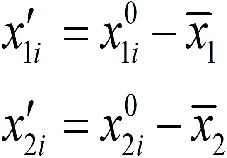
Осуществлен параллельный перенос:

Вычисляем дисперсии по обоим факторам:

Взаимозависимость факторов х₁ и х₂ определяем через вычисление ковариации:

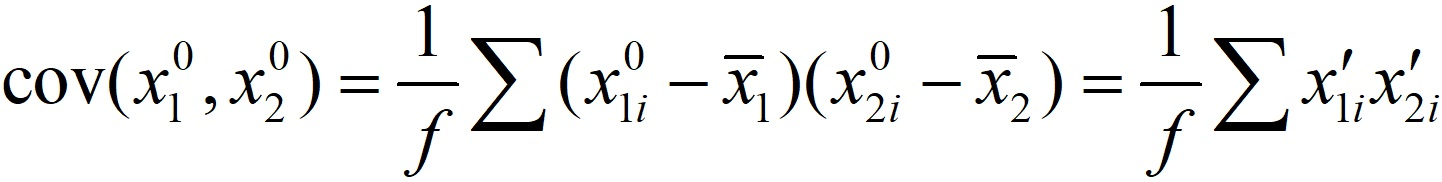
Строим матрицу ковариации:

Матрицу необходимо преобразовать – привести к диагональному виду. Для этого решают вековое уравнение:

covA = AΛ,

где А – матрица собственных векторов, Λ – матрица собственных значений.

Матрица Λ имеет вид:

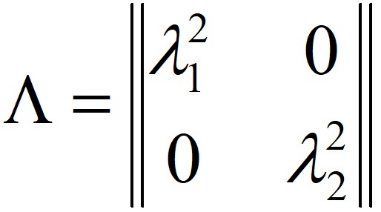
где λ²₁- дисперсия в новом пространстве.

Собственные векторы матрицы A являются осями нового пространства.

В новом пространстве уже можно вести анализ, и он будет оптимальным в данном пространстве по условию задачи. Новые оси а₁ и а₂ называют главными компонентами пространства. Соответственно, метод преобразования пространства получил название метода главных компонент.

Дискриминантный анализ: задача метода – среди множества факторов выбрать такой, по которому соединения были бы максимально близки друг к другу внутри класса, а классы максимально далеки друг от друга.

Математически это выражается следующим образом:

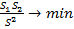(критерий Уилкса).

Чем это соотношение меньше, тем более достоверно разделяются классы в данном пространстве. Матрица Уилкса:

W =

Решив уравнение WA=AΛ, находят пространство с новыми осями, причём одна из них будет оптимально разделять выборку в данном пространстве.