Кинетическая энергия вращения
Механика твердого тела
Момент инерции
При изучении вращения твердого тела пользуются понятием момента инерции. Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс п материальных точек системы на квадраты их расстояний до рассматриваемой оси:
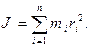
В случае непрерывного распределения масс эта сумма сводится к интегралу
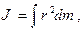
где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами х, у, z.
В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис. 24). Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним - r + dr. Момент инерции каждого полого цилиндра 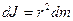 (так как dr<<r, то считаем, что расстояние всех точек цилиндра от оси равно г), где dm — масса всего элементарного цилиндpa. 2nrh dr — объем рассматриваемого элементарного цилиндра. Если ρ — плотность материала, то его масса
(так как dr<<r, то считаем, что расстояние всех точек цилиндра от оси равно г), где dm — масса всего элементарного цилиндpa. 2nrh dr — объем рассматриваемого элементарного цилиндра. Если ρ — плотность материала, то его масса 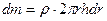 и dJ=2phrr3dr. Тогда момент инерции сплошного цилиндра
и dJ=2phrr3dr. Тогда момент инерции сплошного цилиндра
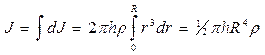
но так как pR4h — объем цилиндра, то его масса 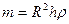 , а момент инерции
, а момент инерции
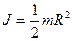
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы тела на квадрат расстояния а между осями: 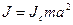 (16.1)
(16.1)
В заключение приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, m — масса тела).
Таблица1
| Тело | Положение оси вращения | Момент инерции |
| Полый тонкостенный цилиндр радиуса R | Ось симметрии | mR2 |
| Сплошной цилиндр или диск радиуса R | То же | 1/2 mR2 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | 1/3 ml2 |
| Шар радиуса R | Ось проходит через центр шара | 2/5 mR2 |
Кинетическая энергия вращения
Все реально существующие твердые тела под влиянием приложенных к ним сил деформируются, т. е. тем или иным образом изменяют свою форму. Для упрощения дальнейших рассуждений введем понятие абсолютно твердого тела. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками или, точнее, между двумя частицами, этого тела остается постоянным. В дальнейшем мы будем рассматривать только такого рода тела.
Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси OO, проходящей через него (рис. 25). Мысленно разобьем это тело на маленькие объемы с элементарными массами m1, т2 ... , mn, находящиеся на расстоянии r1, r2, ..., rn от оси вращения. При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами тn опишут окружности различных радиусов rn и будут иметь различные линейные скорости vn. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
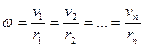 (17.1)
(17.1)
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
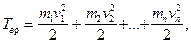
или 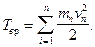
Используя выражение (17.1), получим
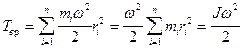
Таким образом, кинетическая энергия вращающегося тела
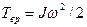 (17.2)
(17.2)
Из сравнения формулы (17.2) с выражением (12.1) для кинетической энергии тела, движущегося поступательно 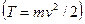 , следует, что момент инерции вращательного движения — мера инертности тела. Чем больше момент инерции, тем большую энергию нужно затратить для достижения данной скорости. Формула (17.2) справедлива для тела, вращающегося вокруг неподвижной оси.
, следует, что момент инерции вращательного движения — мера инертности тела. Чем больше момент инерции, тем большую энергию нужно затратить для достижения данной скорости. Формула (17.2) справедлива для тела, вращающегося вокруг неподвижной оси.
Для тела (колеса), катящегося по горизонтальной поверхности, энергия движения будет складываться из энергии поступательного движения и энергии вращения:
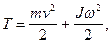
где m — масса катящегося тела, v — скорость поступательного движения, J — момент инерции тела, о) — скорость вращательного движения.
§ 18. Уравнение динамики вращательного
движения твердого тела
Если тело, закрепленное на оси, приводится во вращение какой-либо силой, то кинетическая энергия вращения возрастает на величину затраченной работы. Работа зависит от действующей силы и от произведенного ею перемещения, однако выражение работы для смещения материальной точки при вращательном движении неприменимо, так как в данном случае перемещение угловое.
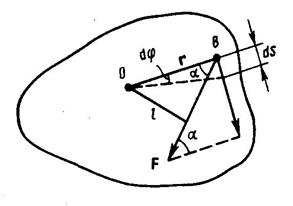 Найдем выражение для работы при вращении тела (рис. 26). Пусть сила F приложена в точке В, находящейся от оси вращения на расстоянии r, a — угол между направлением силы и радиусом-вектором. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на малый угол dj точка приложения В проходит путь
Найдем выражение для работы при вращении тела (рис. 26). Пусть сила F приложена в точке В, находящейся от оси вращения на расстоянии r, a — угол между направлением силы и радиусом-вектором. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на малый угол dj точка приложения В проходит путь 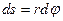 и работа равна произведению проекции силы на направление смещения на величину смещения:
и работа равна произведению проекции силы на направление смещения на величину смещения:
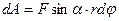 (18.1)
(18.1)
Величина
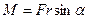 (18.2)
(18.2)
называется моментом силы относительно оси вращения; 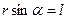 есть кратчайшее расстояние между линией действия силы и осью вращения, и называется плечом силы. Момент силы равен произведению силы на ее плечо:
есть кратчайшее расстояние между линией действия силы и осью вращения, и называется плечом силы. Момент силы равен произведению силы на ее плечо:
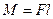
Момент силы — величина векторная. Так как 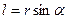 , то вектор
, то вектор
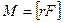
Его направление перпендикулярно плоскости, в которой расположен вектор силы, и он определяется по правилу правого винта.
Подставляя (18.2) в (18.1), получим, что работа при вращении тела равна произведению момента действующей силы на угол поворота:
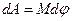
Работа при вращении тела идет на увеличение его кинетической энергии:
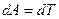 ,
,
но 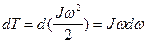
поэтому
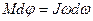
или
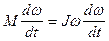
Учитывая, что w=dj/dt, получим
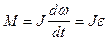 (18.3)
(18.3)
В векторной форме
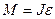 , (18.4)
, (18.4)
т. е. момент силы, действующей на тело, равен произведению момента инерции тела на угловое ускорение.
Уравнение (18.4) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
Дата добавления: 2017-06-13; просмотров: 6386;










