Базисные логические функции
Совокупность элементарных логических функций, с помощью которых можно записать любую функцию у, называется функционально полной системой функций или логическим базисом.
Три элементарные логические функций И, ИЛИ, НЕ составляют базис, который называется булевым базисом.
Функция логическое сложение (ИЛИ) переменных хn-1, хn-2,... х1, х0, записывается в виде
у=хn-1Úхn-2Ú...Úx0.
Значение у=0 имеет место только при x0 =x1=... =.хn-1=0. Если хотя бы одно слагаемое равно единице, то у = 1. Т. е. при любом числе слагаемых, равных единице, сумма их равна единице: у= 1, если x0=1,или x1=1,или xi=1,или все переменные х равны единице. Этим объясняется еще одно название рассматриваемой операции — операция ИЛИ.
Табл. 2 — таблица истинности операции ИЛИ двух переменных. В каждой ее строке записаны значения переменных x0 и x1 и соответствующее им значение функции у.
| Таблица 2 | ||
| X1 | X0 | УИЛИ |
Две двоичные переменные имеют четыре сочетания. В общем случае n двоичных переменных дают 2n сочетаний.
Устройство, выполняющее операцию дизъюнкции, называется дизъюнктором или элементом ИЛИ.
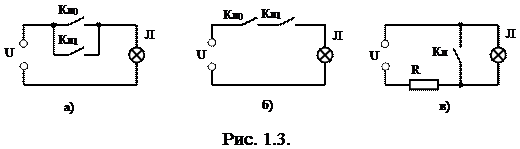
Электрическая реализация операции ИЛИ дана на рис. 3,а. Замкнутое состояние ключа соответствует логической единице (Кл=1), разомкнутое — логическому нулю (Кл=0). Лампочка будет светить (Л=1), если выполняются условия: ключ Кл0 замкнут, ключ Кл1 разомкнут – Кл0=1, Кл1=0 ИЛИ ключ Кл0 разомкнут, ключ Кл1 замкнут ИЛИ ключ Кл0 замкнут, ключ Кл1 замкнут.
Высказывание «лампочка светит, если...» может быть представлено функцией, реализующей операцию ИЛИ:
у=х0Úx1,
где X0 соответствует состоянию ключа Кл0, x1 — состоянию ключа Кл1, а у — состоянию лампочки.
Функция логическое умножение (И) n переменных записывается в виде
у=хn-1×хn-2×...×x0
Из приведенного выражения следует, что если хотя бы одна из переменных равна нулю, то функция равна нулю. Только в том случае, когда х0 = 1, И х1=1, И, ..., И хn-1= 1, y=1. Поэтому данная операция называется также операцией И.
| Таблица 3 | ||
| Х1 | X0 | УИ |
Табл.3 — таблица истинности операции И двух переменных.
Устройство, выполняющее операцию конъюнкция, называется конъюнктором или элементом И.
На рис. 3, б показана электрическая реализация операции И. Лампочка будет светить (у=1), если замкнуть ключ Кл0 (x0=1) и замкнуть ключ Кл1 (x1=1). Логическое уравнение, выражающее состояние лампочки, имеет вид
y=x0 x1,
где значения x0 и x1 соответствуют состояниям ключей Кл0 и Кл1.
Функция логическое отрицание (НЕ) записывается в виде у=`х.
| Таблица 4 | |
| X | УНЕ |
Табл. 4 — таблица истинности операции НЕ.
Устройство, выполняющее операцию инверсия, называется инвертором или элементом НЕ.
Электрическая реализация операции НЕ показана на рис. 3,в. Если ключ Кл замкнут (Кл= 1), то лампочка не светит (Л=0), при Кл=0 - Л=1.
Дата добавления: 2017-06-13; просмотров: 2789;











