Закон изменения сечения адиабатного потока
Условием неразрывности одномерного стационарного потока является одинаковость массового расхода G рабочего тела в любом сечении:
G=f·c/v=const, (6.14)
где f-площадь поперечного сечения канала.
Уравнение неразрывности потока (6.14) в дифференциальной форме имеет вид
 (6.15)
(6.15)
Совместное решение (6.15), (6.4) и уравнения адиабатного процесса pvk = const дает формулу связи изменения площади поперечного сечения (df) потока с изменением скорости (dc)
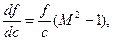 (6.16)
(6.16)
где М = c/a- число Маха.
 На основании (6.16) можно сделать следующие выводы:
На основании (6.16) можно сделать следующие выводы:
1. В дозвуковом адиабатном потоке выполняются следующие неравенства: с < а, М< 1, df/dc < 0, т.е. для увеличения скорости потока (dc > 0), его сечение должно уменьшаться (df< 0).
Суживающийся канал, называемый суживающимся соплом, предназначенный для увеличения скорости дозвуковых потоков, изображен на рис. 6.5. При достижении скорости потока, равной скорости звука, справедливы равенства: с = а, М= 1, df/dc = 0, df= 0, сужение канала должно прекратиться. Следовательно, невозможно получить сверхзвуковую скорость при истечении из суживающегося сопла.
При направлении дозвукового или звукового потока рабочего тела в расширяющийся канал, то скорость его будет уменьшаться, а давление увеличиваться. Такой канал называют диффузором, и он предназначен для сжатия рабочего тела в потоке.
2. В сверхзвуковом адиабатном потоке выполняются следующие неравенства: с>а, М>1, df/dc>0, т.е. для увеличения скорости потока (dc > 0)
его сечение должно возрастать (df > 0).
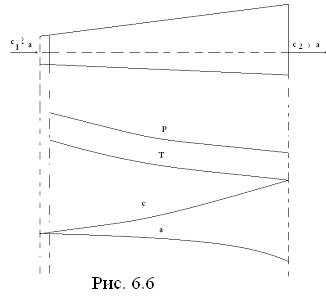
Расширяющиеся каналы, предназначенные для увеличения скорости звуковых и сверхзвуковых потоков, называются расширяющимися соплами (. 6.6).
3. Для непрерывного увеличения скорости потока от c1 < a (c1 = 0) до
c1 > а применяют комбинированные сопла, называемые соплами Лаваля (. 6.7).
Скорость в минимальном сечении сопла, равная скорости звука, называется критической скоростью (сkp = а). Параметры рабочего тела в минимальном сечении сопла также называются критическими (рkр, Тkp, vkp, hkp).
Если обозначить p2/p1 =β, а pkp/p1=βkp, то для суживающегося сопла всегда β≥βkp (p2≥pkp)для сопла Лаваля β<βkp(р2<ркр).

Расчет сопел
Целью расчета сопел является определение скорости истечения рабочего тела (с2), а также площади выходного (f2) и минимального (fmtn) (для сопел Лаваля) сечений.
Скорость истечения рабочего тела из сопла в соответствии с уравнением (6.2)
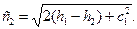 (6.17)
(6.17)
Для идеального газа в адиабатном процессе
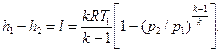
Тогда выражение (6 17) можно представить в виде
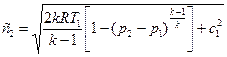 (6.18)
(6.18)
или с учетом р2/р1 =β,
 . (6.19)
. (6.19)
Площадь выходного сечения сопла рассчитывается по уравнению неразрывности потока
f2=Gv2/c2. (6.20)
Для минимального сечения сопла Лаваля можно получить аналогичные формулы:
 (6.21)
(6.21)
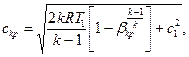 (6.22)
(6.22)
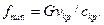 (6.23)
(6.23)
Как рассчитываются параметры: vкр, pкр, hкр в критическом сечении? Решение уравнений (6.22) при условии с1=0, а также 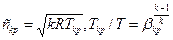 дает
дает
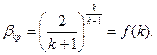 (6.24)
(6.24)
Численные значения βкр, полученные по формуле (6.24), приведены в табл. 6.1
Таблица 6.1
| Рабочее тело | k | βkp |
| Одноатомный газ | 1,67 | 0,484 |
| Двухатомный газ | 1,4 | 0,528 |
| Трех и многоатомный газ | 1,29 | 0,546 |
Давление в минимальном сечении сопла Лаваля рассчитывается по формуле
pkp=p1βkp (6.25)
Определение остальных критических параметров зависит от вида рабочего тела.
Для идеального газа
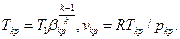
Для водяного пара критические параметры можно определить с помощью таблиц воды и водяного пара или по h-s- диаграмме в точке пересечения обратимого адиабатного процесса истечения/(s1== const) с изобарой pkp. Для перегретого пара можно принять βkр=0,546.
Выбор формы сопла
1. Для увеличения скорости звуковых и сверхзвуковых адиабатных по
токов (с1≥ а) применяют расширяющиеся сопла.
2. Для увеличения скорости дозвуковых потоков используют суживающиеся сопла или сопла Лаваля. Выбор формы сопла определяется давлением
среды (рс), куда происходит истечение. Для начальной скорости, равной нулю, с1 = 0:
а) при β=pc/p1 < βkp/p1 (pc <pkp, .6.7) следует применить
сопло Лаваля. В этом случае давление на выходе из сопла р2 = рс (расчетный
режим),с2>а;
б) при β= pc/p1≥βkp=pkp/p1, (pc≥pkp) следует использовать суживающееся сопло. В этом случае p2=рc (расчетный режим), с2≤а;
в) при  использовать суживающееся сопло, то давление на выходе из сопла будет критическим
использовать суживающееся сопло, то давление на выходе из сопла будет критическим 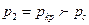 (нерасчетный режим), с2=а. На выходе суживающегося сопла невозможно получить давление газа ниже ркр, а скорость - выше скорости звука. Это приближенно справедливо и для истечения из не профилированного сопла, например из отверстия в сосуде, находящегося под давлением. Скорость истечения из таких отверстий не может превысить критическую, определяемую формулами (6.21), (6.22), а расход не может быть больше рассчитанного по формуле (6.23).
(нерасчетный режим), с2=а. На выходе суживающегося сопла невозможно получить давление газа ниже ркр, а скорость - выше скорости звука. Это приближенно справедливо и для истечения из не профилированного сопла, например из отверстия в сосуде, находящегося под давлением. Скорость истечения из таких отверстий не может превысить критическую, определяемую формулами (6.21), (6.22), а расход не может быть больше рассчитанного по формуле (6.23).
Если начальная скорость не равна нулю (0 < с1 < а), следует вычислить параметры торможения потока (р0, to, h0), имеющего скорость с1, и воспользоваться изложенной методикой выбора формы сопла для с1=0.
Дата добавления: 2021-07-22; просмотров: 564;











