Теплопередача герметичной и вентилируемой воздушных прослоек
Герметичные воздушные прослойки
Устройство воздушной прослойки является распространенным приемом теплозащиты. Прослойку используют в конструкциях окон, витражей, наружных стен и перекрытий, для экранирования при защите от излучения и как гравитационный побудитель для интенсификации конвективного теплосъема с обогревающих или охлаждающих устройств, а также для предупреждения переувлажнения конструкций.
Сопротивление теплопередаче воздушной прослойки Rв.п не может быть определено как сопротивление теплопроводности слоя воздуха, т.к. передача теплоты через воздушную прослойку от одной поверхности к другой происходит совместно теплопроводностью, конвекцией и излучением. Поток теплоты от одной стенки к другой можно представить в виде суммы конвективной qк и лучистой qл составляющих:
q = qк + qл (3.9)
Конвективный (включает передачу теплоты через воздух посредством теплопроводности) теплообмен qк в воздушной прослойке от одной поверхности к другой равен:
qк = a /к (t1 - t2), (3.10)
где a /к - коэффициент конвективного теплообмена, отнесенный к разности температур Dt = t1 - t2 на поверхностях прослойки.
Конвективный теплообмен в прослойке связан с циркуляцией воздуха. При ламинарном режиме течения (GrPr < 1000) критическая толщина прослойки dкр, мм, для которой сохраняется ламинарный режим течения:
dкр » 20 Dt1/3 (3.11)
При этом режиме в прослойке
a /к = lв/d, (3.12)
т.е. передача теплоты через слой воздуха толщиной d < dкр происходит теплопроводностью.
Если GrPr > 1000, то
a /к = 2,79 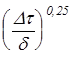 Вт/(м2 оС). (3.13)
Вт/(м2 оС). (3.13)
Лучистая составляющая теплопередачи через воздушную прослойку
qл = aл (t1 - t2), (3.14)
где aл - коэффициент лучистого теплообмена.
Коэффициент aл определяется по общей формуле aл = eпр со вj и при средней температуре 0оС, в = 0,81 aл = 3,95 Вт/(м2 оС).
Наиболее эффективная толщина прослойки для вертикальных слоев в ограждении равна 76...95 мм. Обычно в условиях ограждения утолщение прослойки более 50 мм не рационально, т.к. это незначительно уменьшает теплопередачу.
В конструкции покрытия здания воздушную прослойку можно расположить наклонно. Угол наклона при GrPr < 1000 не влияет на теплопередачу. При других режимах величину aк при заданном угле наклона можно определить линейной интерполяцией между его значениями при вертикальном и горизонтальном расположениях.
Нормативные данные сопротивления теплопередаче воздушных прослоек приведены в таблице 3.2.
Т а б л и ц а 3.2
Термические сопротивления герметичных воздушных прослоек
| Толщина | Rв.п, м2 оС/Вт | |||
| прослойки, мм | для горизонтальных прослоек при потоке теплоты снизу-вверх и для вертикальных прослоек | для горизонтальных прослоек при потоке теплоты сверху вниз | ||
| летом | зимой | летом | зимой | |
| 0,17 | 0,20 | 0,17 | 0,21 | |
| 0,18 | 0,21 | 0,21 | 0,26 | |
| 0,18 | 0,22 | 0,22 | 0,28 | |
| 0,18 | 0,23 | 0,23 | 0,30 | |
| 0,20 | 0,24 | 0,24 | 0,31 | |
| 0,21 | 0,24 | 0,26 | 0,33 | |
| 200...300 | 0,21 | 0,26 | 0,26 | 0,33 |
Вентилируемые воздушные прослойки
Рассмотрим стационарный тепловой режим ограждения с воздушной прослойкой, через которую непрерывно продувается воздух (рис. 3.5). Вентилируемая прослойка отделена от помещения с температурой tв внутренней частью конструкции, имеющей коэффициент теплопередачи kв.
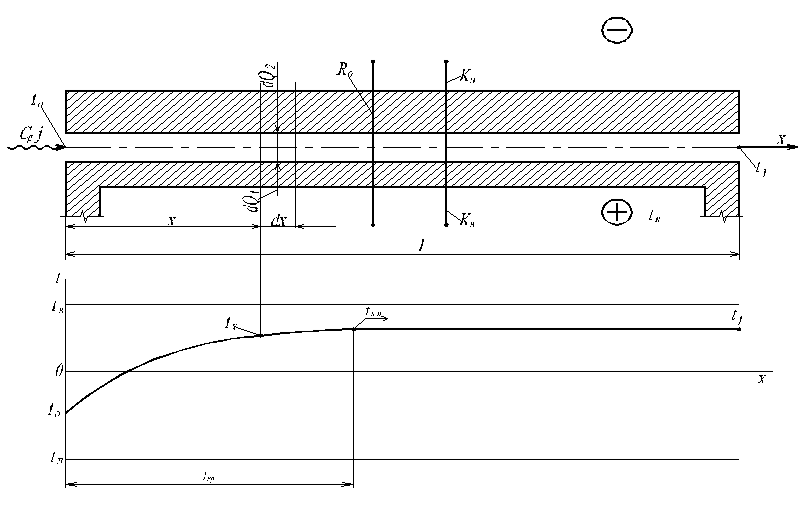
Рис. 3.5. К выводу уравнения теплопередачи через ограждение с вентилируемой воздушной прослойкой
Наружная часть конструкции имеет коэффициент теплопередачи kн и отделяет продух от наружного воздуха с температурой tн. Воздух в прослойку поступает с температурой tо (в общем случае отличной от tн и tв) и, проходя через нее, изменяет свою температуру. На некотором расстоянии 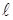 кр поток воздуха приобретает некоторую неизменную температуру tв.п, зависящую только от условий передачи теплоты через ограждение и не связанную с его начальной температурой.
кр поток воздуха приобретает некоторую неизменную температуру tв.п, зависящую только от условий передачи теплоты через ограждение и не связанную с его начальной температурой.
Задача состоит в определении температуры воздуха t в произвольном сечении прослойки и в определении теплопередачи через такую конструкцию. Определим температуру tв.п по формуле (3.3):
tв.п = tв - 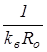 (tв - tн) =
(tв - tн) = 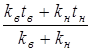 (3.15)
(3.15)
qв.п = 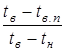 =
= 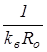 =
= 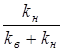 , (3.16)
, (3.16)
где Rо = 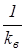 +
+ 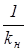 =
= 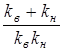
Значения kв и kн равны
kв = 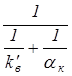 ; kн =
; kн = 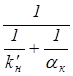 , (3.17)
, (3.17)
где 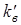 и
и 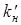 - коэффициенты теплопередачи внутренней и наружной части ограждения от поверхностей воздушной прослойки;
- коэффициенты теплопередачи внутренней и наружной части ограждения от поверхностей воздушной прослойки;
aк - коэффициент конвективного теплообмена одной поверхности с воздухом, движущимся в прослойке со скоростью u, м/с.
Среднее значение aк, Вт/(м2 оС), для воздуха по длине прослойки при ламинарном режиме движения (Re < 2×103) в канале
aк = 1,163 (0,77 + 1,3×10-3t) 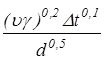 e, (3.18)
e, (3.18)
Dt - разность температур воздуха и поверхности воздушной прослойки;
d - эквивалентный диаметр, равный 4F/Р (F - площадь и Р - периметр канала), для прослойки (щелевой канал) d = 2d.
Коэффициент e в формуле (3.18) отличается от 1,0 для каналов, длина которых 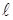 меньше 50d.
меньше 50d.
При турбулентном режиме течения (Re > 2×103)
aк = 1,163 (2,7 + 1,5×10-3t) 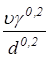 e (3.19)
e (3.19)
При малых расходах воздуха температура tв.п устанавливается на близком расстоянии от входа в прослойку и остается неизменной по всей длине прослойки. При определении сопротивления теплопередаче ограждения Rо величину Rв.п необходимо принимать
Rв.п = 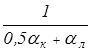 , (3.20)
, (3.20)
где aк - определяется по (3.18) или (3.19);
aл - определяется как и в формуле (3.14).
Расход воздуха j (рис. 3.6) в вентилируемой прослойке определяется гидравлическим расчетом, заключающимся в определении разности давлений Dр, под влиянием которой происходит движение воздуха, и в получении расчетного расхода, при котором гидравлические потери в прослойке DН равны перепаду давлений Dр.
Давление Dр равно сумме ветрового (Dрu) и гравитационного (Dрt) давлений:
Dр = Dрu + Dрt (3.21)
Величина Dрu равна
Dрu = (k1- k2) 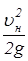 g » (k1- k2)
g » (k1- k2) 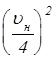 , (3.22)
, (3.22)
где k1 и k2 - аэродинамические коэффициенты на входе в прослойку и на выходе из нее.
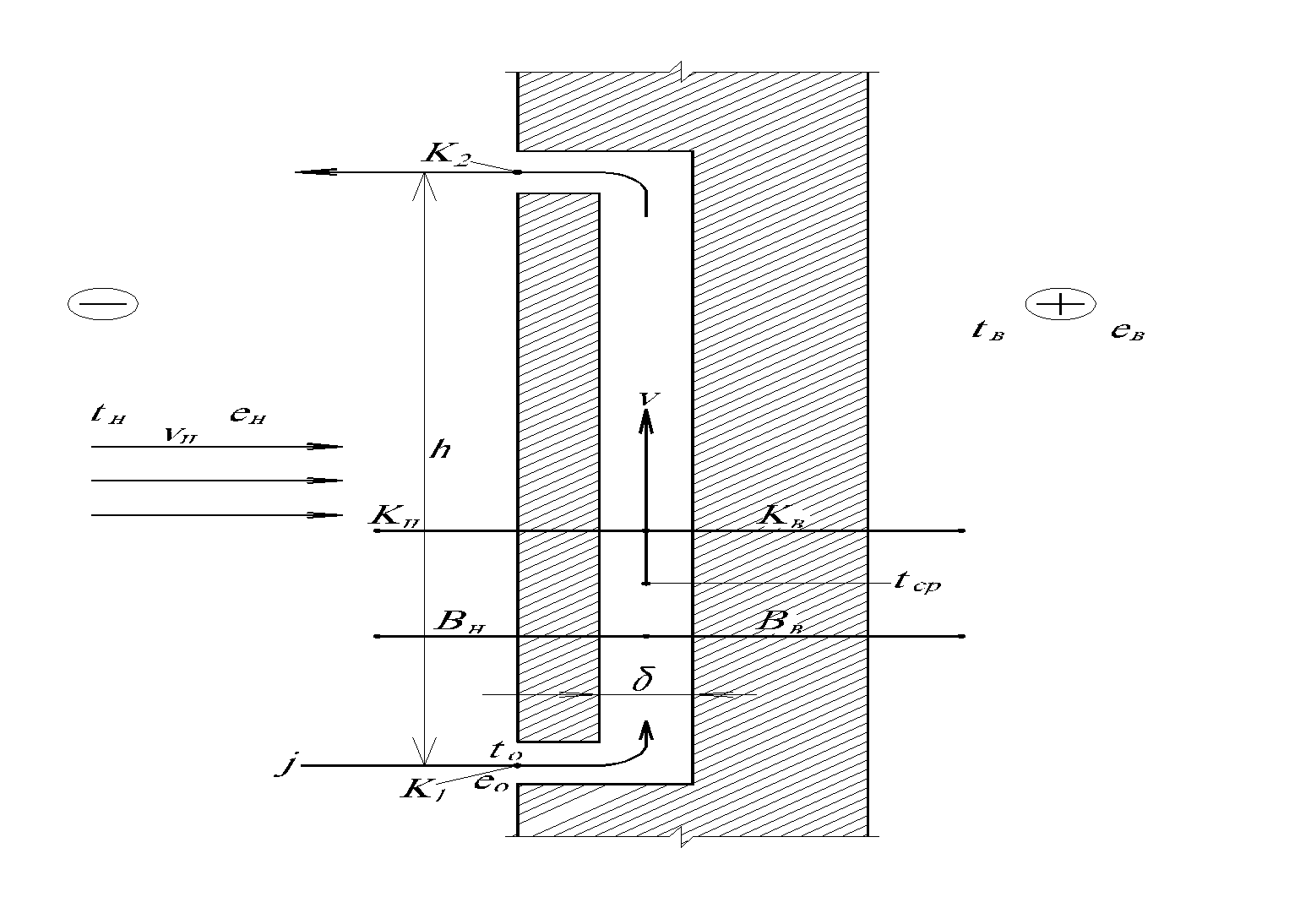
Рис. 3.6. Теплопередача через ограждение с прослойкой, вентилируемой за счет гравитационных сил и ветра
Гравитационное давление Dрt возникает за счет разности объемных весов в прослойке gср и наружного воздуха gн:
Dрt = (gн - gср)h » 5×10-3 (tср - tн)h, (3.23)
где h - разность высот отверстий входа воздуха в прослойку и выхода из нее.
Потери давления в прослойке определяются только местными сопротивлениями x:
DН = Sx 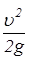 g » Sx
g » Sx 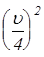 , (3.24)
, (3.24)
где x = 0,5 на входе, x = 1,0 на выходе, x = 1,0 на каждый поворот воздуха.
Расход воздуха равен:
j = u g d ×3600, (3.25)
где d - толщина воздушной прослойки, м.
Из условия равенства располагаемого давления (3.21) и гидравлических потерь (3.24) при Sx = 0,5 + 1,0 + 2×1,0 = 3,5 и k1 » k2 и после некоторых упрощений определим приближенную формулу для определения скорости воздуха в прослойке:
u = 0,15 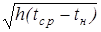 (3.26)
(3.26)
Изложенный метод позволяет провести совместный расчет взаимосвязанных теплового и гидравлического режимов вентилируемой прослойки.
Дата добавления: 2021-07-22; просмотров: 1031;











