Суммирующий счетчик

Суммирующий асинхронный счетчик с последовательным переносом

В суммирующих счетчиках записанное число при каждом входном импульсе, увеличивается на 1. Поэтому их строят с учетом правила увеличения двоичного кода на 1: «Двоичный код числа А+1 получается из двоичного кода числа А путем инвертирования младшего из нулей и старших правее него единиц».

Например,

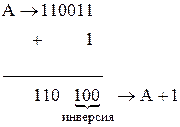
Из этого правила можно сделать следующие выводы:

- триггер младшего (нулевого) разряда должен переключаться при воздействии каждого единичного сигнала;

- при очередном входном единичном сигнале 1-й триггер счетчика переключается независимо от исходного состояния, если все триггеры предыдущих младших разрядов переключаются из состояния Q=1 в состояние Q=0;

- переключение i-го триггера вызывается отрицательным перепадом на входе 1/0.

На основании этих выводов заключаем, что при построении суммирующего счетчика на асинхронных Т-триггерах инверсные Т-входы триггеров следует соединять с прямыми выходами предыдущих триггеров, а при прямых Т-входах их надо соединять с инверсными выходами предыдущих триггеров. Рассмотрим трехразрядный суммирующий счетчик на асинхронных Т-триггерах с инверсными Т-входами (см. рис. 5.8.).

Рис. 5.8.

В начале работы все триггеры счетчика установлены в нулевое состояние. Затем в каждом такте на счетный вход младшего триггера ТТ₀ поступает очередной импульс (n+1), окончание которого вызывает переход в единичное состояние только триггера ТТ₀. Его вход является счетным входом следующего триггера ТТ₁ и т.д. Из временных диаграмм и соответствующих двоичных обозначений состояний триггеров следует, что в промежутках между входными сигналами состояние счетчика представляет собой двоичный код числа поступивших сигналов.

Когда все n триггеров заполнены единицами, то в счетчике записано наибольшее число 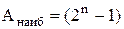. Очередной 2ⁿ-й импульс обнуляет счетчик, и далее ведется новый цикл счета от 0 до 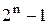. Каждый триггер счетчика является делителем частоты поступивших на его вход импульсов на два. Общий коэффициент деления счетчика равен К_С=2.

Запуск каждого последующего триггера счетчика происходит только после срабатывания предыдущего, т.е. с некоторой задержкой (рис. 5.8). Это снижает быстродействие счетчика: его разрешающее время будет возрастать пропорционально количеству разрядов 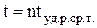, где t_{уд.р.ср.т.}- среднее время задержки распространения сигнала при срабатывании одного триггера. Отсюда с учетом длительности входного импульса in максимальная частота работы счетчика с последовательным переносом и соответственно минимальный период повторения входных импульсов определяются по формулам:

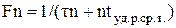; Т_н=1/Fn.

Помимо суммирующих, существуют вычитающие и реверсивные счетчики с последовательностным переносом. Принцип их построения аналогичен вышеописанному, т.е. перенос (переключение триггеров) осуществляется последовательно (последующий триггер переключается только после переключения предыдущего).

Вычитающий счетчик

Вычитающий счетчик с последовательным переносом. Чтобы выяснить принцип построения вычитающего счетчика, вычтем из двоичного числа единицу:

_111001 111000

1 1

111000 110111

Если в каждом примере поразрядно сравнить исходное число и результат (111001 и 111000, а также 111000 и 110111), то можно сделать вывод, что младший разряд исходного числа переключается всегда; каждый более старший разряд переключается, если предыдущий переключился из 0 в 1.

Применительно к рассматриваемому счетчику на вычитание это означает, что счетные импульсы следует подавать на вход триггера младшего разряда, а между собой триггеры должны быть соединены так, чтобы обеспечить переключение последующего, когда предыдущий по прямому выходу переходит из 0 в 1. Для выполнения последнего условия счетный вход последующего триггера следует соединить с инверсным выходом предыдущего, если триггеры переключаются перепадом 1/0, или с прямым выходом, если триггеры переключаются перепадом 0/1.

Схема вычитающего счетчика на триггерах, переключающихся перепадом 1/0, приведена на рис. По входам S в разряды счетчика заносится двоичное число, из которого нужно вычесть число, представляемое количеством входных импульсов.

Пусть, например, в счетчик (рис.) записано число 5₁₀=101₂. Первым входным импульсом триггер Т1 переключится из 1 в 0 (по прямому выходу); при этом на инверсном выходе возникает перепад 0/1, которым триггер Т2переключиться не сможет; в счетчике останется число 100₂ = 4₁₀. Второй входной импульс устанавливает Т1 в состояние 1, на выходе появляется перепад 1/0, который переключает Т2в состояние 1, а формирующийся при этом на Q₂перепад 1/0 переключает ТЗ в состояние 0 – в счетчике остается число 011₂ = 3₁₀. Аналогично можно рассмотреть действие последующих входных импульсов. Очевидно, что после пятого входного импульса во все разряды счетчика будут записаны нули.

Нетрудно установить, что следующий импульс, воздействуя на обнуленный счетчик, переключит все его триггеры в 1.

Счетчики с последовательным переносом, имея простую структуру, обладают рядом недостатков. Один из них состоит в сравнительно низком быстродействии: к к-му разряду переключающий сигнал проходит через к– 1 предыдущих, поэтому интервал между соседними входными импульсами должен превышать t_n (п – 1), где t_п – время переключения триггера; п – число разрядов счетчика. Другим недостатком является то, что в ходе переключения младшие разряды счетчика принимают уже новые состояния, в то время как старшие еще находятся в прежнем, т. е. при смене одного числа другим счетчик проходит ряд промежуточных состояний, каждое из которых может быть принято за двоичный код числа прошедших на входе импульсов.

Когда для устройства, куда входит счетчик, отмеченные недостатки являются существенными, используют счетчик с параллельным переносом.