Динамика вращательного движения твердого тела. Закон сохранения момента импульса
Для описания вращения тела вокруг неподвижной оси используются следующие физические величины:
1. Момент инерции тела I относительно заданной оси, характеризующий инертность тела в отношении вращательного движения.
2. Момент импульса тела L=Iw относительно заданной оси, являющийся количественной мерой вращательного движения тела, ω– угловая скорость вращения тела вокруг оси.
3. Момент силы М относительно заданной оси, который действует на тело и определяет скорость изменения во времени его момента импульса относительно оси вращения
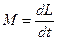 . .
| (3.0.1) |
Если при вращении момент инерции тела остается постоянным, то уравнение вращательного движения преобразуется к виду:
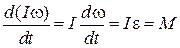 , ,
| (3.0.2) |
где 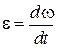 – угловое ускорение тела.
– угловое ускорение тела.
При описании вращательного движения твердого тела вокруг неподвижной точки используется момент импульса относительно точки, который определяется с помощью векторного произведения
 , ,
| (3.0.3) |
где 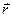 – радиус-вектор, проведенный из выбранной точки в ту точку, где находится начало вектора импульса
– радиус-вектор, проведенный из выбранной точки в ту точку, где находится начало вектора импульса 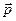 (в точку нахождения частицы).
(в точку нахождения частицы).
Аналогично можно определить вектор момента 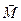 силы
силы 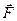 относительно заданной точки
относительно заданной точки
 . .
| (3.0.4) |
Момент импульса 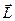 или силы
или силы 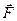 относительно точки О обозначается как
относительно точки О обозначается как  или
или  (рис. 3.01).
(рис. 3.01).
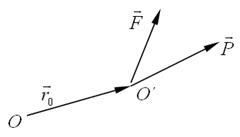
Рис. 3.01
Точка О – начало координат, 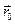 – радиус-вектор точки O´, где находится начало вектора
– радиус-вектор точки O´, где находится начало вектора 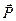 и точка приложения силы
и точка приложения силы 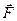 .
.
Рассмотрим проекцию вектора  на ось z, проходящую через точку О. Из выражения (3.0.4) получим:
на ось z, проходящую через точку О. Из выражения (3.0.4) получим:
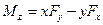 . .
| (3.0.5) |
Величина Mz называется моментом силы 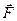 относительно заданной оси z. Важно отметить, что Mz не зависит от координаты z точки приложения силы и определяется только той компонентой силы, которая лежит в плоскости, перпендикулярной оси z. Эта компонента обозначается
относительно заданной оси z. Важно отметить, что Mz не зависит от координаты z точки приложения силы и определяется только той компонентой силы, которая лежит в плоскости, перпендикулярной оси z. Эта компонента обозначается 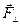 . Соответственно,
. Соответственно, 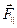 обозначает компоненту силы, параллельную оси z (рис. 3.02). Таким образом, полная сила
обозначает компоненту силы, параллельную оси z (рис. 3.02). Таким образом, полная сила
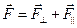 . .
| (3.0.6) |
Момент силы 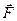 относительно оси z можно записать следующим образом:
относительно оси z можно записать следующим образом:
 . .
| (3.0.7) |
Длина отрезка 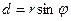 , перпендикулярного к его компоненте силы
, перпендикулярного к его компоненте силы 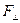 , называется плечом силы
, называется плечом силы 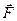 , j – угол между радиусом-вектором
, j – угол между радиусом-вектором 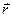 и компонентой силы
и компонентой силы 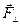 . Отрезки прямых d, r и
. Отрезки прямых d, r и 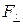 лежат в плоскости проходящей через точку O´ приложении силы
лежат в плоскости проходящей через точку O´ приложении силы 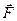 перпендикулярно оси z. Выбор знака в формуле (3.0.7) зависит от ориентации вектора
перпендикулярно оси z. Выбор знака в формуле (3.0.7) зависит от ориентации вектора 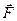 относительно оси z.
относительно оси z.
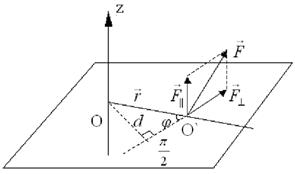
Рис. 3.02
Точка О – точка пересечения плоскости, проходящей через точку O´ приложения силы 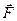 перпендикулярно оси z.
перпендикулярно оси z.
Для описания вращения твердого тела вокруг неподвижной оси используется уравнение моментов относительно этой оси
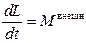 , ,
| (3.0.8) |
где
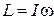
| (3.0.9) |
- момент импульса твердого тела относительно оси вращения, I – момент инерции твердого тела относительно этой оси, ω - угловая скорость вращения твердого тела и  - момент всех внешних сил, действующих на тело, относительно рассматриваемой оси. Согласно третьему закону Ньютона, суммарный момент всех внутренних сил относительно произвольной оси всегда равен нулю.
- момент всех внешних сил, действующих на тело, относительно рассматриваемой оси. Согласно третьему закону Ньютона, суммарный момент всех внутренних сил относительно произвольной оси всегда равен нулю.
Если при вращении твердого тела его момент инерции сохраняется постоянным, уравнение моментов относительно неподвижной оси упрощается и принимает вид:
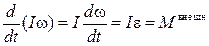 , ,
| (3.0.10) |
где
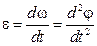
| (3.0.10) |
-угловое ускорение твердого тела и φ - угол поворота твердого тела вокруг оси вращения.
Из уравнения моментов относительно неподвижной оси следует, что момент импульса относительно этой оси сохраняется постоянным
 , ,
| (3.0.11) |
если полный момент всех внешних сил, действующих на твердое тело, относительно рассматриваемой оси равен нулю
| Мвнешн =0 . | (3.0.12) |
Кинетическая энергия K твердого тела, вращающегося вокруг неподвижной оси, описывается выражением
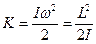 . .
| (3.0.13) |
Изменение кинетической энергии K может быть обусловлено работой как внешних, так и внутренних сил, поэтому
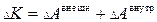 . .
| (3.0.14) |
При повороте абсолютно твердого тела на бесконечно малый угол Δφ работа внешних сил
| ΔАвнешн= МвнешнΔφ. | (3.0.15) |
Если полный момент внешних сил, действующих на тело равен нулю, то изменение кинетической энергии вращающегося тела возможно за счет работы внутренних сил, которая меняет момент инерции твердого тела
 . .
| (3.0.16) |
Здесь L = const, поскольку Мвнешн= 0.
Задача №7
В устройстве, показанном на рис.7.1, определите ускорения тел с массами m1 и m2 (m1 > m2), связанных невесомой, нерастяжимой нитью, перекинутой через блок. Блок представляет собой однородный цилиндр с массой М и радиусом R. Нить по блоку не проскальзывает, трение в оси блока пренебрежимо мало. Ускорение свободного падения g.
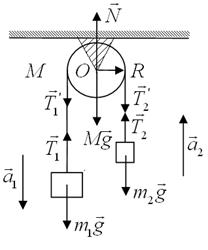
Рис.7.1
Решение
1. Определим все силы, действующие на тела системы с отличной от нуля массой: силы тяжести 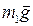 ,
, 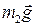 ,
, 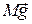 , силы натяжения нити
, силы натяжения нити 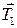 ,
,  ,
, 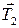 ,
, 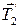 и сила реакции
и сила реакции 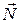 крепления блока.
крепления блока.
2. Запишем в векторной форме уравнения поступательного движения тел 1 и 2
 , ,
| (3.7.1) |
 . .
| (3.7.2) |
Для блока поступательное движение отсутствует, поэтому
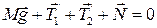 . .
| (3.7.3) |
Блок совершает вращательное движение вокруг своей оси симметрии, проходящей через центр масс блока перпендикулярно плоскости рисунка. Уравнение моментов относительно оси вращения блока имеет вид
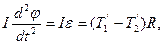
| (3.7.4) |
где момент инерции однородного блока относительно его оси симметрии
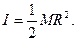
| (3.7.5) |
3. Перейдем от векторной формы записи уравнений (3.7.1) - (3.7.2) к скалярной, используя проекции этих уравнений на направления ускорений тел 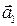 и
и 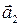
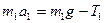 , ,
| (3.7.6) |
 , ,
| (3.7.7) |
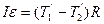 , ,
| (3.7.8) |
которая содержит 7 неизвестных величин: 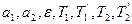 .
.
4. Получим полную систему из 7 независимых уравнений, используя законы физики и условия задачи.
Благодаря нерастяжимости нити величины ускорений тел одинаковые:
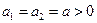 . .
| (3.7.9) |
Поскольку нить не проскальзывает по поверхности блока, то в каждой точке контакта линейные скорости элементов нити υ и поверхности блока ωR равны по величине
| υ=ωR. | (3.7.10) |
Отсюда получаем, что величины ускорения a тел и углового ускорения ε блока связаны соотношением
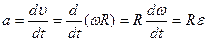 . .
| (3.7.11) |
Согласно условию задачи нить невесомая, поэтому сила натяжения одинаковая во всех точках нити слева от блока
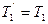 , ,
| (3.7.12) |
и во всех точках нити справа от блока
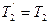 . .
| (3.7.13) |
На основе уравнений (3.7.6) – (3.7.13) приходим к полной системе из 4 независимых уравнений для нахождения 4 неизвестных величин:
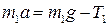 , ,
| (3.7.14) |
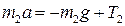 , ,
| (3.7.15) |
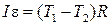 , ,
| (3.7.16) |
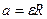 . .
| (3.7.17) |
5. Решая систему уравнений (3.7.14) – (3.7.17), находим величину ускорения тел
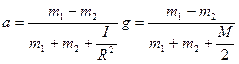 . .
| (3.7.18) |
Согласно полученному результату учет массы блока уменьшает ускорение тел.
Ответ: 
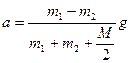 .
.
Задача №8
Маховик в виде однородного диска с массой m=10кг и радиусом R=0,2м вращается вокруг своей оси симметрии с начальной угловой скоростью ω0=100рад/с. В момент времени t=0 к маховику начинают прижимать две тормозные колодки с силой F=50H каждая (рис.17.1). Коэффициент трения скольжения между маховиком и тормозными колодками μ=0,3. Определите изменение во времени угловой скорости ω(t) вращения маховика. Через какое время t1 маховик остановиться?
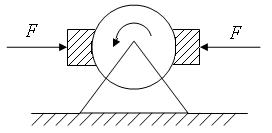
Рис.8.1
Решение
Уравнение моментов относительно оси вращения маховика имеет вид
 , ,
| (3.8.1) |
где μF – сила трения скольжения между маховиком и тормозной колодкой и
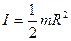
| (3.8.2) |
-момент инерции маховика относительно его оси симметрии.
Разделим переменные ω и t в дифференциальном уравнении (3.8.1)
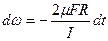
| (3.8.3) |
и проинтегрируем левую часть полученного равенства по ω от начальной угловой скорости ωо до текущей угловой скорости ω(t), а правую часть по t от начального момента времени t=0до текущего момента t
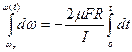
| (3.8.4) |
Выполняя интегрирование, получим зависимость угловой скорости маховика от времени
 . .
| (3.8.5) |
Время t1, через которое маховик остановится, находится с помощью уравнения
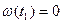 . .
| (3.8.6) |
Отсюда следует, что время остановки маховика
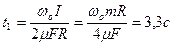 . .
| (3.8.7) |
Ответ:  ,
, 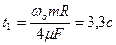 .
.
Задача №9
Однородный цилиндр массой с m и радиусом R скатывается без проскальзывания по наклонной плоскости с углом наклона α относительно горизонтали (рис.9.1). Ускорение свободного падения g. Определите ускорение 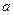 центра масс цилиндра. Как со временем изменяется скорость υ центра масс цилиндра, если его начальная скорость равнялась нулю?
центра масс цилиндра. Как со временем изменяется скорость υ центра масс цилиндра, если его начальная скорость равнялась нулю?
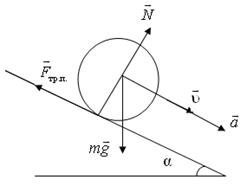
Рис.9.1
Решение
1.Определим все силы, которые действуют на цилиндр согласно условиям задачи: сила тяжести  , сила реакции опоры
, сила реакции опоры 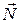 и сила трения покоя
и сила трения покоя 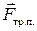 , поскольку цилиндр скатывается без проскальзывания.
, поскольку цилиндр скатывается без проскальзывания.
2. Запишем уравнение движения центра масс цилиндра в векторной форме
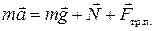 . .
| (3.9.1) |
Кроме поступательного движения цилиндр совершает вращение вокруг своей оси симметрии с угловой скоростью ω, которая меняется со временем. Соответствующий вращающий момент создает только сила трения покоя, поскольку векторы силы тяжести и силы реакции опоры проходят через ось вращения и поэтому их вращающие моменты равны нулю.
Поскольку ось вращения перемещается в пространстве таким образом, что все время остается параллельной самой себе в разные моменты времени, то уравнение моментов записывается точно так же, как для неподвижной оси:
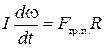 , ,
| (3.9.2) |
где
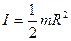
| (3.9.3) |
- момент инерции однородного цилиндра относительно его оси симметрии.
3. Перейдем от векторной формы записи уравнения (3.9.1) к скалярной, используя проекции на направление вектора ускорения  ,
,
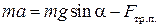 . .
| (3.9.4) |
При этом выполняется равенство
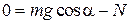 , ,
| (3.9.5) |
поскольку центр масс цилиндра не имеет ускорения в направлении, перпендикулярном к наклонной плоскости.
Уравнения поступательного (3.9.4), (3.9.5) и вращательного (3.9.2) движений цилиндра содержат 4 неизвестных величины: a, N, 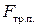 и
и 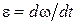 . Следовательно, на основе условий задачи и законов физики необходимо найти четвертое уравнение, связывающее неизвестные величины.
. Следовательно, на основе условий задачи и законов физики необходимо найти четвертое уравнение, связывающее неизвестные величины.
4. Согласно условиям задачи цилиндр скатывается без проскальзывания, поэтому в области касания поверхности цилиндра с наклонной плоскостью скорость элементов поверхности цилиндра равна нулю и поэтому справедливо соотношение
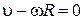 , ,
| (3.9.6) |
где υ - скорость поступательного движения цилиндра, равная скорости движения центра масс, и ωR - линейная скорость элементов поверхности цилиндра, связанная с его вращением вокруг оси симметрии.
Дифференцируя уравнение (3.9.6) по времени, получим связь между величинами линейного ускорения a и углового ускорения цилиндра ε
| a-εR=0 . | (3.9.7) |
Таким образом, полная система уравнений для 4 неизвестных величин имеет вид:
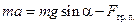
| (3.9.8) |
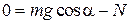 , ,
| (3.9.9) |
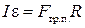 , ,
| (3.9.10) |
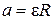 . .
| (3.9.11) |
5. Решая систему уравнений (3.9.8) – (3.9.11), получим
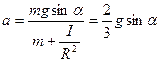 . .
| (3.9.12) |
Сила трения покоя не должна превышать силу трения скольжения, поэтому должно выполняться условие
 , ,
| (3.9.13) |
или
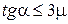 . .
| (3.9.14) |
Только при выполнении условия (3.9.14) возможно скатывание цилиндра без проскальзывания.
Ответ: 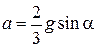 ,
, 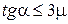 , μ– коэффициент трения скольжения между цилиндром и наклонной плоскостью.
, μ– коэффициент трения скольжения между цилиндром и наклонной плоскостью.
Дата добавления: 2021-07-22; просмотров: 533;











