ПРИ НАГРУЗКЕ. ВЕКТОРНЫЕ ДИАГРАММЫ
Для определения МДС обмотки возбуждения при нагрузке используют векторные диаграммы (рис. 10-27).
Для их построения целесообразно использовать относительные значения параметров тока, напряжения, ЭДС и МДС.
Для более точного определения потока рассеяния полюсов при нагрузке необходимо иметь частичные характеристики намагничивания:
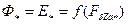 ,
, 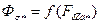 ,
, 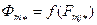 .
.
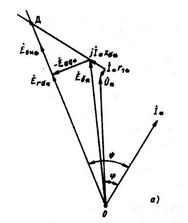
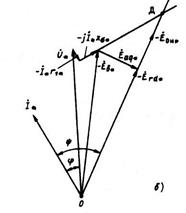
Рис. 10.27. векторные диаграммы:
а — для генератора; б — для двигателя
Здесь принято 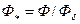 ,
, 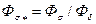 ,
, 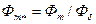 ;
; 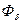 — базовое значение потока, равное потоку при номинальном фазном напряжении;
— базовое значение потока, равное потоку при номинальном фазном напряжении;
 ;
;
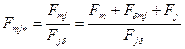 ;
;
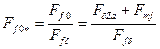 ;
;
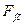 —базовое значение МДС, равное МДС обмотки возбуждения при холостом ходе и номинальном фазном напряжении. На рис. 10.28 все характеристики имеют одинаковые масштабы по соответствующим осям координат.
—базовое значение МДС, равное МДС обмотки возбуждения при холостом ходе и номинальном фазном напряжении. На рис. 10.28 все характеристики имеют одинаковые масштабы по соответствующим осям координат.

Рис. 10.28. Частичные характеристики намагничивания
Для оценки насыщения машины удобно построить зависимость 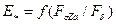 (рис. 10.29). Указанные графики строятся по данным расчета магнитной цепи машины.
(рис. 10.29). Указанные графики строятся по данным расчета магнитной цепи машины.
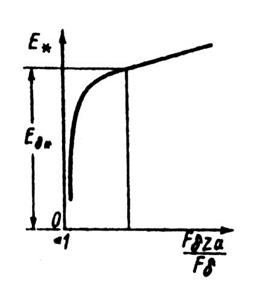
Рис. 10.29. Зависимость 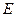 от отношения
от отношения 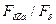
Диаграмма при заданных номинальных значениях тока 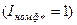 , напряжения
, напряжения 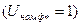 и угла между ними строится следующим образом.
и угла между ними строится следующим образом.
1. В выбранном масштабе для тока и напряжения откладывают вектор номинального фазного тока и под углом 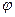 к нему— вектор фазного напряжения.
к нему— вектор фазного напряжения.
2. К вектору напряжения пристраивают векторы падения напряжения 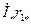 ,
, 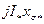 , для генератора и
, для генератора и 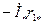 ,
, 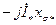 , для двигателя, в результате чего находят ЭДС
, для двигателя, в результате чего находят ЭДС 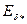 , которая индуктируется в обмотке якоря при нагрузке. При
, которая индуктируется в обмотке якоря при нагрузке. При 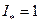 векторы падения напряжения численно равны
векторы падения напряжения численно равны 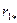 и
и 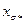 . В крупных машинах падение напряжения в активном сопротивлении
. В крупных машинах падение напряжения в активном сопротивлении 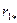 относительно мало и им можно пренебречь.
относительно мало и им можно пренебречь.
3. По 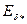 из зависимости
из зависимости 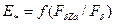 определяют отношение
определяют отношение 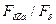 , по которому из рис. 10.25 находят коэффициенты
, по которому из рис. 10.25 находят коэффициенты 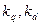 и
и 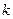 .
.
4. Определяют значение результирующей ЭДС по продольной оси 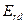 и угол
и угол 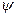 . Для этой цели находят МДС (в относительных единицах):
. Для этой цели находят МДС (в относительных единицах):
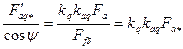 ,
,
где
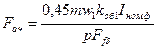 .
.
Отложив 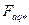 по оси абсцисс характеристики
по оси абсцисс характеристики 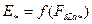 , на оси ординат получают ЭДС, равную
, на оси ординат получают ЭДС, равную 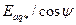 (см. рис. 10.28). Добавляя эту ЭДС к вектору
(см. рис. 10.28). Добавляя эту ЭДС к вектору  (или
(или 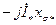 ), получают точку Д (см. рис. 10.27), через которую пройдет линия, совпадающая с направлением ЭДС
), получают точку Д (см. рис. 10.27), через которую пройдет линия, совпадающая с направлением ЭДС 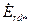 (или
(или 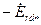 ). Угол между током
). Угол между током 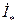 и этой линией является углом
и этой линией является углом 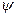 .
.
5. Опустив перпендикуляр из конца вектора 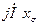 (или
(или 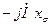 ) на линию 0Д, находят ЭДС
) на линию 0Д, находят ЭДС 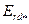 , наводимую в обмотке якоря результирующим потоком по продольной оси
, наводимую в обмотке якоря результирующим потоком по продольной оси 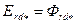 . Из характеристики
. Из характеристики 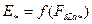 по
по 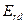 определяют МДС
определяют МДС 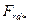 (см. рис. 10.28).
(см. рис. 10.28).
6. Определяют МДС продольной реакции якоря:
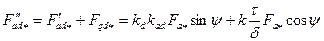 , (
, ( 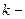 см. рис. 10.25)
см. рис. 10.25)
7. По сумме 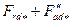 по характеристике
по характеристике 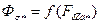 определяют поток рассеяния полюса
определяют поток рассеяния полюса 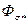 .
.
8. По потоку полюса 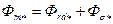 из характеристики
из характеристики 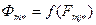 определяют сумму магнитных напряжений ротора
определяют сумму магнитных напряжений ротора  .
.
9. Находят МДС обмотки возбуждения при нагрузке в относительных единицах
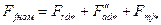
и в физических единицах (амперах)
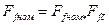 .
.
Из характеристики холостого хода 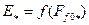 по
по 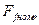 определяют ЭДС
определяют ЭДС 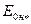 , наводимую в обмотке статора при холостом ходе, а затем находят изменение напряжения на выводах машины (для генератора):
, наводимую в обмотке статора при холостом ходе, а затем находят изменение напряжения на выводах машины (для генератора):
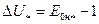 .
.
Дата добавления: 2017-05-02; просмотров: 1475;











