Временная сложность

Алгоритмы и сложность

Под сложностью некоторой задачи обычно подразумевают сложность алгоритмов, предназначенных для ее решения и реализуемых в виде вычислительных процедур на компьютерах. Понятие сложности алгоритма на интуитивном уровне чаще всего ассоциируется с его трудоемкостью, т. е. количеством некоторых условных операций, необходимых для завершения работы алгоритма, решающего задачу.

Различают меры сложности алгоритмов двух видов:

• статическая сложность, не зависящая от входных данных задачи;

• динамическая сложность, зависящая от входных данных задачи.

Типичным примером статической меры сложности алгоритма является длина программы, определяемая количеством операторов языка программирования, использованных для кодирования конкретной реализации алгоритма.

Динамическая мера сложности алгоритма дает информацию о потребностях алгоритма в ресурсах компьютера как функции входных данных задачи. Типичной динамической мерой сложности являются время вычислений или объем памяти, необходимой для реализации вычислений.

Следует заметить, что различные меры сложности используются в зависимости от условий применения. К тому же в реальных реализациях алгоритмов оценка времени вычислений и объема памяти, необходимой для реализации алгоритма, как правило, не являются независимыми: сокращение одной из них обычно достигается за счет возрастания другой.

Временная сложность

Временная сложность обычно является наиболее важным фактором, ограничивающим возможности современных решателей.

Временная сложность ‑ это число шагов (или элементарных операций) алгоритма 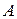, необходимых для нахождения решения некоторой задачи.. Для этой меры сложности определяются нижние и верхние границ сложности, оценки сложности в среднем, асимптотические оценки сложности, сложность модели вычислений и способа представления задачи.

Как правило, решается задача определения сложности вычислений для множества алгоритмов определенного класса. Например, ставится задача определения минимально возможного времени 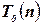упорядочения списка из 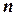объектов, расположенных в произвольном порядке. Понятно, что 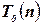является характеристикой задачи, а не конкретного алгоритма сортировки.

Значение функция 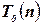показывает, что ни один алгоритм не может решить задачу сортировки менее, чем за 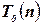единиц времени для произвольного списка объектов. С другой стороны, представляет интерес вычисление верхней границы 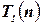, которая показывает, каковы максимальные затраты вычислительных ресурсов в наихудшем случае. Для многих алгоритмов неизвестны точные верхние и/или нижние оценок. Поэтому оказывается удобным при анализе алгоритмов подсчитывать только количество «элементарных» операций (шагов), а о сложности алгоритмов судить по асимптотике роста числа элементарных операций.

В теории сложности выделяют два фундаментальных класса алгоритмов:

• алгоритмы, сложность которых оценивается полиномом от размерности задачи;

• алгоритмы с экспоненциальной оценкой сложности.

Машина Тьюринга

Для теоретического анализа алгоритмов, реализующих методы решения задач дискретной оптимизации, используют математические модели вычислений, одной из которых является известная машина Тьюринга[1].

Машина Тьюринга ‑ это формализованное определение интуитивного понятия алгоритма, предполагающее, что всякому набору правил решения некоторой задачи, интуитивно понимаемому как алгоритм, соответствует некоторая машина Тьюринга.