Численные методы решения задач одномерной оптимизации многоэкстремальных функций
Метод ломаных
Положим х1 = а, x2 = b. Пусть вычисления проведены в точках 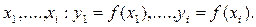 В силу условия Липшица
В силу условия Липшица
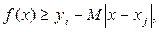
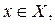
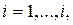
и потому

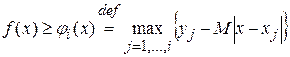 .
.
Нетрудно видеть, что функция 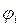 , является точной минорантой для функций, удовлетворяющих условию Липшица и принимающих в точках х1,..., хi значения соответственно y1, …, yi . Точка xi+1 выбирается по правилу
, является точной минорантой для функций, удовлетворяющих условию Липшица и принимающих в точках х1,..., хi значения соответственно y1, …, yi . Точка xi+1 выбирается по правилу
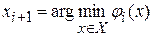 .
.
В качестве приближения к искомому значению минимума после N вычислений принимается величина 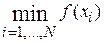 . Ясно, что после N вычислений погрешность метода не превосходит величины
. Ясно, что после N вычислений погрешность метода не превосходит величины
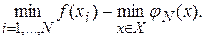
Число вычислений N может быть задано заранее. Если же требуется обеспечить отыскание значения минимума с точностью не хуже 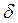 , то следует прекратить вычисления, как только
, то следует прекратить вычисления, как только
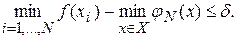
Метод покрытий
Пусть требуется обеспечить отыскание минимума с точностью не хуже 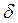 .
.
Обозначим через 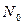 минимальное число отрезков длины r =2
минимальное число отрезков длины r =2 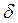 /М, которыми можно покрыть отрезок Х = [а, b]. Очевидно, что
/М, которыми можно покрыть отрезок Х = [а, b]. Очевидно, что 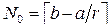 . Выберем
. Выберем
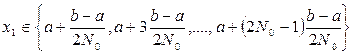 .
.
Нетрудно видеть, что отрезки длины r с центром в точках сетки (2.3) покрывают X.
Пусть вычисления проведены в точках 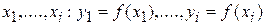 . Опишем (i+1)-й шаг алгоритма. Для этого введем обозначение
. Опишем (i+1)-й шаг алгоритма. Для этого введем обозначение
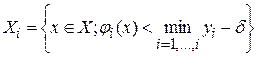 ,
,
где функция 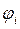 определена формулой (2.2). Ясно, что множество Xi является объединением не более i+l промежутков. Обозначим число этих промежутков через mi (на рис. 2.2 они выделены жирной линией). Пусть j-й промежуток есть
определена формулой (2.2). Ясно, что множество Xi является объединением не более i+l промежутков. Обозначим число этих промежутков через mi (на рис. 2.2 они выделены жирной линией). Пусть j-й промежуток есть 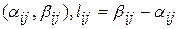 . Обозначим через Ni, минимальное число отрезков длины r, которыми можно покрыть множество Xi. Очевидно, что
. Обозначим через Ni, минимальное число отрезков длины r, которыми можно покрыть множество Xi. Очевидно, что
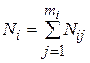 , где
, где 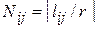 .
.
Выберем
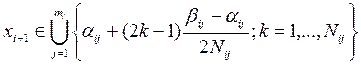 .
.
Ясно, что отрезки длины r с центрами в точках сетки (2.4) покрывают Xi.
Процесс останавливается на s-м шаге, если Хs = Æ. При этом величина 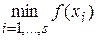 принимается в качестве приближения к значению минимума.
принимается в качестве приближения к значению минимума.
В силу пустоты множества Xs имеем 
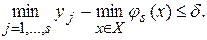
Это означает, что требуемая точность обеспечена, поскольку
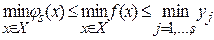 .
.
Дата добавления: 2022-05-27; просмотров: 146;











