Метод золотого сечения

Рассмотрим такое симметричное распо­ложение точек 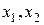на отрезке [а; b] , при котором одна из них ста­новится пробной точкой и на новом отрезке, полученном после иск­лючения части исходного отрезка. Использование таких точек позво­ляет на каждой итерации метода исключения отрезков, кроме первой, ограничиться определением только одного значения 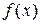, так как дру­гое значение уже найдено на одной из предыдущих итераций.

Точки 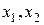которые обладают следующим свойством: каждая делит отрезок [а; b] на две неравные части так, что отношение длины всего отрезка к длине его большей части равно отношению длин большей и меньше частей отрезка. Точки с таким свойством на­зываются точками золотого сечения отрезка [а; b] . Это и объясняет название рассматриваемого метода.

Опишем алгоритм метода золотого сечения.

Шаг 1. Найти 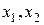по формулам 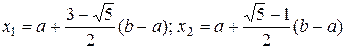. Вычислить 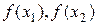. Положить .

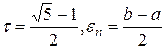Ш а г 2. Проверка на окончание поиска: если 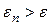, то перейти к шагу 3, иначе — к шагу 4.

Шаг 3. Переход к новому отрезку и новым пробным точкам. Если 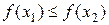, то положить 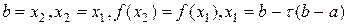и вычислить 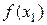, иначе — положить 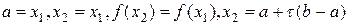и вычислить .

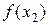Положить 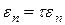и перейти к шагу 2.

Ш а г 4. Окончание поиска: положить .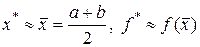

Метод парабол

Поиск точки минимума методами исключения отрезков основан на сравнении значений функции в двух точках. При таком сравнении раз­ности значений f(x) в этих точках не учитываются, важны только их знаки.

Учесть информацию, содержащуюся в относительных изменениях значений f(x) в пробных точках, позволяют методы полиномиальной ап­проксимации, основная идея которых состоит в том, что для функции f(x) строится аппроксимирующий многочлен и его точка минимума слу­жит приближением к х*. Для эффективного использования этих мето­дов на функцию f(x), кроме унимодальности, налагается дополнительное требование достаточной гладкости (по крайней мере, непрерывности).

Для повышения точности аппроксимации можно, во-первых, уве­личивать порядок полинома и, во-вторых, уменьшать длину отрезка аппроксимации. Первый путь приводит к быстрому усложнению вы­числительных процедур, поэтому на практике используются аппрок­симирующие полиномы не выше треть­его порядка. В то же время уменьше­ние отрезка, содержащего точку мини­мума унимодальной функции, не пред­ставляет особого труда.

В простейшем методе полиноми­альной аппроксимации — методе пара­бол используются полиномы второго порядка. На каждой итерации этого метода строится квадратный трехчлен, график которого (парабола) проходит через три выбранные точки графика функции f(x) (рис. 2).

Опишем метод парабол. Рассмотрим унимодальную на отрезке [а; b] функцию f(x) , достигающую минимума во внутренней точке этого отрезка. Выберем три точки 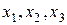отрезка [а; b] , для которых вы­полняются неравенства

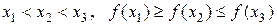(3)

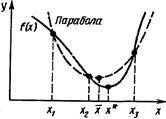
Рис. 2. Иллюстрация к мето­ду парабол

Из унимодальности f(x) следует, что 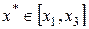. Построим квадратный трехчлен 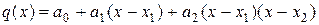, график которого проходит через точки 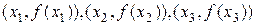графика функции f(x) . Будем считать, что хотя бы одно из неравенств (3) для 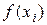является строгим (если 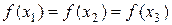, то поиск точки х * на этом закончен, так как из унимодальности функции f(x) следует, что она достигает минимума в каждой точке отрезка 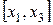). Тогда из (3) следует, что ветви искомой параболы направлены вверх, а точка минимума 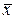трехчлена 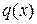принадлежит отрезку .

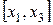Определяя коэффициенты 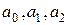из системы уравнений

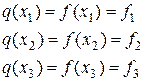
находим:

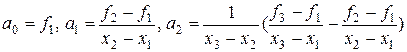
Точку минимума х квадратного трехчлена q(x) вычислим, прирав­няв его производную к нулю. Получим

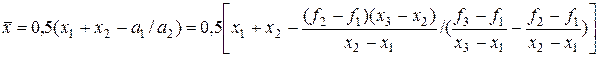(4)

Число х из (4) служит очередным приближением метода пара­бол к х *. Далее описанная процедура повторяется для новых точек 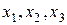, удовлетворяющих неравенствам (3).

Выбрать эти точки сред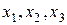и и 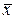можно с помощью перехо­да от исходного к новому отрезку 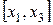, содержащему точку х *, ме­тодом исключения отрезков. Для этого перехода используются проб­ные точк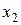и и 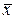и сравниваются значения 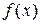в этих точках. Начало и конец нового отрезка, а также пробная точка, попавшая на него, об­разуют тройку точек, обладающих свойством (3).

Заметим, что на каждой итерации метода парабол, кроме первой, определяется только одно новое значение .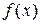

Условием окончания поиска служит близость к нулю разности 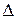чисел 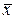, найденных на данной и предыдущей итерациях, т.е. неравен­ство 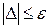|, где 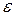— заданное число, характеризующее точность опре­деления х *.

Перечислим основные шаги алгоритма метода парабол.

Шаг 1. Выбрать точки 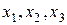, удовлетворяющие условиям (3). Перейти к шагу 2.

Ш а г 2. Найти х по формуле (4). На первой итерации перейти к шагу 4, на остальных — к шагу 3.

Ш а г 3. Проверка на окончание поиска. Сравнить модуль разно­сти значений х на данной и предыдущей итерациях 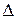с числом 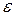. Если 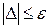, то поиск завершить, полагая 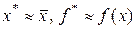, иначе — перейти к шагу 4.

Ш а г 4. Вычислить значение 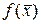. Перейти к шагу 5.

Шаг 5. Определить новую тройку чисел 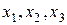. Присвоить 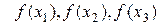соответствующие значения f(x), найденные ранее. Пе­рейти к шагу 2.