Принципы оптимального кодирования ОП абонентов

Данный раздел посвящен исследованию проблемы повышения эффективности кодового управления множественным доступом к связному ресурсу, что актуально для альтернативных приложений ЛВСРВ и ЛВСКО. Это обусловливается небольшими размерами передаваемых пакетов данных абонентами при занятии канала связи (а в ряде приложений, например в технологии ATM, и отказом от контроля передаваемых данных - контролируется только управляющая часть ячейки), что делает затраты времени на арбитраж даже при кодовом управлении множественным доступом к связному ресурсу сопоставимыми с продолжительностью взаимодействия абонентов при получении доступа к каналу связи.

Замечание. Здесь и далее говорим о кодировании ОП абонентов ЛВС, однако аналогично задача формулируется и решается при кодировании ОП заявок на обслуживание.

Ранее показано, что при кодовом управлении множественным доступом осуществляется арбитраж заявок по каждому разряду кода ОП 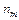, 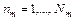(число которых при равномерном коде [ 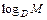] , где D - основание кода), на каждый из которых приходятся удельные затраты 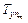, откуда получаем

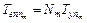(3.1)

Выражение (3.1) определяет альтернативные пути уменьшения затрат времени на управление множественным доступом при кодовом управлении 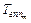, задаваемые изменением параметров 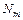и 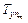. Первый из них может быть сформулирован в постановке задачи оптимального кодирования: для заданного вероятностного ансамбля { 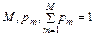} [4], где 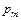- распределение вероятностей заявок на множестве M , найти множество кодов ОП длиной 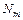, , 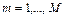обращающих в минимум среднюю скорость кодирования

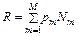
Для решения рассмотренной классической задачи теории информации может быть использован метод Хаффмена [4]. Альтернативный подход - снижение потерь 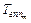за счет уменьшения 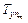связан с выбором механизма передачи прав на доступ к ресурсу между абонентами системы. Этот вопрос будет рассмотрен в следующем разделе.

Особенностью иной постановки задачи оптимального кодирования ОП будет необходимость учета более высокого приоритета уровня «1» над уровнем «0» (пусть исходно задали таким образом) в каждом разряде кода ОП, т.к. значением «1» в разряде кода приоритета абоненту предоставляется право занять ресурс, по значению «0» не предоставляется. Множество абонентов с заданной на нем вероятностью p требований общего ресурса, одинаковой для всех абонентов системы, называется математической моделью равномерного поэтапного кодирования/декодирования (или просто поэтапного кодирования) пользователей общих ресурсов: {M, N, 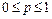, , 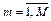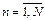}. Величина p здесь является характеристикой интенсивности поступления в систему требований ресурса.

Под величиной 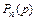будем понимать вероятность однозначного декодирования m-го абонента по n из N разрядам кода приоритета при вероятности p обращения абонентом к общему ресурсу системы. Рассмотрим изменение величины 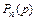при 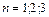, соответственно 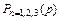при изменении p. Зависимости 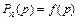для случая 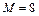представлены на рис. 3.1 (формула для расчетов 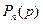приведена ниже), из которого следует, что при невысоких загрузках системы вероятность однозначного декодирования абонента не сильно изменяется с увеличением длины кодового слова, откуда может быть сделан вывод, что способ кодирования по всем N (имеется в виду равномерный код) разрядам кода приоритета в общем случае избыточен, особенно при малых загрузках системы.

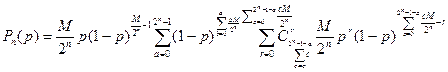
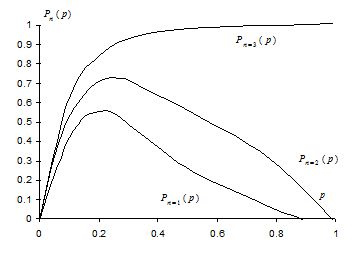
Рис. 3.1

Другими словами, выше рассмотрен принцип поэтапного кодирования, состоящий в управлении множественным доступом поэтапно - по частям кода приоритета, с увеличением длины кода на каждом этапе, и, как следствие, при возможности неоднозначного декодирования абонента по используемой части кода приоритета - на всех этапах, кроме последнего. Нетрудно показать, что скорость поэтапного кодирования максимальна при использовании всех N разрядов в коде приоритета.

Замечание. Особенностью реализации принципа поэтапного кодирования является возможность предоставления права занять ресурс одновременно нескольким абонентам, что требует обнаружения конфликта информации в канале, что, в свою очередь, будет являться условием необходимости увеличения длины кода приоритета. Принцип поэтапного кодирования предполагает конфликтную передачу прав между абонентами системы на занятие ресурса.

Влияние условия - ОП «1» над «0» при занятии ресурса, которое необходимо учитывать при кодировании приоритетов абонентов, рассмотрим на простом примере. Определим вероятность однозначного декодирования абонента по одному разряду кода приоритета (имеется в виду - только по первому разряду 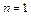, естественно в предположении, что здесь возможен конфликт), например для случая 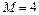, т.е. рассмотрим следующие кодовые комбинации «0011», «0001», «0111». Имеем: - для комбинации «0011» 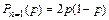, - для комбинации «0001» 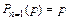, - для комбинации «0111» .

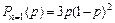Зависимости 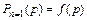для рассматриваемых случаев представлены на рис. 3.2, из которого могут быть сделаны следующие выводы.

1. Эффективность способа кодирования зависит от изменения p.

2. Могут иметь место интервалы изменения величины p, когда неравномерное кодирование абонентов (неравное число единиц и нулей в кодовой комбинации) эффективнее равномерного кодирования (соответственно, число нулей и единиц в кодовой комбинации совпадает).

Из рис. 3.2 в частности видим, что на интервале изменения параметра 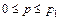эффективнее код «0111», на интервале изменения 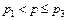- код «0011», на интервале изменения 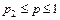- код «0001».

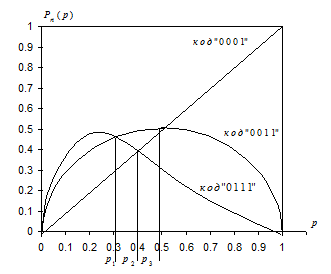
Рис. 3.2

Предельными случаями неравномерных кодов являются соответственно предельно неравномерные по «0» и по «1» коды, примеры которых для случая 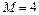представлены соответственно на рис. 3.3.а и 3.3.б, первый из которых эффективен при 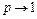, второй при 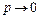, причем предельно неравномерный по «0» код обеспечивает поэтапный бесконфликтный арбитраж (бесконфликтное кодирование). Особенностью этих кодов будет максимальная эффективность соответственно при низкой и высокой загрузках системы. Другими словами, предельно неравномерные коды, по существу представляют собою предельные случаи кодирования, ориентированные, соответственно на низкую и высокую загрузки системы, и потому содержащие соответственно максимальное (по «1») и минимальное (по «0») число единиц в каждом кодовом слове кода, а любой применяемый

на практике неравномерный код будет занимать промежуточное положение между равномерным кодом ОП и соответствующим предельно неравномерным по «0» или по «1» кодом. Равномерный код отличается совпадением числа 1 и 0 в каждом кодовом слове.

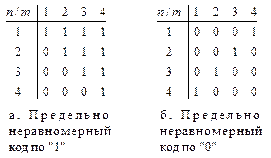
Рис. 3.3

Эффективность неравномерного поэтапного кодирования можно оценить по критерию «скорость однозначного поэтапного неравномерного кодирования по 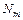разрядам»

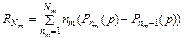
где 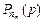- вероятность однозначного декодирования абонентов по разрядам 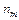кода ОП.

Под полной математической моделью поэтапного кодирования приоритетов абонентов понимается математическая модель равномерного поэтапного кодирования, учитывающая параметр 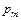или, соответственно, кодовая вероятностная модель, учитывающая параметр p. Или особенностью полной математической модели будет наличие уже двух параметров p и 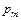различно влияющих на выбор оптимального способа кодирования: p - задает возможность эффективного поэтапного кодирования, в результате в качестве оптимального может быть получен неравномерный код; 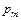- задает возможность эффективного полного кодирования, при этом в результате также в качестве оптимального может быть получен неравномерный код, причем в общем случае эти оптимальные неравномерные коды могут не совпадать.

В качестве критерия оптимальности также как и для модели поэтапного кодирования должен использоваться параметр 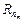, учитывающий параметр 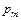: 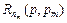- математическое ожидание скорости однозначного декодирования пользователя. Условием

оптимальности выбора способа кодирования будет 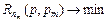или с учетом дискретности исходного набора альтернативных вариантов кодирования имеем

,

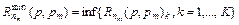где 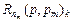- параметр 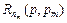для k-го способа кодирования из сравниваемого множества вариантов K, где

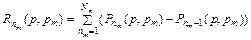
Заметим, что в отличие от соответствующих формул, приведенных ранее, здесь уже учитывается не только число единиц в кодовых комбинациях разряда кодов ОП абонентов, но и то, каким абонентам (соответственно, с какими значениями параметра 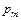) принадлежат значения единиц.

Утверждение. Всегда можно построить оптимальный код, который будет эффективнее случайного назначения кодов ОП.

Доказательство. Нетрудно показать, что метод случайного задания кодов ОП в среднем имеет характеристики обслуживания ниже, чем метод равномерного поэтапного кодирования, который неэффективен при низких и высоких загрузках системы. В области эффективного использования равномерного кода случайное задание кодов ОП неэффективно, т.к. не гарантирует однозначного декодирования абонента по 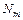разрядам кода.

Данное утверждение приведено с той целью, чтобы показать, что в рамках концепции кодового управления, в частности при оптимальном кодировании ОП абонентов, всегда можно получить конфликтный способ управления множественным доступом в реальном времени, который будет эффективнее для конкретных приложений, чем широко используемые в ЛВСОО случайные методы [8, 11], основным достоинством которых можно считать простоту реализации. Действительно, здесь не требуется поддерживать и, как следствие, восстанавливать в случае искажения какой-либо очереди передачи прав. Это делает данный метод, регламентируемый, например стандартами IEEE 802.3, TOP [8, 11] сегодня наиболее широко применяемым в ЛВСОО и ЛВССОО где отсутствуют жесткие ограничения на продолжительности обработки заявок.