При организации процессов электролиза с растворимыми анодами важно знать периодичность замены анодов. Для этого рассчитывается материальный баланс расходования анодов.
На растворимых анодах протекают реакции ионизации металлов под действием тока
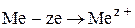 ,
,
а также возможны реакции химического растворения или переход компонентов анода в шлам (псевдореакции).
При составлении баланса расходования анодов компонентами системы будут являться металлы, входящие в состав анодов. Скорость растворения каждого из компонентов анода может быть рассчитана с помощью уравнения покомпонентного материального баланса (3.1), которое записывается следующим образом:
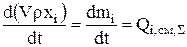 i=1…….k (3.22)
i=1…….k (3.22)
Здесь 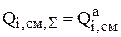 характеризует скорость растворения отдельных составляющих анода за счет различных реакций. Более подробно о способах расчета величины
характеризует скорость растворения отдельных составляющих анода за счет различных реакций. Более подробно о способах расчета величины 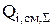 будет сказано позже. Однако, здесь необходимо заметить, что интенсивности металлов, растворяющихся на аноде
будет сказано позже. Однако, здесь необходимо заметить, что интенсивности металлов, растворяющихся на аноде 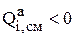 , так как их количество в анодах уменьшается.
, так как их количество в анодах уменьшается.
Если просуммировать уравнения 3.22 для всех компонентов анода, то суммарное уравнение материального баланса позволит определить скорость растворения анода массой ma:
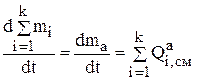 (3.23)
(3.23)
В уравнении 4.23 можно вместо производных записать конечные разности:
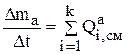 (3.24)
(3.24)
Тогда время замены анодов может быть рассчитано следующим образом:
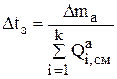 (3.25)
(3.25)
Поскольку масса анодов убывает, то 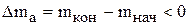 и интенсивности источников для компонентов анода
и интенсивности источников для компонентов анода 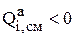 , то в выражении (3.25) время замены анодов получается величиной положительной.
, то в выражении (3.25) время замены анодов получается величиной положительной.
В технологическом регламенте определяется доля скрапа (kск), то есть доля анодных остатков. Тогда можно рассчитать массу анодов, которая должна раствориться до замены анодов, следующим образом:
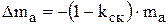 . (3.26)
. (3.26)
Первоначальная масса всех анодов зависит от массы одного анода (m1a) и их количества (na):
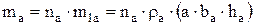 (3.27)
(3.27)
Здесь rа – плотность металла анода (кг/м3); ba – ширина анода (м), hа – высота погруженной части анодов (м), a – толщина анода (м).
После подстановки уравнений 3.26 и 3.27 в выражение 3.25 получается окончательное выражение для расчета времени замены анодов:
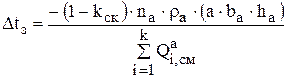 (3.28)
(3.28)
С помощью уравнения (3.22) могут также быть составлены и рассчитаны материальные балансы накопления катодного металла или шлама.
В практике электролитического рафинирования часто требуется узнать распределение компонентов анодного металла между катодом, электролитом и шламом. Для этого составляют баланс на единицу массы многокомпонентного анодного металла.
Первоначально необходимо получить информацию о всех электрохимических, химических реакциях и псевдореакциях (переход компонентов в шлам, раствор и включения частиц в катодный осадок), в которых участвуют металлы, входящие в состав анода. Далее необходимо рассчитать интенсивность перехода каждого из компонентов анода в раствор в результате протекания электрохимических и химических реакций 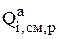 , в шлам
, в шлам 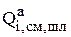 за счет псевдореакций, а также скорость их восстановления на катоде
за счет псевдореакций, а также скорость их восстановления на катоде 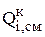 .
.
При составлении баланса распределения анодного металла по уравнению 3.25 рассчитывают время (Dtp), за которое будет израсходовано 1000 кг анодного металла с учетом выхода скрапа:
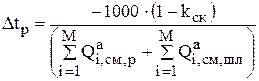 (3.29)
(3.29)
В знаменателе складываются суммарные источники для компонентов (i=1….M), участвующих в реакциях на аноде.
По известному времени Dtp с помощью уравнения (3.24) проводят расчет распределения компонентов анода. Масса компонентов, перешедших из анода в катод равна:
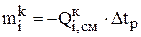 , (3.30)
, (3.30)
Знак минус означает, что данное количество вещества растворилось (ушло) с анода.
Количество i-го компонента, перешедшее из анода в шлам зависит от интенсивности этого перехода 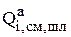 :
:
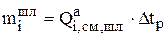 , (3.31)
, (3.31)
При расчете количества компонентов, перешедших с анода в раствор, необходимо учитывать как анодные, так и катодные реакции. За счет анодных реакций ионы металла переходят в раствор, а в результате восстановления на катоде их количество в растворе уменьшается. Тогда интенсивность перехода металла из анода в раствор равна:
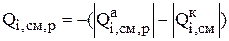 (3.32)
(3.32)
Соответственно масса металла, перешедшая в раствор за время Dtp равна:
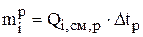 . (3.33)
. (3.33)
Затем можно рассчитать распределение i-го компонента, содержащегося в 1000 кг анодного металла, между катодом ( 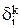 ), шламом (
), шламом ( 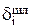 ) и раствором (
) и раствором ( 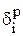 ) в процентах:
) в процентах:
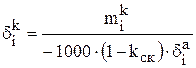 ;
;
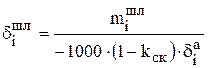 ;
;
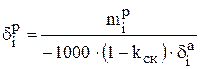 . (3.34)
. (3.34)
Здесь 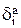 - содержание i-го компонента в аноде.
- содержание i-го компонента в аноде.
4.1.2. Стационарная модель материального баланса
При составлении стационарных математических моделей предполагается, что в системе никаких изменений (концентрации компонентов, объема электролита и т.д.) не происходит. Стационарную модель материального баланса имеет смысл составлять для электролизеров с непрерывной циркуляцией электролита.
Цель расчета стационарного материального баланса состоит в том, чтобы найти условия работы электролизера (например, состав и скорость потока циркуляции), при которых состав электролита в нем будет оставаться постоянным, соответствующим технологическому регламенту, несмотря на то, что на электродах протекают реакции, приводящие в изменению концентраций отдельных компонентов.
Система уравнений стационарного материального баланса для состава электролита выглядит следующим образом:
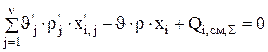 1…..k (3.35)
1…..k (3.35)
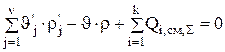 (3.36)
(3.36)
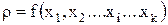 (3.37)
(3.37)
В большинстве гидроэлектрометаллургических производств входящий поток - это поток непрерывной циркуляции (n=1). Изменяя его состав и скорость можно добиться работы электролизера в оптимальном стационарном режиме. После небольших преобразований можно получить уравнения для расчета концентраций компонентов во входящем потоке
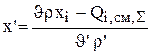 (3.38)
(3.38)
скорости входящего потока
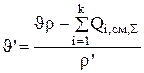 (3.39)
(3.39)
и плотности входящего потока
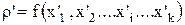 . (3.40)
. (3.40)
При расчете стационарного материального баланса режим технологического процесса, то есть состав электролита в ванне xi, его плотность rи скорость потока циркуляции на выходе из ванны 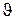 , должен быть известен.
, должен быть известен.
При расчетах материального баланса по уравнениям (3.38-3.40) величины 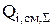 и вид зависимости плотности электролита от его состава должны быть предварительно рассчитаны или определены из литературы.
и вид зависимости плотности электролита от его состава должны быть предварительно рассчитаны или определены из литературы.
Если стационарный баланс составляется на определенную продолжительность работы (Dt) электролизера (час, сутки ит.п.), то можно рассчитать количество расходуемых реагентов за этот период. Для этого уравнение (3.35) умножим на интервал времени Dt и с учетом того, что 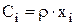 , получим выражение:
, получим выражение:
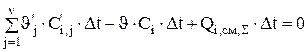 (3.41)
(3.41)
Если учесть, что количество каждого компонента, приходящего и уходящего из ванны за промежуток времени Dt, определяется соответственно соотношениями
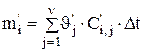 (3.42)
(3.42)
и 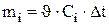 , (3.43)
, (3.43)
то из уравнения (3.34) получим
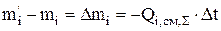 . (3.44)
. (3.44)
Рассчитав значения 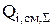 для всех компонентов можно определить, как вести процесс, чтобы состав электролита в ванне оставался неизменным. Положительное значение
для всех компонентов можно определить, как вести процесс, чтобы состав электролита в ванне оставался неизменным. Положительное значение 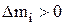 будет означать, что найденное по уравнению (3.44) количество вещества надо добавить за время Dt в электролит, а отрицательное значение
будет означать, что найденное по уравнению (3.44) количество вещества надо добавить за время Dt в электролит, а отрицательное значение 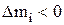 , указывает на необходимость отвода этого количества вещества. Таким образом, приходную часть баланса составляют
, указывает на необходимость отвода этого количества вещества. Таким образом, приходную часть баланса составляют 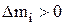 , а расходную
, а расходную 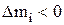 .
.
При составлении материального баланса на единицу массы одного из компонентов (n) определяют время расходования или образования этого компонента в количестве 100 или 1000 кг
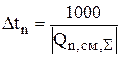 (3.45)
(3.45)
Зная расчетное время Dtn, определяют изменение массы остальных компонентов за этот промежуток времени по (3.45):
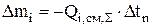 (3.46)
(3.46)
3.1.3. Источники вещества в электролизере
Компонентами материального баланса электролизера могут быть все составные части электролита (вода, соли, кислоты и т.д., ионы на которые эти соединения могут диссоциировать), а также исходные вещества и продукты реакций на электродах. Прежде чем рассчитывать материальный баланс электролизера, необходимо правильно выбрать компоненты баланса. Например, при составлении баланса расхода анодов составляющими баланса будут компоненты анода. При составлении баланса изменения состава электролита компонентами являются все вещества (либо ионы), растворенные в воде, вода, вещества (ионы), которые образуются в результате химических и электрохимических реакций на электродах.
Основную сложность в ходе расчета материального баланса представляет определение 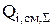 (кг/с) для всех компонентов. Суммарная интенсивность источника вещества по каждому компоненту учитывает все физико-химические процессы и реакции, в которых участвует данный компонент [16]. Поэтому необходимо правильно записать все реакции на аноде и катоде, а также возможные химические превращения, в которых участвуют компоненты.
(кг/с) для всех компонентов. Суммарная интенсивность источника вещества по каждому компоненту учитывает все физико-химические процессы и реакции, в которых участвует данный компонент [16]. Поэтому необходимо правильно записать все реакции на аноде и катоде, а также возможные химические превращения, в которых участвуют компоненты.
Суммарная интенсивность источника i-го компонента [16] складывается из скорости изменения количества вещества за счет химических ( 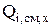 ) и электрохимических (
) и электрохимических ( 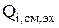 ) реакций, за счет явлений переноса (диффузия, фильтрация, миграция) (
) реакций, за счет явлений переноса (диффузия, фильтрация, миграция) ( 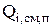 ), за счет перехода из одного агрегатного состояния в другое (
), за счет перехода из одного агрегатного состояния в другое ( 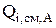 ):
):
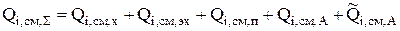 (3.47)
(3.47)
В уравнении (4.45) 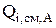 учитывает переход компонента из электролизера в окружающую среду (например, испарение воды с зеркала электролита), а
учитывает переход компонента из электролизера в окружающую среду (например, испарение воды с зеркала электролита), а 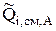 - обратный процесс перехода компонента из окружающей среды в электролизер (например, процесс конденсации паров воды из воздуха).
- обратный процесс перехода компонента из окружающей среды в электролизер (например, процесс конденсации паров воды из воздуха).
В общем случае все составляющие 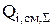 являются интегральными величинами и определяются локальной скоростью изменения количества вещества (
являются интегральными величинами и определяются локальной скоростью изменения количества вещества ( 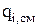 ,
, 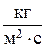 или
или 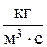 ) и величиной поверхности (S) либо объема (V), в котором происходит изменение количества компонента:
) и величиной поверхности (S) либо объема (V), в котором происходит изменение количества компонента:
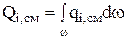 , где
, где 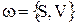 (3.48)
(3.48)
Если локальный источник вещества остается постоянным на всей поверхности (или во всем объеме), то можно воспользоваться более простым выражением:
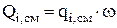 (3.49)
(3.49)
Расчет отдельных составляющих уравнения (3.47) определяется физической и химической природой процессов, приводящих к изменению количества того или иного компонента.
1. Скорость изменения количества вещества за счёт химической реакции ( 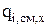 ) зависит от скорости реакции (
) зависит от скорости реакции ( 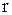 ),в которой участвует компонент, и его молекулярной массы (Mi):
),в которой участвует компонент, и его молекулярной массы (Mi):
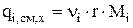 , (3.50)
, (3.50)
где ni - стехиометрический коэффициент i-го компонента. Так как 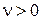 для продуктов реакции и
для продуктов реакции и 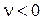 для исходных веществ то, в соответствии с уравнением (3.50),
для исходных веществ то, в соответствии с уравнением (3.50), 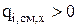 для компонентов, которые образуются в результате химической реакции и
для компонентов, которые образуются в результате химической реакции и 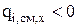 для тех, которые расходуются.
для тех, которые расходуются.
Если i-ый компонент участвует в нескольких химических реакциях, то локальный источник вещества за счет химических реакций будет представлять собой сумму:
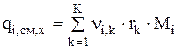 (3.51)
(3.51)
где 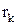 - скорость k-ой химической реакции; k=1…K – количество химических реакций, в который участвует i-ый компонент.
- скорость k-ой химической реакции; k=1…K – количество химических реакций, в который участвует i-ый компонент.
Если химическая реакция гетерогенная, то при расчете интегрального источника необходимо учитывать реакционную поверхность, а если гомогенная, то объем (ур.3.48, 3.49).
2. Скорость изменения количества вещества за счет электрохимической реакции ( 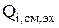 ) зависит от поверхности электрода (S):
) зависит от поверхности электрода (S):
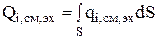 (3.52)
(3.52)
Локальная скорость изменения количества вещества за счет электрохимических реакций ( 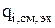 ) рассчитывается в соответствии с законом Фарадея:
) рассчитывается в соответствии с законом Фарадея:
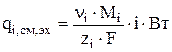 (3.53)
(3.53)
где Mi - молекулярная масса i-го компонента, кг/моль;
zi - число электронов, участвующих в реакции;
i - плотность тока, А/м2;
Вт - выход по току в долях единицы;
F=96500 Кл/моль - число Фарадея.
Если 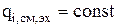 , то интегральный источник за счет электрохимической реакции зависит от величины токовой нагрузки (I):
, то интегральный источник за счет электрохимической реакции зависит от величины токовой нагрузки (I):
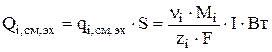 (3.54)
(3.54)
Часто один и тот же компонент участвует в нескольких электродных реакциях (например, катодной и анодной). В этом случае 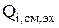 является суммой источников данного компонента по всем реакциям (k=1…K – количество электродных реакций, в которых участвует компонент):
является суммой источников данного компонента по всем реакциям (k=1…K – количество электродных реакций, в которых участвует компонент):
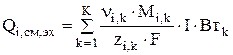 (3.55)
(3.55)
Подробнее об этом будет сказано при рассмотрении примеров составления материального баланса.
3. Скорость изменения количества компонента за счет явлений переноса
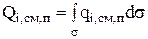 (3.56)
(3.56)
определяется локальной скоростью ( 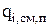 ) и размером поверхности (s), через которую осуществляется перенос.
) и размером поверхности (s), через которую осуществляется перенос.
Перенос компонентов возможен по трем основным механизмам:
диффузия, фильтрация и миграция. Эти явления приходится учитывать, если в электролизере есть пористая диафрагма, разделяющая
электродные пространства.
Локальная скорость изменения количества компонента за счет явлений диффузии определяется градиентом относительной концентрации компонента 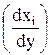 [15]:
[15]:
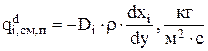 (3.57)
(3.57)
где у - направление нормали к поверхности переноса;
Di - коэффициент диффузии компонента, м2/с;
r - плотность электролита, кг/м3,
Если поток вещества направлен внутрь электролизера, то значения 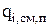 положительны, в противном случае
положительны, в противном случае 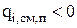 . В случае диффузии компонентов через пористую перегородку необходимо учесть снижение коэффициента диффузии в Кс раз (Кс - коэффициент сопротивления пористой перегородки) [15]:
. В случае диффузии компонентов через пористую перегородку необходимо учесть снижение коэффициента диффузии в Кс раз (Кс - коэффициент сопротивления пористой перегородки) [15]:
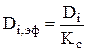
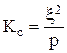 (3.58)
(3.58)
где x - коэффициент извилистости пор, 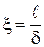 ;
; 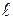 - длина поры, м;
- длина поры, м;
d - толщина пористой перегородки, м;
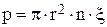 - доля свободного объема в пористой перегородке
- доля свободного объема в пористой перегородке
(n - количество пор на 1 м2, r - средний радиус поры, м).
Локальная скорость изменения количества вещества за счет фильтрации зависит от скорости фильтрации ( 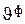 - объем раствора, который протекает в единицу времени через единицу поверхности пористой перегородки,
- объем раствора, который протекает в единицу времени через единицу поверхности пористой перегородки, 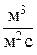 ), плотности раствора (r) и содержания в нем компонента хi [15]:
), плотности раствора (r) и содержания в нем компонента хi [15]:
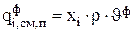 (3.59)
(3.59)
Скорость фильтрации рассчитывается по уравнению:
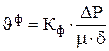 (3.60)
(3.60)
где 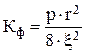 – коэффициент фильтрации, м2;
– коэффициент фильтрации, м2;
величины р, r, x - характеризует пористую перегородку и имеют тот же смысл, что и в уравнениях (4.58);
DP - перепад давлений по разные стороны перегородки, Па;
m - динамическая вязкость раствора, Па/с.
Перенос вещества по механизму миграции происходит под действием разности потенциалов электрического поля. Локальная интенсивность перемещения компонентов за счет миграции рассчитывается следующим образом [15]:
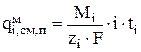 (3.61)
(3.61)
где i- плотность тока, А/м2; ti - число переноса i-го сорта ионов.
4. Изменение количества компонента за счет перехода его из одного агрегатного состояния в другое 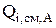 .
.
В водных растворах электролитов чаще всего реализуется агрегатный переход «газ – жидкость»: испарение воды или конденсация водяных паров. Испарение воды в электрохимических системах возможно за счет равновесного испарения и за счет конвективного уноса паров.
Равновесное испарение имеет место, когда газ насыщается парами воды до равновесного значения. Этот механизм реализуется в случае выделения газообразных продуктов на электродах или при барботаже электролита воздухом. При прохождении пузырьков газа через слой электролита они насыщаются парами воды до равновесия. При этом локальная скорость уноса воды, переносимой газом, рассчитывается по формуле [15]:
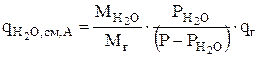 (3.62)
(3.62)
где 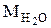 , Мг - молекулярные массы воды и газа, кг/моль;
, Мг - молекулярные массы воды и газа, кг/моль;
Р - атмосферное давление, кПа;
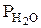 - парциальное давление паров воды при заданной температуре, кПа;
- парциальное давление паров воды при заданной температуре, кПа;
qг - скорость прохождения газа через электролит в расчете на 1м2 зеркала электролита, кг/(м2с).
В случае выделения газа на электродах величина qг рассчитывается в соответствии с законом Фарадея:
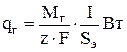 (3.63)
(3.63)
где I - ток, А; Sэ - площадь зеркала электролита, м2, z - число электронов, участвующих в электродной реакции.
Если в электролизёре применяется барботаж электролита газом
или воздухом, то [17]
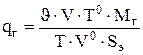 (3.64)
(3.64)
где 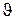 - объемный расход барботируемого газа,
- объемный расход барботируемого газа, 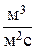 ;
;
V - объем ванны, м3;
Т0 - стандартная температура 273 К;
Т - температура электролита в электролизере. К;
V0= 0.0224 м3/моль - стандартный объем 1 моля газа.
Для расчета локальной интенсивности испарения за счет конвективного уноса используют эмпирическую формулу [15]
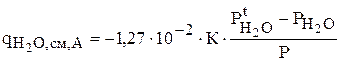 (3.65)
(3.65)
1,27×10-2 - коэффициент, характеризующий плотность потока испарения при температуре кипения раствора в сухой воздух, кг/(м2с);
К - безразмерный коэффициент, величина которого зависит от скорости движения воздуха;
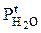 - парциальное давление паров воды над электролитом при температуре электролита;
- парциальное давление паров воды над электролитом при температуре электролита;
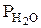 - парциальное давление паров воды при температуре внешней среды и данной влажности.
- парциальное давление паров воды при температуре внешней среды и данной влажности.
3.1.4. Зависимость плотности электролита от состава раствора
При составлении материального баланса необходимо знать зависимость плотности раствора от его состава. В основу расчета плотности электролита (r) была взята эмпирическая формула Здановского:
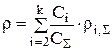 , (3.66)
, (3.66)
где Ci - концентрация i-го компонента в растворе, кг/м3; 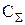 - суммарное солесодержание всех компонентов раствора, кроме воды;
- суммарное солесодержание всех компонентов раствора, кроме воды; 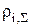 - плотность раствора i-го компонента при его содержании, равном
- плотность раствора i-го компонента при его содержании, равном 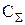 , кг/м3.
, кг/м3.
Суммирование в уравнении (3.66) ведется по всем компонентам раствора, кроме воды.
В справочниках [18] приводятся таблицы зависимостей плотности растворов отдельных веществ 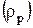 от их концентраций
от их концентраций 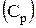 . Для многих растворов эти зависимости имеют линейный характер. Если учесть, что плотность воды равна 1000 кг/м3, то оказывается, что коэффициент
. Для многих растворов эти зависимости имеют линейный характер. Если учесть, что плотность воды равна 1000 кг/м3, то оказывается, что коэффициент 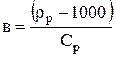 для многих веществ не зависит от концентрации. Тогда, в соответствии со справочным данным для любой концентрации i-го компонента раствора можно записать:
для многих веществ не зависит от концентрации. Тогда, в соответствии со справочным данным для любой концентрации i-го компонента раствора можно записать:
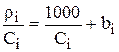 . (3.67)
. (3.67)
Аналогичное уравнение можно записать и для концентрации i-го компонента, равной суммарному солесодержанию всего раствора:
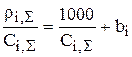 . (3.68)
. (3.68)
Если подставить (3.68) в (3.66), то
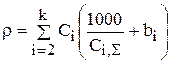 (3.69)
(3.69)
После небольших преобразований было получено выражение для зависимости плотности от состава раствора:
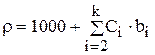 (3.70)
(3.70)
В уравнениях материального баланса (4.1) концентрация выражена массовой долей компонента (xi). Если учесть, что 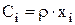 , то выражение (3.70) можно переписать:
, то выражение (3.70) можно переписать:
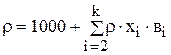 .
.
Их последнего уравнения было получено выражение зависимости плотности раствора от массовых долей растворенных в нем компонентов:
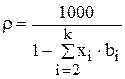 (3.71)
(3.71)
Если требуется рассчитать плотность электролита при другой температуре, необходимо воспользоваться еще одной эмпирической
формулой [19]
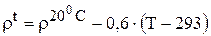 (3.72)
(3.72)
T - температура электролита, °K;
0,6 - эмпирический коэффициент, 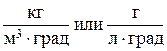 .
.
Дата добавления: 2016-06-05; просмотров: 3463;











