Особенности задач дискретной оптимизации. Общие сведения о методах решения задач: методы отсечения, комбинаторные методы, приближенные методы.
Выделим следующие (основные) методы решения задач дискретной оптимизации:
· методы отсечения для задач (частично) целочисленного линейного программирования;
· комбинаторные методы;
· приближенные методы.
Остановимся подробнее на этих методах.
1. Методы отсечения. Ранние попытки решения задач целочисленного линейного программирования сводились к отбрасыванию условия целочисленности, решению полученной задачи ЛП и округлению полученного решения. Можно привести простой пример, который показывает неприемлемость такого наивного подхода:
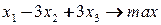
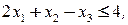
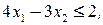
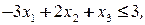
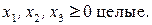
Игнорируя условие целочисленности, получим оптимальное решение линейной задачи 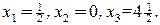 Никакие округления компонент этого решения не дают даже целочисленного плана. Оптимальное решение целочисленной задачи имеет вид
Никакие округления компонент этого решения не дают даже целочисленного плана. Оптимальное решение целочисленной задачи имеет вид 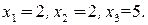
Основная идея методов отсечения, элементы алгоритма. Методы отсечения сводят решение этой задачи целочисленного линейного программирования к решению последовательности специальным образом построенных задач ЛП. Впервые эта идея для задач ЦЛП была высказана Данцигом. Она состоит в следующем. Если полученное решение удовлетворяет условию целочисленности, то процесс окончен. В противном случае к ограничениям исходной задачи добавляется новое линейное ограничение, обладающее двумя свойствами:
· полученное нецелочисленное решение ему не удовлетворяет;
· любое целочисленное решение ему удовлетворяет.
Далее решается задача ЛП с дополнительно введенным ограничением (отсечением), процесс повторяется до получения целочисленного решения. Реализация метода отсечения предполагает решение следующих трех проблем:
· нахождение универсального правила формирования отсечений;
· доказательство конечности процесса отсечения;
· борьба с чрезмерным ростом размерности задач при добавлении ограничений.
Р. Гомори удалось решить эти проблемы, что позволило ему создать универсальный и реализуемый в вычислительном отношении алгоритм.
Трудности вычислительной реализации. В дальнейшем выявилась большая непредсказуемость в поведении различных алгоритмов отсечения. Вычислительный эксперимент показал, что существуют задачи сравнительно небольшой размерности, решение которых не удается получить при больших затратах машинного времени. В дальнейшем было найдено объяснение этого явления: было показано[4], что для некоторых вариантов алгоритма Гомори существуют задачи, в которых число отсечений быстро растет с ростом размерности задачи и ростом коэффициентов, а в текущих симплекс-таблицах появляются весьма большие числа.
Методы отсечения не нашли широкого применения при решении прикладных задач ЦЛП по следующим причинам:
· сложно определить, какое отсечение (из большого их числа) является сильнейшим;
· методы отсечения приспособлены в основном для решения чисто целочисленных задач, которые составляют лишь малую часть задач ДО, встречающихся в приложениях;
· методы отсечения не приспособлены для решения разреженных задач ЦЛП.
Алгоритмы этого типа рассматриваются подробнее ниже, в разделе 7.1.
Комбинаторные методы. Основная идея комбинаторных методов состоит в использовании конечности множества  допустимых решений и замене полного их перебора сокращенным (направленным или неявным перебором). Если каким-либо образом удается показать, что подмножество
допустимых решений и замене полного их перебора сокращенным (направленным или неявным перебором). Если каким-либо образом удается показать, что подмножество 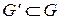 не содержит оптимальных решений, то в дальнейшем задача (1.1) решается на множестве
не содержит оптимальных решений, то в дальнейшем задача (1.1) решается на множестве  . Таким образом, главную роль в сокращении перебора играют оценка и отбрасывание неперспективных подмножеств, заведомо не содержащих оптимальных решений. Эта идея реализуется путем последовательного разбиения множества всех допустимых решений на подмножества. При этом среди подмножеств, последовательно порождаемых на каждом шаге процесса, могут обнаружиться как подмножества, не содержащие допустимых решений, так и подмножества, не содержащие оптимальных решений. Отбрасывание таких подмножеств позволяет заменить полный перебор частичным и тем самым уменьшает затраты вычислительных ресурсов.
. Таким образом, главную роль в сокращении перебора играют оценка и отбрасывание неперспективных подмножеств, заведомо не содержащих оптимальных решений. Эта идея реализуется путем последовательного разбиения множества всех допустимых решений на подмножества. При этом среди подмножеств, последовательно порождаемых на каждом шаге процесса, могут обнаружиться как подмножества, не содержащие допустимых решений, так и подмножества, не содержащие оптимальных решений. Отбрасывание таких подмножеств позволяет заменить полный перебор частичным и тем самым уменьшает затраты вычислительных ресурсов.
Таким образом, комбинаторные методы основаны на двух элементах:
· последовательное разбиение множества решений на подмножества;
· оценивание получаемых подмножеств и отбрасывание неперспективных.
Подмножество, которое не может быть отброшено, подвергается дальнейшему разбиению.
Комбинаторные методы различаются способом разбиения и способом оценивания, эти способы обычно связаны со спецификой решаемых классов задач. Правила, в соответствии с которыми производится отсев подмножеств, заведомо не содержащих оптимальных решений, называются правилами отсева.
Остановимся на классификации комбинаторных методов. Среди этих методов выделим следующие, наиболее часто применяемые при решении задач:
· метод последовательного анализа вариантов[5];
· метод ветвей и границ [10];
· локальные алгоритмы Ю.И. Журавлева [7];
· методы, основанные на последовательностных схемах[6];
· метод динамического программирования [20];
· аппроксимационно-комбинаторный метод[7];
Отметим, что универсальность комбинаторных методов обусловливает чрезвычайную широту их применения к конкретным задачам.
Приближенные методы. Эти методы широко применяются при решении задач ДО вида (1.1), так как нахождение точного решения может потребовать значительных вычислительных ресурсов. Современные приближенные методы обычно являются комбинированными, т.е. содержат в себе элементы различных методов. В приближенных методах решение задачи производится обычно в два этапа: построение начального решения и улучшение начального решения.
При этом на первом этапе широко используются эвристические алгоритмы ‑ алгоритмы, основанные на правдоподобных, но не обоснованных строго предположениях о свойствах оптимального решения задачи. Примером эвристического алгоритма может быть алгоритм решения задачи коммивояжера, в котором на каждом шаге реализуется переход в ближайшую из оставшихся точку. Алгоритмы такого типа носят название «greedy» («жадные» или пожирающие алгоритмы).
Эти алгоритмы на каждом шаге решают «локальную» задачу оптимизации; полученное решение может быть сколь угодно далеким от оптимума. На втором этапе используются алгоритмы локальной оптимизации, связанные с введенным понятием окрестности; при этом можно использовать несколько алгоритмов этого типа, изменяя правила выбора окрестности. Приближенным методам посвящен раздел 7.2 главы 7.
ЗАДАЧИ.
Задание. По данной текстовой формулировке задачи построить ее математическую модель в виде задачи целочисленного линейного программирования (ЦЛП). Найти решение задач ЦЛП с помощью системы моделирования AMPL.
Варианты заданий
1. В области выделены шесть городов, которые нуждаются в службе скорой помощи. Станции скорой помощи могут быть расположены в некоторых или во всех шести городах. Однако в силу территориальной близости некоторых городов одна станция может обслуживать более одного населенного пункта. Единственным условием является время поездки; оно не должно превышать 15 минут. Приведенная ниже таблица содержит время поездки в минутах между шестью городами.

Сформулируйте задачу в виде задачи ЦЛП, оптимальное решение которой определит наименьшее количество станций и их расположение. Найдите оптимальное решение, используя систему моделирования AMPL.
2. План музея, состоящего из нескольких комнат, соединенных открытыми дверями, показан на рисунке 1.2 ниже. Сторож, находящийся у двери, может наблюдать за двумя смежными комнатами. Администрация музея заинтересована, чтобы в каждой комнате присутствовал сторож, но число сторожей должно быть минимальным. Сформулируйте задачу в виде задачи ЦЛП и найдите ее оптимальное решение, используя систему моделирования AMPL.
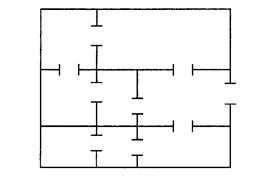
Рис. 1.2. План музея.
3. Игральная доска состоит из девяти равных квадратов, расположенных 3x3. Требуется заполнить каждый квадрат числом из интервала от 1 до 9 таким образом, чтобы сумма чисел каждой строки, каждого столбца и каждой диагонали была равна 15. Определите числа в каждом квадрате для следующих случаев.
a) Числа в каждой строке и каждом столбце различны.
b) Числа во всех квадратах различны.
Запишите сформулированную задачу в виде задачи ЦЛП с ограничениями и решите ее с помощью системы моделирования AMPL.
4. Станок используется для производства двух взаимозаменяемых видов продукции. Производительность станка позволяет за день изготовить не более 20 единиц продукции первого вида и 10 единиц второго вида. Существует альтернативная наладка станка, позволяющая ежедневно изготовлять не более 12 единиц продукции вида 1 и 22 единицы вида 2. Анализ рынка показывает, что максимальный суммарный спрос на два вида продукции составляет 35 единиц ежедневно. Предположим, что прибыль от производства единицы продукции первого и второго вида составляет 10 и 12 грн. соответственно. Какая из двух возможных настроек станка должна быть выбрана? Сформулируйте задачу в виде задачи ЦЛП и решите ее с помощью системы моделирования AMPL.
5. Рассмотрите задачу планирования производственной линии, связанной с изготовлением двух различных изделий на одном станке. Последовательность выполнения необходимых для этого восьми операций изображена на рисунке 1.3 ниже. Пусть Pj— время выполнения j-й операции (j= 1, 2,…, n). Сроки сдачи изделий типа 1 и 2, которые определяются на основе некоторого исходного момента, равны dl и d2 соответственно. Предполагается, что любая выполняемая на станке операция должна быть завершена до начала другой операции. Сформулируйте задачу в виде задачи частично-целочисленного линейного программирования.
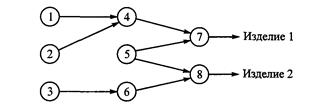
Рис. 1.3. Отношения предшествования операций для задачи 5.
6. Правая часть следующего ограничения может принимать одно из значений
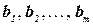 , т.е.
, т.е.
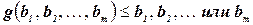 .
.
Покажите, как можно представить это ограничение с помощью бинарных переменных.
7. Имеются следующие слова, состоящие из трех букв: AFT, FAR, TVA, ADV, JOE, FIN, OSF и KEN. Буквам алфавита приписаны числа (метки), начиная с А = 1 и заканчивая Z = 26. Каждое слово помечается числом, равным сумме числовых меток составляющих его трех букв. Например, слово AFT имеет метку 1+ 6 +20 = 27. Необходимо выбрать пять из заданных восьми слов таким образом, чтобы получить максимальную суммарную метку. Вместе с тем выбранные пять слов должны удовлетворять следующему условию: (сумма меток первых букв) < (сумма меток вторых букв) < (сумма меток третьих букв).
Сформулируйте задачу в виде задачи ЦЛП и найдите ее оптимальное решение, используя систему моделирования AMPL.
8. Фирма, специализирующаяся на грамзаписи песен, заключила договор с восходящей звездой эстрады на запись восьми песен. Продолжительность песен равна 8, 3, 5, 5, 9, 6, 7 и 12 минут соответственно. Фирма планирует использовать для записи двусторонние кассеты. Каждая сторона имеет длительность звучания 30 минут. Фирма намерена распределить песни на две стороны кассеты сбалансированным образом. Это значит, что продолжительность звучания песен на каждой стороне кассеты должна быть примерно одинаковой (насколько это возможно). Сформулируйте задачу в виде задачи ЦЛП и найдите оптимальное решение.
9. Для обеспечения безопасности студентов отдел безопасности университета устанавливает телефоны экстренного вызова на территории студенческого городка. Отделу желательно установить минимальное количество телефонов таким образом, чтобы на каждой из основных улиц этого городка был расположен по крайней мере один телефон. На рисунке 1.4 ниже представлены основные улицы (от А до К) студенческого городка.
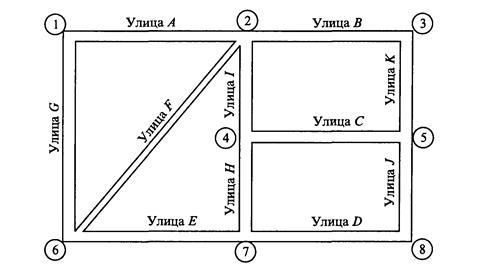
Рис. 1.4. Схема улиц студенческого городка.
Сформулируйте задачу в виде задачи ЦЛП и найдите оптимальное решение, используя систему моделирования AMPL.
10. Построить модель ЦЛП для задачи о распределении ресурсов между проектами с целью максимизации прибыли. Имеется четыре проекта, для реализации которых нужно вкладывать некоторые средства. Исходные данные содержатся в таблице ниже.
| Вложения в млн. грн. | Прибыль | |||
| 0,28 | 0,25 | 0,15 | 0,20 | |
| 0,45 | 0,41 | 0,25 | 0,35 | |
| 0,65 | 0,55 | 0,40 | 0,42 | |
| 0,78 | 0,65 | 0,50 | 0,48 | |
| 0,90 | 0,75 | 0,62 | 0,53 |
11. Фирме нужно составить расписание движения трех автомашин, обслуживающих восемь магазинов. Каждая машина может останавливаться у одного или нескольких магазинов, но ни в один магазин не допускается прибытия более одной машины. Определите число различных расписаний обслуживания магазинов.
12.Задача с постоянными платежами. Рассмотрим задачу
Минимизировать 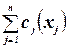
при ограничениях
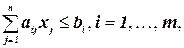
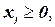
где
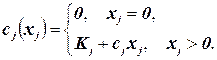
Величины 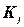 называются постоянными платежами. Покажите, как сформулировать эту задачу в виде частично целочисленной задачи линейного программирования.
называются постоянными платежами. Покажите, как сформулировать эту задачу в виде частично целочисленной задачи линейного программирования.
13.Сформулируйте задачу в терминах целочисленного программирования.
Максимизировать 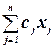
при ограничениях
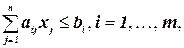
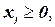
и выполняются либо три ограничения 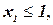
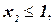
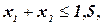 либо три ограничения
либо три ограничения 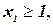
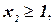
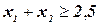 .
.
14.Сформулируйте задачу в терминах целочисленного программирования.
Максимизировать 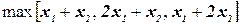
при ограничениях
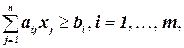
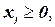
(т. е. найти значения 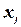 , удовлетворяющие ограничениям и обеспечивающие максимальное возможное значение трем указанным линейным функциям).
, удовлетворяющие ограничениям и обеспечивающие максимальное возможное значение трем указанным линейным функциям).
15.Рассмотрим задачу
Максимизировать 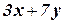
при ограничениях
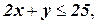
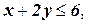
где 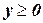 , а х может принимать только значения 0, 1, 4, 6. Сформулируйте и решите эквивалентную задачу в терминах целочисленного программирования.
, а х может принимать только значения 0, 1, 4, 6. Сформулируйте и решите эквивалентную задачу в терминах целочисленного программирования.
16.Сформулируйте постановку такой оптимизационной задачи. Студент университета решил в течение первого семестра прослушать лекции по пяти предметам, обозначенным А, В, С, D и Е. Каждый предмет читают в четырех группах, занимающихся в различное время. Обозначим через А1 группу 1, в которой читают предмет А, а через 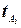 — начало занятий по этому предмету в данной группе. Для простоты предположим, что каждый предмет читают ежедневно, а занятия в группах начинаются в 8, 9, ..., 16 час. На выбор студента оказывает влияние время проведения занятий и репутация преподавателя. Пусть
— начало занятий по этому предмету в данной группе. Для простоты предположим, что каждый предмет читают ежедневно, а занятия в группах начинаются в 8, 9, ..., 16 час. На выбор студента оказывает влияние время проведения занятий и репутация преподавателя. Пусть 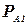 обозначает предпочтение, которое отдает студент предмету А в группе 1. К сожалению, он не может выбрать самое привлекательное, с его точки зрения, распределение предметов по группам в связи с перекрытием занятий во времени. Постройте модель выбора допустимого расписания, максимизирующего сумму оценок предпочтения студента.
обозначает предпочтение, которое отдает студент предмету А в группе 1. К сожалению, он не может выбрать самое привлекательное, с его точки зрения, распределение предметов по группам в связи с перекрытием занятий во времени. Постройте модель выбора допустимого расписания, максимизирующего сумму оценок предпочтения студента.
17.Фирма снабжает своими изделиями сеть небольших ресторанов, отпускающих обеды на дом. Фирма стремится обеспечить каждому владельцу такого ресторана достаточную прибыль. Рассматривается возможность размещения n новых точек подобного типа в крупном микрорайоне. По имеющейся оценке, размещение ресторана в пункте j обеспечит получение приемлемого дохода Rj при условии, что в радиусе 5 км от него аналогичная торговая точка отсутствует. Примем 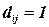 , если пункты i и j размещения ресторанов находятся в пределах радиуса 5 км, и
, если пункты i и j размещения ресторанов находятся в пределах радиуса 5 км, и 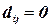 в противном случае. Фирма рассчитала все возможные
в противном случае. Фирма рассчитала все возможные 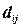 и стремится выбрать схему размещения новых ресторанов, обеспечивающую максимизацию общего дохода. Сформулируйте эту задачу в виде математической оптимизационной модели.
и стремится выбрать схему размещения новых ресторанов, обеспечивающую максимизацию общего дохода. Сформулируйте эту задачу в виде математической оптимизационной модели.
18. Баланс сборочной линии. Сборочная линия состоит из ряда рабочих мест, на каждом из которых можно в процессе сборки изделия выполнять одну или более операций. Всего нужно выполнить шесть операций и изделие проходит по сборочной линии, двигаясь от рабочего места 1 к рабочему месту 2, ... вплоть до последнего рабочего места. На каждую операцию затрачивается ti мин. Суммарное время выполнения всех операций на одном рабочем месте не должно превышать величины Т, называемой продолжительностью цикла линии. Примем в рассматриваемом примере Т = 10. Операции должны выполняться в определенном порядке. Отношение следования между операциями и их продолжительности заданы таблицей ниже. Оптимизационная задача заключается в минимизации числа рабочих мест при условии соблюдения заданной продолжительности цикла и сохранения заданного отношения следования. Постройте математическую оптимизационную модель этой задачи. (Указание: принять 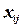 в качестве бинарной переменной, равной 1, если операция i выполняется на рабочем месте j. При осуществлении операций на каждом рабочем месте должен выполняться заданный порядок следования. Продолжительность выполнения всех операций на любом рабочем месте не должна превышать Т мин.)
в качестве бинарной переменной, равной 1, если операция i выполняется на рабочем месте j. При осуществлении операций на каждом рабочем месте должен выполняться заданный порядок следования. Продолжительность выполнения всех операций на любом рабочем месте не должна превышать Т мин.)

19. Построить математическую модель задачи выполнимости SAT, заданной в конъюнктивной нормальной форме, состоящей из 7 элементарных дизъюнкций 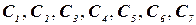 , называемых дизъюнктами:
, называемых дизъюнктами:
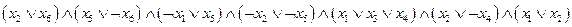 в виде задачи ДО.
в виде задачи ДО.
20. Построить модель линейного (одномерного) раскроя. Пусть имеется большое (практически неограниченное) число одномерных заготовок одинаковой длины L. Это могут быть трубы, прутки и т. п. Заготовки следует разрезать на полосы (детали) m типов; длина полосы типа i равна 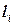 ,
, 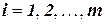 . По данным числам L и
. По данным числам L и  можно составить матрицу всевозможных способов раскроя
можно составить матрицу всевозможных способов раскроя 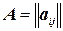 , где каждое
, где каждое 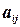 указывает количество полос типа i, получающееся из одной заготовки при раскрое ее по способу j,
указывает количество полос типа i, получающееся из одной заготовки при раскрое ее по способу j, 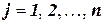 . Таким образом, каждый способ раскроя j изображается столбцом матрицы
. Таким образом, каждый способ раскроя j изображается столбцом матрицы 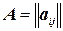 ; он характеризуется набором целых чисел
; он характеризуется набором целых чисел 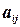 , подчиненных лишь условию
, подчиненных лишь условию 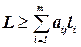 (суммарная длина выкраиваемых из заготовки полос не превосходит длины заготовки). Важно отметить, что матрица А этой задачи не задана изначально, а строится, быть может, уже в ходе решения задачи. Заданы потребности
(суммарная длина выкраиваемых из заготовки полос не превосходит длины заготовки). Важно отметить, что матрица А этой задачи не задана изначально, а строится, быть может, уже в ходе решения задачи. Заданы потребности 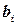 ,
, 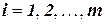 в полосах типа i. Требуется удовлетворить эти потребности, раскроив минимальное число заготовок. (Указание: введите переменные
в полосах типа i. Требуется удовлетворить эти потребности, раскроив минимальное число заготовок. (Указание: введите переменные 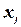 , означающие количество заготовок, подлежащее раскрою по способу j,
, означающие количество заготовок, подлежащее раскрою по способу j, 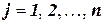 .
.
[1] Напомним, что в конце 50-х годов прошлого века, появились компьютеры, как инструмент, с помощью которого фактически стало возможно оптимизировать бизнес-процессы.
[2] В системе мобильной телефонной связи коммуникация между парами телефонов достигается за счет беспроводных соединений, использующих частоты из некоторой полосы. Задача назначения частот (ЗНЧ) (Frequency Assignment Problem (FAP)) является трудной дискретной задачей, тесно связанной с задачей раскраски графа.
[3] В [21] для решения этой задачи был использован оператор элиминации ‑ резолюция, которая по двум дизъюнктам 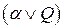 и
и 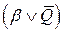 выводит дизъюнкт
выводит дизъюнкт 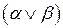 , называемый резольвентой, в которой литерал
, называемый резольвентой, в которой литерал 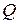 элиминирован. Оператор элиминации (в данном случае ‑ резолюция) порождает новые дизъюнкты, которым соответствуют новые ребра в графе взаимосвязей.
элиминирован. Оператор элиминации (в данном случае ‑ резолюция) порождает новые дизъюнкты, которым соответствуют новые ребра в графе взаимосвязей.
[4] Финкелъштейн Ю. Ю. Приближенные методы и прикладные задачи дискретного программирования. — М.: Наука, 1976.
[5] Михалевич В. С. Последовательные алгоритмы оптимизации и их применение. 1. // Кибернетика. 1965. № 1. С. 45-56; П. // Кибернетика. 1965. № 2. С. 85-88.
[6] Емеличев В. А., Комлик В. И. Метод построения последовательности планов для решения задач дискретной оптимизации. — М.: Наука, 1981. – 208 с.
[7] Хачатуров В. Р., Веселовский В. Е., Злотов А. В. и др. Комбинаторные методы и алгоритмы решения задач дискретной оптимизации большой размерности. ‑ М.: Наука, 2000. ‑ 354 с.
Дата добавления: 2016-06-05; просмотров: 3915;











