Приведённый момент инерции

Приведённым моментом инерции механизма называется момент инерции условного диска, которым заменяется реальный механизм, обладающего кинетической энергией, равной сумме кинетических энергий всех звеньев механизма.

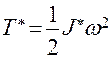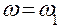Кинетическая энергия условного диска , где , т. е. угловая скорость звена приведения, равная угловой скорости кривошипа.

Кинетическая энергия звена, совершающего поступательное движени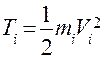е, , где 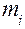– масса звена, 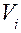– скорость звена.

Кинетическая энергия звена, совершающего вращательное движени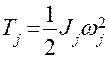е, , где 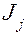– момент инерции звена, 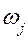– угловая скорость звена.

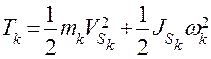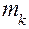Кинетическая энергия звена в плоскопараллельном движении , где – масса звена, 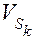– скорость центра масс звена, 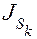– момент инерции звена относительно его центра масс, 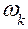– угловая скорость звена. Согласно определению имеем:

.

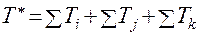Подставив сюда записанные выше выражения кинетических энергий и, решая затем полученное равенство относительно 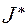, запишем

.

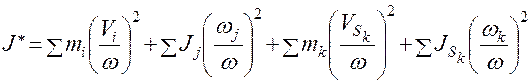Как видно из этой формулы, приведённый момент инерции зависит от структуры механизма, от массовых характеристик звеньев, от положения механизма и не зависит от угловой скорости ведущего звена. Некоторые механизмы имеют постоянное значение приведённого момента инерции. Машины, в основе которых механизмы с 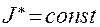, называются ротативными.