Построение сетевой модели
Структура сетевой модели и оценки продолжительности работ (в сутках) заданы в табл. 3. Требуется:
а) получить все характеристики СМ;
б) оценить вероятность выполнения всего комплекса работ за 35 дней, за 30 дней;
в) оценить максимально возможный срок выполнения всего комплекса работ с надежностью 95% (т. е. 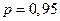 ).
).
Три первые графы табл. 3. содержат исходные данные, а две последние графы - результаты расчетов по формулам. Так, например,
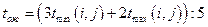 ,
,
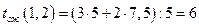 ,
,
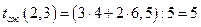 ,
,
……………………………….
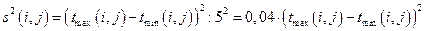 ,
,
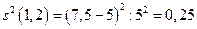 ,
,
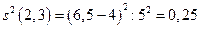 .
.
| Работа | Продолжительность | Ожидаемая | Дисперсия | |
| 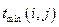
| 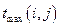
| Продолжительность 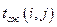
| 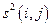
|
| (1.2) | 7.5 | 0.25 | ||
| (2.3) | 6.5 | 0.25 | ||
| (2.4) | 1.00 | |||
| (2.5) | 5.5 | 0.25 | ||
| (3.7) | 0.5 | 3.5 | 0.36 | |
| (4.5) | 7.5 | 0.25 | ||
| (4.6) | 5.5 | 0.25 | ||
| (4.9) | 1.00 | |||
| (5.8) | 4.5 | 0.25 | ||
| (5.10) | 1.00 | |||
| (6.9) | 0.00 | |||
| (6.11) | 1.00 | |||
| (7.10) | 1.00 | |||
| (8.10) | 1.00 | |||
| (9.10) | 1.00 | |||
| (10.11) | 10.5 | 0.25 |
Получим сетевую модель аналогичную рассматриваемой во второй главе:
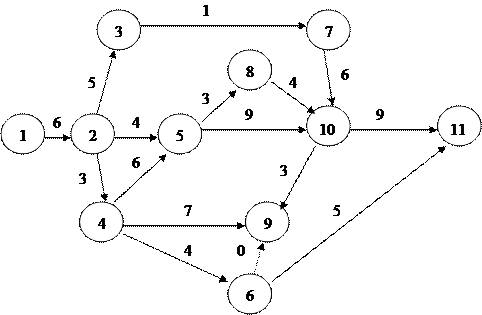
Таким образом, ход расчета характеристик модели остается аналогичен рассмотренному ранее. Причём критическим является путь: 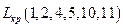 , а его продолжительность равна
, а его продолжительность равна 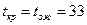 дня.
дня.
Дисперсия критического пути составляет:
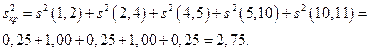
Для использования формулы показателя дисперсии необходимо иметь среднее квадратическое отклонение, вычисляемое путем извлечения из значения дисперсии квадратного корня, т. е. 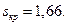 Тогда
Тогда
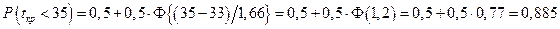 ,
,
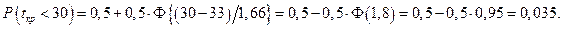
Таким образом, вероятность того, что весь комплекс работ будет выполнен не более чем за 35 дней, составляет 88,5%, в то время как вероятность его выполнения за 30 дней - всего 3,5% .
Для решения второй (по существу обратной) задачи прежде всего в табл.2 найдем значение аргумента z, которое соответствует заданной вероятности 95% . В графе 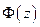 наиболее близкое значение (0,9545
наиболее близкое значение (0,9545  100%) к ней соответствует
100%) к ней соответствует 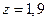 . В этой связи в формуле (3.61) используется именно это (не совсем точное) значение. Получаем:
. В этой связи в формуле (3.61) используется именно это (не совсем точное) значение. Получаем:
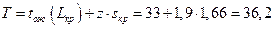 дня.
дня.
Следовательно, максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 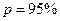 составляет 36,2 дня.
составляет 36,2 дня.
Составим словесно-формульное описание алгоритма
1. Начало процесса.
2. Ввод данных 
3. Организация цикла
4. Вычисление для каждого значения работы: 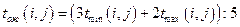
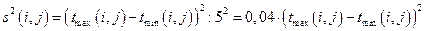 .
.
5. Завершение цикла.
6. Вычисление дисперсии критического пути 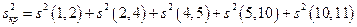 .
.
7. Вычисление вероятности выполнения работ за 35 и 30 дней
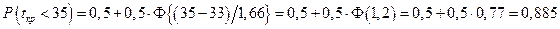 ,
,
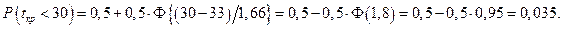
8. Организация цикла для нахождения  .
.
9. Завершение цикла.
10. Вычисление срока выполнения всего комплекса работ 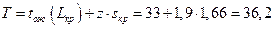 .
.
11. Вывод результатов.
12. Конец процесса.
Дата добавления: 2017-04-05; просмотров: 1717;











