Модели целочисленного линейного программирования

Если компонентами решения задачи линейного программирования должны быть целыми числами, то такая задача называется задачей целочисленного линейного программирования. В экономике это часто связанно с неделимостью продукции.

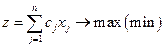
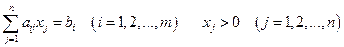
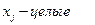
Существует несколько способов решения задач целочисленного линейного программирования.

Метод отсечения.

Суть метода состоит в том, что сначала решается задача линейного программирования без условия целочисленности. Если полученный ответ удовлетворяет условию целочисленности, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:

- оно должно быть линейным;

- оно должно отсекать найденный оптимальный нецелочисленный план;

- оно не должно отсекать ни одного целочисленного плана.

Такие ограничения называются правильными отсечениями.

После введения нового ограничения вновь решается задача линейного программирования. Если вновь полученный план целочисленный то задача решена. Если это не так, то к задаче добавляется новое ограничение. Процесс повторяется до тех пор, пока полученный оптимальный план не будет полностью целочисленным.

Геометрический смысл добавления каждого нового линейного ограничения состоит в проведении дополнительной прямой (гиперплоскости), которая отсекает от многоугольника (многогранника) допустимых решений его часть вместе с оптимальной точкой с нецелыми координатами. В отсекаемую часть не должна попасть ни одна точка с целыми координатами. В результате новый многогранник решений содержит все точки с целыми координатами, содержавшиеся в первоначальном многограннике решений. Следовательно, полученное при этом многограннике оптимальное решение будет целочисленным.

Пример.

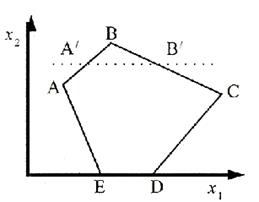
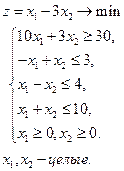
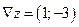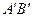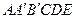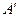Построим область допустимых решений задачи. Это многоугольник АВСДЕ. Построим вектор градиент целевой функции . Ясно, что точкой оптимума будет точка В(3.5; 6.5). Полученное решение не удовлетворяет условию целочисленности. Проведем прямую , отсекающую точку В и не отсекающую ни одну целую точку. Получаем новый многоугольник , где и 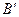имеют целые координаты. Точка 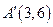новое решение задачи целочисленного программирования.

Метод Гомори.

Пусть задача линейного программирования имеет оптимальное решение. Не нарушая общности задачи предположим, что 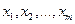- базисные переменные, полученные на последнем шаге симплекс-метода. Они выражены через небазисные переменные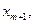

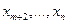
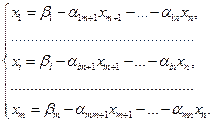
Оптимальное решение задачи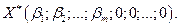

Пусть в этом оптимальном решении 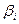- не целая компонента.