Уравнение неразрывности
Основные понятия гидродинамики
Гидродинамика – это раздел гидравлики, в котором изучаются закономерности движения жидкости.
Гидродинамика, или динамика жидкости, существенно отличается от динамики твердого тела. Отдельные частицы твердого тела жестко связаны друг с другом, а в движущейся жидкой среде такие связи отсутствуют, жидкая среда состоит из множества частиц, движущихся одна относительно другой. Законы гидродинамики, определяющие закономерности движения жидкости, сложнее законов покоящейся жидкости. В покоящейся жидкости существует лишь одна характерная величина – гидростатическое давление. При движении состояние жидкости определяется не только давлением, но и величинами и направлением скоростей и ускорений отдельных частиц жидкости. Скорости в данной точке пространства, занятого движущейся жидкостью, являются в общем случае функциями координат этой точки и времени.
Задача гидродинамики – установление связи в движущемся потоке между давлением и кинематическими характеристиками потока. Величины скорости и давления могут изменяться в зависимости от времени и координат рассматриваемой точки.
Вспомним введенное ранее понятие идеальной жидкости – это такая воображаемая жидкость, которая совершенно лишена вязкости. В такой невязкой идеальной жидкости возможен лишь один вид внутренних напряжений – нормальные напряжения сжатия, то есть гидромеханическое давление или просто давление. Давление в движущейся идеальной жидкости обладает теми же свойствами, что и в неподвижной жидкости:
· на внешней поверхности жидкости давление направлено по внутренней нормали;
· в любой точке внутри жидкости давление по всем направлениям одинаково.
При рассмотрении движения жидкости различают установившееся и неустановившееся движение.
Если скорость и давление зависят только от координат, то есть в любой точке потока несжимаемой жидкости эти величины с течением времени остаются неизменными, то такое движение называется установившимся. При установившемся движении скорость и давление являются функцией только координат точки:
u = f (x, y, z)и p = f (x, y, z).
Пример установившегося движения – течение воды по трубопроводу при постоянном напоре.
Если давление и скорость в потоке зависят не только от координат, но и от времени, то есть
u = f (t, x, y, z)и p = f (t, x, y, z).
то такое движение называется неустановившимся.
Примерами неустановившегося движения могут быть – разгон или торможение жидкости в трубах при включении (выключении) насосов, истечение воды при опорожнении резервуара через отверстие и т. п.
Установившееся движение бывает равномерныминеравномерным.
Равномерным называется движение, при котором скорости жидкости не меняются и с течением времени, и по длине потока, то есть в сходственных точках поперечных сечений скорости одинаковы по всей длине потока.
Если при движении скорости жидкости, не изменяясь во времени, меняются по длине потока, то такое установившееся движение называется неравномерным. Такой характер движения бывает при сужении или расширении потока в реке, на повороте, в конфузорах и диффузорах.
Напорным называется такое движение, при котором поток со всех сторон ограничен твердыми, жесткими направляющими стенками. Обычно это – движение жидкости в трубах при полном их заполнении (водопроводы, нефтепроводы). Такое движение происходит за счет избыточного давления, создаваемого насосом или водонапорным баком.
Движение, при котором поток лишь частично ограничен твердыми стенками и имеет свободную поверхность, называется безнапорным. Например, течение в реках, водосливных лотках, канализационных трубах. Давление на свободной поверхности обычно равно атмосферному. Движение в таких потоках происходит за счет геометрического уклона русла, то есть под действием силы тяжести.
Введем еще некоторые определения.
Совокупность или геометрическое место точек, через которые последовательно проходит жидкая частица при своем движении, называется траекторией частицы.
При установившемся движении траектории частиц жидкости являются неизменными во времени.
При неустановившемся течении траектории различных частиц, проходящих через данную точку пространства, могут иметь разную форму.
Линия тока–это линия, касательная к которой в любой точке совпадает с направлением вектора скорости частиц жидкости в данный момент времени (рис. 3.1).
Из определения понятно, что если некая кривая является линией тока, то это справедливо лишь для данного момента времени. Со временем линия тока меняет форму. Через каждую точку пространства может проходить лишь одна линия тока, которая с течением времени может изменять свою форму и свое положение. Совокупность линий тока для какого-то момента времени рассматриваемого движения называется спектром линий тока.
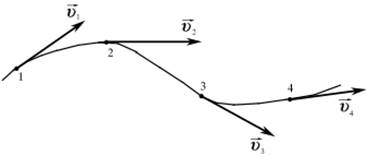
Рис. 3.1
При установившемся движении линии тока не меняются во времени.
Более того, при установившемся движении линии тока и траектории движения частиц совпадают.
Действительно, пусть в некоторой точке пространства скорость жидкой частицы в момент t0 имеет значение u0. Построим линию тока, проходящую через эту точку. Отложим на векторе u0 малый отрезок Δs1 и из его конца построим вектор u1, соответствующий этой точке пространства. Затем на этом векторе отложим отрезок Δs2 и аналогично построим вектор u2 и т. д. (рис. 3.2).
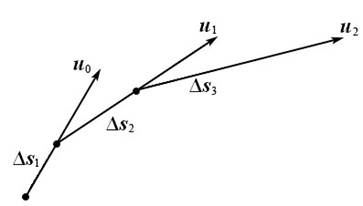
Рис. 3.2
Подчеркнем, что все построение выполняется для одного фиксированного момента времени t0, поэтому сейчас безразлично, является ли течение установившимся или неустановившимся. Если отрезки Δsi примем достаточно малыми, то приближенно получим кривую, близкую к линии тока.
Попробуем построить так же траекторию жидкой частицы, которая в момент времени t0 находилась в исходной точке. Из этой точки за малое время Δt1 частица проходит путь Δs1. Приближенно его можно считать совпадающим с направлением вектора u0. Если движение установившееся, то скорость в конце отрезка Δs1 будет такой же, как и в момент времени t0. Тогда далее частица начнет перемещаться по направлению вектора u1 и пройдет путь Δs2 и т. д. Очевидно, что при установившемся движении траектория совпадет с линией тока. Если же движение неустановившееся, то за время Δt1, за которое частица пройдет отрезок Δs1, скорость в конце отрезка изменится и не будет равна u1 ни по величине, ни по направлению. Тогда из конца отрезка Δs1 жидкая частица пойдет по другой траектории, не совпадающей с линией тока.
Возьмем для фиксированного момента времени в жидкой среде замкнутый контур l (рис. 3.3). Каждая точка этого контура, представляющая собой жидкую частицу, в последующие моменты времени перемещается в пространстве, заполненном жидкостью.
Часть жидкости, ограниченная поверхностью траекторий точек замкнутого контура, называется струей.

|
|
| Рис. 3.3 | Рис. 3.4 |
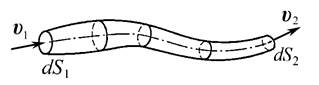
Проведем через каждую точку контура l линию тока (рис. 3.4). Совокупность этих линий тока образует трубчатую поверхность, выделяющую часть жидкой среды и называемую трубкой тока.
В случае установившегося движения траектории совпадают с линиями тока и, следовательно, трубка тока совпадает со струей.
Если уменьшать размеры замкнутого контура, то часть потока, заключенная внутри трубки тока станет элементарной струйкой, то есть такой струйкой, в поперечном сечении которой скорости можно считать одинаковыми.
При установившемся движении:
· элементарная струйка не меняет своей формы и ориентации в пространстве;
· нормальные составляющие скорости на линии тока равны нулю, следовательно, перетекания жидкости через боковую поверхность данной струйки нет, и трубку тока можно рассматривать как трубку с непроницаемыми стенками;
· нормальные сечения струйки dS1, dS2 (рис. 3.4) малы, но не одинаковы в разных сечениях, поэтому пучок линий тока внутри трубки может сгущаться и расширяться;
· так как поперечные сечения струйки малы, скорости во всех точках таких сечений можно считать одинаковыми, однако при переходе от одного сечения к другому они изменяются.
При дальнейшем стремлении поперечных размеров струйки к нулю она в пределе стягивается в линию тока.
Перетекания жидкости из одной струйки тока в другую нет, элементарная струйка представляет собой самостоятельный элементарный поток. Таким образом, жидкость втекает во входное отверстие струйки тока и вытекает через выходное, не проникая через ее боковые поверхности. Потоки конечных размеров можно рассматривать как совокупность элементарных струек, то есть предполагать течение струйным. Из-за различия скоростей струйки будут как бы скользить одна по другой, но перемешиваться не будут.
Введение таких представлений дает возможность использовать для элементарной струйки математический аппарат дифференциального исчисления и интегрирования по всему сечению потока для получения уравнений и закономерностей движения жидкости.
Движение жидкости, при котором линии тока являются строго параллельными прямыми, будем называть параллельноструйным. На практике часто встречаются течения, отличные от параллельноструйных.
Плавно изменяющееся движение – это движение, близкое к параллельноструйному, при котором радиус кривизны линий тока достаточно велик, а угол, образованный крайними линиями тока рассматриваемого потока (или элементарной струйки), близок к нулю (угол θ,рис. 3.5).
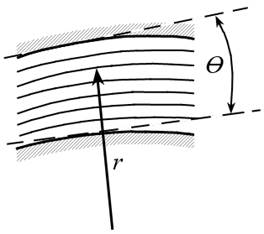
Рис. 3.5
Назовем живым сечением потока поверхность, проведенную перпендикулярно линиям тока и находящуюся внутри потока. Поскольку распределение скоростей в потоках в общем случае неравномерно, линии тока в них не параллельны друг другу и живые сечения представляют собой криволинейные поверхности. Например, при движении жидкости в конически расходящейся трубе (рис. 3.6), когда поток состоит из расходящихся элементарных струек, живое сечение представляет собой криволинейную поверхность ABC. Если линии тока в потоке будут параллельными (течение параллельноструйное), живое сечение будет плоским.
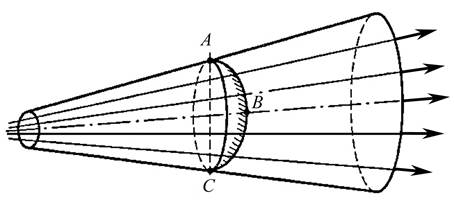
Рис. 3.6
Живое сечение может быть ограничено твердыми стенками полностью или частично.
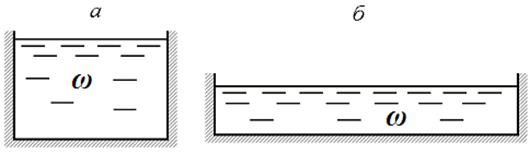
Рис. 3.7
Величина живого сечения определяется его площадью. Однако условия течения жидкости зависят не только от площади живого сечения, но и от его формы. На рис. 3.7 представлены поперечные сечения двух каналов. Хотя живые сечения обоих каналов представляют собой прямоугольники с равновеликими площадями, очевидно, что условия движения жидкости по ним будут разными из-за неодинакового отношения глубины к ширине потока.
Длина линии поперечного сечения, по которой жидкость соприкасается с твердой границей потока, называется смоченным периметром. При напорном течении жидкости, когда поток со всех сторон ограничен твердыми стенками, смоченный периметр будет равен полному периметру живого сечения. В случае безнапорного течения часть периметра поперечного сечения потока, приходящаяся на свободную поверхность жидкости, не включается в расчет смоченного периметра.
Для трубы радиуса r, полностью заполненной жидкостью, смоченный периметр равен (рис. 3.8.а)
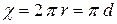 .
.
В случае безнапорного течения в канале прямоугольного поперечного сечения (рис. 3.8.б)
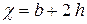 .
.
a
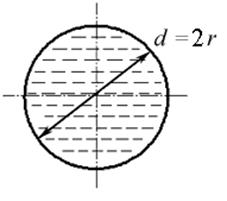
| б
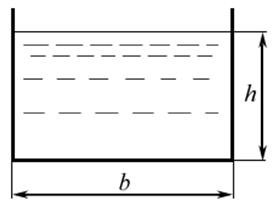
|
| Рис. 3.8 |
Отношение площади сечения потока жидкости ω к смоченному периметру 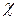 называется гидравлическим радиусом R.
называется гидравлическим радиусом R.
Для напорного потока в круглой трубе (рис. 3.8.а)
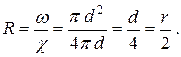
Для безнапорного потока (рис. 3.8.б)
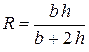 .
.
Из этой формулы понятно, что гидравлический радиус канала а на рис. 3.7 больше гидравлического радиуса канала б.
Расходом называют количество жидкости (в объемных или весовых единицах), протекающее через поперечное (живое) сечение потока в единицу времени. В зависимости от того, в каких единицах определяется количество жидкости, различают объемный Q, весовой Qв и массовый Qм расходы. Зависимость между ними следующая
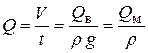
где V – количество (объем) жидкости;
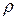 – плотность жидкости;
– плотность жидкости;
g – ускорение свободного падения.
В гидравлике чаще всего используют объемный расход, далее под термином «расход» будем понимать именно объемный расход, если специально не оговорим иное.
Рассмотрим движение жидкости на участке элементарной струйки (рис. 3.9). Частичка жидкости перемещается от сечения 1 к сечению 2 за промежуток времени dt, проходя при этом расстояние l. Поскольку стенки трубки тока непроницаемы для движущейся жидкости, количество жидкости, прошедшее через сечение 1 за время dt будет равным объему цилиндра:
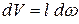 ,
,
где dω – площадь живого сечения струйки.
Элементарный объемный расход, то есть количество жидкости, проходящее в единицу времени через живое сечение элементарной струйки, определится как
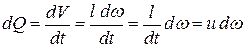 .
.
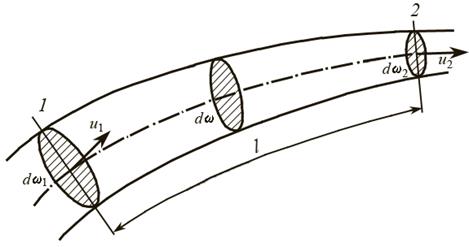
Рис. 3.9
Если рассматривать поток жидкости как совокупность элементарных струек, то общий расход потока определится как сумма элементарных расходов отдельных струек:
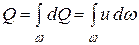 .
.
Чтобы вычислить расход по этой формуле, нужно знать распределение скорости движения жидкости во всех точках живого сечения (рис. 3.10).
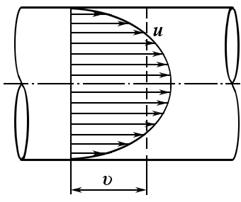
Рис. 3.10
Чтобы упростить расчеты для практического применения, вводится понятие средней скорости потока. Средняя скорость в сечении 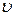 – это скорость, с которой данное сечение должны проходить все частицы жидкости, чтобы расход Q для этого сечения был равен действительному расходу при неравномерном распределении скоростей по сечению.
– это скорость, с которой данное сечение должны проходить все частицы жидкости, чтобы расход Q для этого сечения был равен действительному расходу при неравномерном распределении скоростей по сечению.
Тогда уравнение расхода для полного потока запишется как
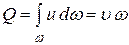 ,
,
где: 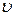 – средняя по сечению скорость жидкости.
– средняя по сечению скорость жидкости.
Среднюю скорость тогда можно определить как
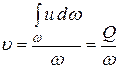 .
.
Средняя скорость по живому сечению – абстрактное понятие, введенное для упрощения изучения движения жидкости.
Уравнение неразрывности
Уравнение неразрывности как для элементарной струйки, так и для всего потока – это математическое выражение условия сплошности потока при установившемся течении жидкости.
Выделим в потоке элементарную струйку (рис. 3.11).
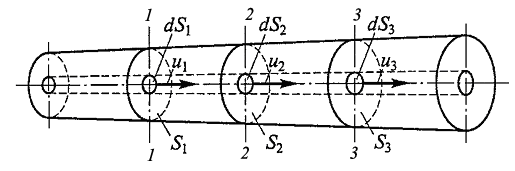
Рис. 3.11
Рассмотрим участок между сечениями 1–1 и 2–2. За время dt внутрь этого участка через сечение 1–1 войдет количество жидкости, равное объему цилиндра с площадью основания dS1 и образующей u1dt. Через сечение 2–2 за это же время вытечет объем жидкости, равный 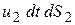 . Отметим следующие обстоятельства:
. Отметим следующие обстоятельства:
· через боковые поверхности элементарной струйки жидкость не проникает (таково свойство трубки тока);
· жидкость несжимаема и в ней отсутствуют пустоты и разрывы.
Это означает, что будет справедливым равенство
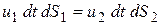 ,
,
откуда
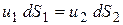 . .
| (3.1) |
Для других сечений будут справедливы такие же соотношения:
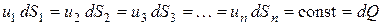 .
.
Это уравнение (3.1) и выражает условие неразрывности элементарной струйки, из него следует, что через все сечения струйки проходит одинаковый расход жидкости. Из уравнения понятно, что
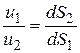 ,
,
то есть скорости течения в разных сечениях элементарной струйки обратно пропорциональны площадям этих сечений.
Для полного потока уравнение неразрывности можно получить, проинтегрировав уравнение (3.1) по площадям соответствующих сечений полного потока (рис. 3.11):
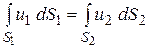 .
.
Используя понятие средней скорости по сечению
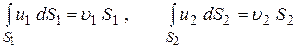 ,
,
можно записать
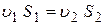 . .
| (3.2) |
Так как сечения 1–1 и 2–2 выбраны произвольно, то и для любых других сечений это равенство будет справедливо.
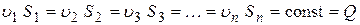 . .
| (3.3) |
Уравнения (3.2) и (3.3) и есть уравнения неразрывности полного потока. Они показывают, что объемный расход несжимаемой жидкости при установившемся движении остается постоянным вдоль всего потока.
Из уравнения (3.2) следует, что средние скорости потока обратно пропорциональны площадям соответствующих живых сечений:
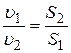 .
.
Уравнение Бернулли
Дата добавления: 2017-04-05; просмотров: 5288;










