Поверхностное натяжение

Силы притяжения молекул внутри объема жидкости взаимно уравновешиваются и проявляются только на границах – на твердых стенках, на свободной поверхности. На свободной поверхности из-за того, что сила притяжения со стороны молекул воздуха значительно меньше, чем сила взаимного притяжения молекул жидкости, появляется результирующая сила, направленная внутрь объема. Молекулы поверхностного слоя находятся в особом напряженном состоянии, образуется как бы тонкая упругая пленка, возникает поверхностное натяжение. Энергия поверхностных молекул отличается от энергии молекул, расположенных в объеме. Суммарная величина этой «поверхностной» энергии 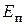пропорциональна площади поверхности S раздела сред:

.

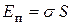Коэффициент пропорциональности 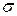, входящий в эту зависимость, получил название коэффициента поверхностного натяжения. Величина его зависит от природы соприкасающихся сред, степени чистоты жидкости и ее температуры.

Коэффициент поверхностного натяжения можно также представить соотношением

,

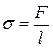где F – сила поверхностного натяжения;

l – длина линии раздела сред.

Из этого определения видно, что коэффициент поверхностного натяжения – это сила, действующая на единицу длины линии раздела сред и направленная по касательной к поверхности жидкости.

Единица измерения поверхностного натяжения в СИ [σ]= Н/м, в технической системе – кГ/м.

Величина коэффициента поверхностного натяжения жидкостей небольшая. Например, для воды при температуре Т = +20º С оно составляет около 7 Г/м. Именно поэтому силы поверхностного натяжения в гидравлике обычно не учитываются.

Молекулярное давление, определяющее величину поверхностного натяжения, зависит от кривизны поверхности раздела жидкой и газообразной сред. Оно становится заметным только при малых размерах объемов жидкости, например, в капиллярных трубках. Именно благодаря поверхностному натяжению, жидкость, смачивающая поверхность стенок капиллярных трубок, образует вогнутый мениск и подтягивается вверх: силы сцепления между молекулами твердой поверхности стенок и молекулами жидкости выше молекулярных сил взаимодействия внутри жидкости. В случае несмачиваемой поверхности в капиллярной трубке устанавливается выпуклый мениск, и жидкость в трубке опускается: силы взаимодействия между стенкой и жидкостью меньше внутренних сил взаимодействия в жидкости.

Вязкость

Очень важным для гидравлики физическим свойством жидкости является вязкость – свойство жидкости оказывать сопротивление движению слоев жидкости относительно друг друга.

Вследствие молекулярного взаимодействия в жидкости возникают силы внутреннего трения: слой, движущийся быстрее, увлекает за собой слой, движущийся медленнее, а тот, в свою очередь, тормозит слой, движущийся быстрее. Таким образом, вязкость проявляется в виде возникновения силы трения при перемещении (сдвиге) слоев жидкости друг относительно друга. Другими словами, вязкость – это свойство, обусловливающее возникновение в жидкости при ее движении касательных напряжений.

И. Ньютон предложил гипотезу о том, что сила F вязкости (трения) между двумя соседними слоями жидкости с площадью соприкасания ω равна

,

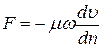где μ – динамический коэффициент вязкости;

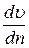– поперечный градиент скорости движения жидкости;

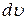– скорость смещения слоев жидкости друг относительно друга;

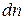– расстояние между осями соседних слоев жидкости.

Знак «минус» в формуле указывает на то, что сила трения направлена противоположно направлению движения.

Размерность динамического коэффициента вязкости в СИ [μ] = Н·с/м² (Па∙с). В системе СГС единица динамической вязкости 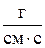называется пуаз в честь французского ученого А. Пуазейля.

Динамический коэффициент вязкости (динамическая вязкость) зависит от природы жидкости и температуры. С повышением температуры жидкости коэффициент вязкости μ уменьшается.

Если силу трения между слоями отнести к площади соприкосновения слоев, то полученная удельная сила трения называется касательным напряжением:

.

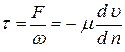Наряду с динамическим коэффициентом вязкости, в гидравлике широко используется кинематический коэффициент вязкости ν, представляющий отношение μ к плотности ρ:

,

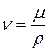который имеет размерность в СИ и технической системе 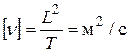. До 1980 года допускалось измерение кинематической вязкости в стоксах (названных так в честь английского гидромеханика Дж. Стокса): 1 Ст = 1 см²/с.

Вязкость играет очень важную роль в процессе движения жидкостей. В природе мало жидкостей, вязкость которых меньше, чем вязкость воды, но существует много жидкостей с большой вязкостью (масла, нефть), есть очень вязкие жидкости (глицерин, патока).

Идеальная жидкость. В гидравлике часто используется и большую роль играет понятие «идеальной» жидкости.

Под идеальной жидкостью понимается жидкость, частицы которой обладают абсолютной подвижностью, то есть идеальная жидкость не имеет вязкости, не испытывает температурного расширения и абсолютно несжимаема. Введение в рассмотрение подобной научной абстракции вместо реальной жидкости упрощает решение ряда гидравлических задач, позволяет широко использовать математические методы, проводить обобщения и аналогии. Такой подход научно обоснован и является полезным и плодотворным. Конечно, при применении получаемых для идеальной жидкости решений и выводов в конкретных обстоятельствах приходится вносить необходимые поправки и дополнения, которые следуют из практики и учитывают реальные условия. Однако, как показал опыт, получаемые таким образом картины течения достаточно хорошо согласуются с реальными процессами.