Нелинейные авторегрессионные модели

Покажем как к некоторому классу нелинейных систем можно применить метод наименьших квадратов.

Полиномиальная множественная регрессионная модель

Система описывается уравнением

Y = A₀ + A₁ · X₁ + A₂ · X₂ + A₃ · X₁ · X₂ + A₄ · X₁ · X₁ + A₅ · X₂ · X₂. (12)

Обозначим: Z₁ = X₁ · X₂; Z₂ = X₁ · X₁; Z₃ = X₂ · X₂ и подставим эти выражения в предыдущую формулу:

Y = A₀ + A₁ · X₁ + A₂ · X₂ + A₃ · Z₁ + A₄ · Z₂ + A₅ · Z₃.

Итак, система (12) приведена к линейной регрессии, которая затем идентифицируется стандартным образом.

Мультипликативная регрессионная модель

Рассмотрим систему

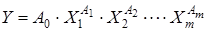. (13)

Прологарифмируем левую и правую части данного уравнения:

ln(Y) = ln(A₀) + A₁ · ln(X₁) + A₂ · ln(X₂) + … + A_m · ln(X_m).

Обозначим:

W = ln(Y), B₀ = ln(A₀), Z₁ = ln(X₁), Z₂ = ln(X₂), …, Z_m = ln(X_m).

Получим:

W = B₀ + A₁ · Z₁ + A₂ · Z₂ + … + A_m · Z_m.

Далее применяем VYR и получаем оценки параметров.

Обратная регрессионная модель

Y = k/(A₀ + A₁X₁ + … + A_mX_m).

Заменим: W = 1/Y, a_i = A_i/k. И перейдем к линейной множественной модели:

W = a₀ + a₁ · X₁ + … + a_m · X_m.

Экспоненциальная модель

Y = e^B₀ ^{+ B}₁^X₁ ^{+ B}₂^X₂ ^{+ … + B}_m^X_m.

Прологарифмируем левую и правую части уравнения:

ln(Y) = B₀ + B₁ · X₁ + B₂ · X₂ + … + B_m · X_m.

Выполним замену W = ln(Y) и получим:

W = B₀ + B₁ · X₁ + B₂ · X₂ + … + B_m · X_m.

Далее пользуемся выражением для линейной множественной модели.

Итак, рассмотрены методы идентификации дискретных статических и динамических систем на классе регрессионных моделей.

Рассмотрим теперь информационные технологии, позволяющие решать рассмотренные задачи.

Синтез регрессионных моделей с помощью Microsoft Excel

Так как основным объектом анализа и обработки в системах идентификации является информационное множество, которое содержит экспериментальные данные и представляется в виде таблицы, то задачу идентификации проще всего решать в среде Excel.

Для синтеза регрессионных моделей в Microsoft Excel могут применяться различные средства, выбор которых зависит от класса объекта, который можно описать парной или множественной регрессией. Все их можно разбить на две группы.

1. Графический метод получения регрессии — применяется только случая парной модели.

2. Автоматические методы оценивания параметров регрессии. Эта группа основана на применении встроенных функций Excel и модуля Анализ данных.