Задачи о положениях манипуляторов.

При решении задач проектирования и управления промышлен­ными роботами приходится определять как положения его звеньев относительно неподвижной системы координат (абсолютные поло­жения звеньев), так и их относительные положения (например, обобщенные координаты). Соответственно эти задачи известны в робототехнике как прямая и обратная задачи о положениях.

Рис 25.1

Для исследования движения исполнительного механизма мани­пулятора в пространстве наибольшее распространение получил ме­тод преобразования координат с матричной формой записи. Он позволяет упорядочить выполняемые действия и сократить матема­тические выкладки. При этом ме'годе выбирают число систем коор­динат, равное числу элементов звеньев, образующих кинематические пары. Неподвижная система координат обычно связывается со стойкой, а с каждой кинематической парой связыва­ется подвижная система координат, одна из осей которой связана с характерными признаками звена, например осевой линией. Для

Рис 25.1

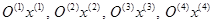примера на рис.24.2, а показаны координатные оси , (или 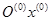) четырехзвенной открытой кинематичес­кой цепи из звеньев 1, 2, 3, 4, моделирующей структуру руки человека (см. рис. 24.2, б). Ось 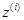направляют вдоль оси кинематической пары, а ось 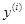дополняет правую систему координат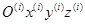

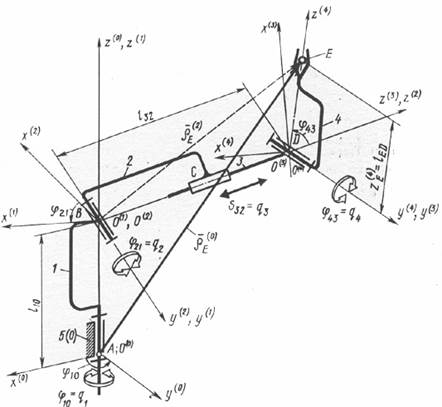
Применение метода преобразования координат для решения прямой задачи о положениях проиллюстрируем на примере кинема­тической схемы промышленного робота (рис. 25.1). Четыре подви­жных звена 1, 2, 3 и 4 образуют четыре одноподвижные пары, из которых три вращательные и одна поступательная. Число степеней подвижности робота равно четырем:

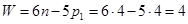
Поэтому для решения прямой задачи о положениях должны быть заданы четыре обобщенные координаты: относительные углы поворота звеньев 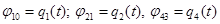и относительное перемещение вдоль оси звена 3 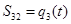(рис. 25.1).

Требуется определить радиус-вектор 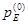точки Е схвата относительно неподвижной системы координат 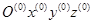, связанной со стойкой 5 (или 0). Оси систем координат ориентированы относите­льно элементов кинематических пар следующим образом:

ось 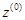неподвижной системы координат стоики направлена вдоль оси вращательной пары А;

со звеном 1 связана система 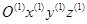, имеющая смещение 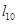начала координат 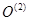вдоль оси 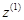. Ось 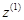совпадает с осью 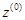, а ось 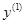направлена по оси вращательной кинематической пары В;

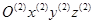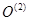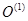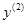со звеном 2 связана система , имеющая начало координат совпадающее с точкой . Ось совпадает с осью 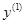т. е. с осью вращательной кинематической пары В;

начало координат системы 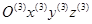имеет смещение 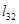относительно точки 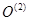вдоль оси 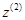. Ось 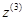выбрана совпадающей с осью ;

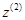координата 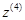точки Е схвата 4 задана в системе 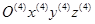, ось 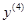которой направлена по оси вращательной кинематической пары D.

Для определения радиуса-вектора 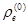необходимо разрешить матричное уравнение перехода к системе координат :

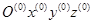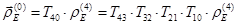(25.1)

Достоинство метода проявляется в случае специального выбора подвижных систем координат. Если координатные оси совмещать с осью вращательной пары или направлением поступательной па­ры, то матрицы перехода существенно упрощаются.

Координаты точки Е в трехмерном пространстве записываются в виде столбцевых матриц:

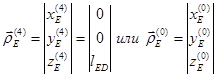
Здесь 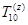- матрица перехода от системы 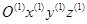к системе 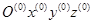(элементарная матрица поворота вокруг оси z и перемещения вдоль оси z):

;

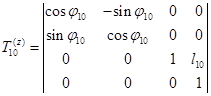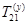- матрица перехода от системы 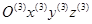к системе 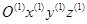(элементарная матрица поворота относительно оси y):

;

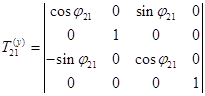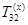- матрица перехода от системы 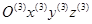к системе 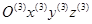(элементарная матрица перемезения вдоль оси x):

;

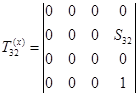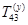- матрица перехода от системы 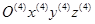к системе 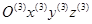(элементарная матрица поворота вокруг оси x):

.

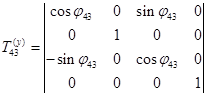Подставив эти матрицы в формулу (25.1), получим координаты точки Е в системе 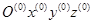. Развернутые формулы, определя­ющие положение точки Е схвата, ввиду громоздкости не приведены. При решении конкретных задач на ЭВМ целесообразно восполь­зоваться библиотекой стандартных подпрограмм для выполнения элементарных операций с матрицами.

Для определения скорости и ускорения точек звеньев простран­ственных механизмов манипуляторов при использовании метода преобразования координат имеют в виду, что радиус-вектор 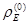, например, точки Е есть векторная функция обобщенных координат:

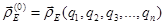
поэтому скорость 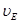точки Е определяется по соотношению

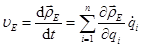, (25.2)

или

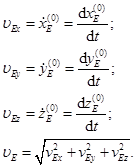(25.3)

Абсолютную угловую скорость j-го звена относительно стойки находят сложением угловых скоростей при относительном движе­нии звеньев:

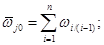(25.4)

индекс i(i - 1) указывает на порядковые номера звеньев, участву­ющих в относительном движении, например

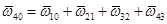
Решения обратных задач о положениях манипуляторов в явном виде имеют важное значение как при проектировании, так и при управлении. При проектировании такие решения позволяют оце­нить влияние конструктивных параметров на процесс движения, при управлении - построить быстродействующие алгоритмы управле­ния.

Контрольные вопросы к лекциям 24, 25

1. Что такое манипулятор, автооператор, промышленный робот?

2. Для чего предназначены промышленные роботы?

3. В чём заключаются особенности структуры кинематических цепей манипуляторов промышленных роботов?

4. От чего зависят двигательные возможности манипулятора промышленного робота?

5. Что такое подвижность манипулятора ? Как она определяется?

6. Дайте определение рабочего пространства, зоны обслуживания манипулятора и его маневренности (на любом примере)