по двум положениям звеньев

Кривошипно-ползунный механизм. Для центрального кривошипно-ползунного механизма (внеосность e = 0, рис. 4.5, а) ход ползуна 3 (его максимальное перемещение) равен удвоенной длине кривошипа: h = 2l₁. Крайние положения ползуна соответствуют угловым координатам кривошипа j = 0 и 180°.

Как уже отмечалось, при проектировании механизмов нужно учитывать весьма важный параметр, характеризующий условие передачи сил и работоспособность механизма, - угол давления 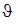(угол между вектором силы, приложенной к ведомому звену, и вектором скорости точки приложения движущей силы; трение и ускоренное движение масс при этом пока не учитываются). Угол давления не должен превышать допустимого значения: 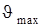£ 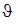_доп. Угол 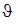при передаче усилия на ведомое звено отмечают на схеме механизма в зависимости от того, какое его звено является ведомым. Если им будет ползун 3, то сила `F<sub>32</sub> передается на него с углом давления 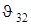, а если кривошип 1, то сила `F₁₂ составит угол 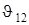с вектором скорости `n_В.

При ведомом кривошипе угол давления 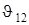два раза за цикл (когда шатун и кривошип располагаются на одной прямой) получает максимальное значение, равное 90°. Эти положения кривошип проходит только благодаря инерции вращающихся масс деталей, жестко связанных с кривошипом l.

Наибольший угол давления J_32max определяют путем исследования функции 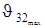= 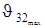(j) на максимум. Для центрального механизма (e = 0) максимальное значение угла давления J_32max= arcsin l₁/ l₂ будет при j = 90 или 270°. Следовательно, чем меньше значение l₂ = l₂/ l₁, тем меньше размеры механизма (по отношению к длине кривошипа), но больше углы давления. А с возрастанием величины J_32max, независимо от того, какое звено является ведомым, увеличивается усилие между ползуном и направляющей (между поршнем и стенкой цилиндра поршневой машины). Поэтому, например, для механизмов двигателей внутреннего сгорания l₂принято выбирать в пределах l₂ = 3...5, что соответствует значению J_32max= 19...11° (см.: Баранов Г.Г. Курс теории механизмов и машин. М., 1967).

Во внеосном кривошипно-шатунном механизме (рис. 4.4, в) ход ползуна (его максимальное перемещение) из DAC₁C₁¢и DAC₂C₂¢

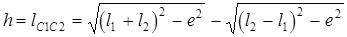(4.5)

откуда при заданных h, e и l₂ = l₂/ l₁ можно найти l₁ (например, методом интерполяционного приближения - задаваясь рядом значений l₁, близких к h/2, и проверяя равенство левой и правой частей уравнения). Максимальный угол давления J_32maxпри e < 0 , будет в положении, когда

j = 270°; если же e < 0, то при j = 90°.

Если заданы два положения кривошипа (рис. 4.5, б), определяемые координатами j₁и j₂, перемещение ползуна s_с (с учетом знака: на рис. 4.5, б S_с< 0) и отношения l₂ = l₂/ l₁ и l _е = e / l₁, то длины звеньев l₁ и l₂ определяют следующим образом.

Проецируя векторную цепь l₁ + l₂ на ось y , имеем для любого положения l₁sinj + l₂sin 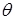= e, откуда угловая координата звена 2 в положениях 1 и 2:

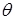_1,2 = arcsin[(l _е - sinj_1,2) / l₂].

Проецируя ту же цепь на ось x, имеем:

,

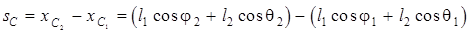откуда, после подстановки l₂ = l₂ l₁ получим

l₁ = s_C/[cosj₂ -cosj₁ + l₂(cos 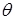₂ - cos 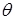₁)] (4.6)

Затем по величине l₂ находят l₂.

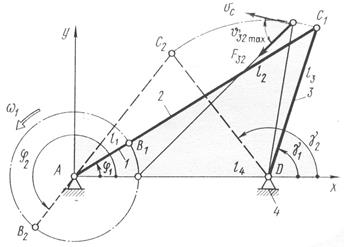
Кривошипно-коромысловый механизм (рис. 4.6). По заданным длине стойки l₄, длине ведомого коромысла l₃ и его координатам g₁, g₂ в крайних положениях неизвестные длины звеньев l₁ и l₂ находят следующим образом. Соединяя прямыми точки C₁ и C₂ с точкой A, имеем

; ,

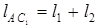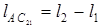откуда

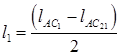; (4.7)

Максимальный угол давления 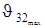будет при j=0 или 180°.

	Рис. 4.5

Рис. 4.6

Механизм с возвратно-вращающимся (качающимся) цилиндром. Этот механизм, применяемый в гидроприводах, изображен на рис. 4.7, а в крайних положениях AB₁C и AB₂C. При переходе из одного крайнего положения в другое поршень 2 перемещается на расстояние h (ход поршня), а ведомое коромысло 1 длиной l₁ поворачивается на нужный угол b. Чтобы полностью использовать цилиндр при перемещении поршня, задаются отношением длины цилиндра 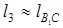к ходу поршня h в виде коэффициента k = l₃/h > 1, определяемого конструктивно; например, k = 1,3; 1,4 и т.д.

Рис. 4.7

Приходится также учитывать угол давления J как угол между осью цилиндра, по направлению которой передается усилие 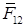, и вектором скорости 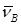точки приложения силы. Этот угол переменный, поэтому при проектировании задаются допускаемым углом давления J_доп, с тем, чтобы при работе механизма не превысить его.

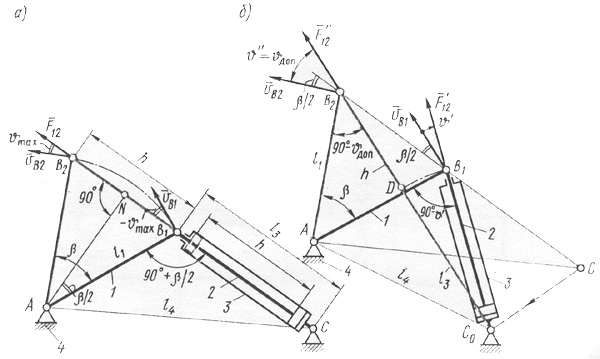
Синтез оптимальной по углам давления схемы такого механизма при заданных l₁, k, b ведут следующим образом (рис. 4.7, а). Построив два положения AB₁ и AB₂ ведомого звена 1, примем ход поршня 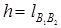. Отложив на продолжении прямой B₂B₁ отрезок 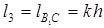, получим точку C. В крайних положениях механизма, как это видно из DAB₁N и DANB₂, угол давления по абсолютной величине будет наибольшим: J_max=b/2.

Во всех остальных положениях угол давления будет меньше, поскольку при переходе точки B из положения B₁ в положение B₂ он меняет свой знак и, следовательно, проходит через нулевое значение. Из DAB₁N

h=2l₁sin(b/2) (4.8)

Из DAB₁C, по теореме косинусов, длина стойки

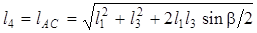(4.9)

При небольших углах b J_max может быть в данной схеме значительно меньше J_доп, и этот вариант кинематической схемы можно улучшить с точки зрения габаритов механизма путем уменьшения длины стойки l₄.

Оптимальную по габаритам схему механизма при условии J_max=J_доп получим следующим образом (рис. 4.7, б). Пусть заданы l₁, k, b, J_доп. Вычертив первый вариант схемы, переместим точку C в новое положение C₀ для которого угол давления в положении 2 механизма увеличится и будет равен допускаемому: J²=J_доп. При перемещении точки C угол давления в положении 1 также 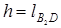< 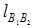; его можно найти, решая квадратное уравнение, полученное из DC₀B₁B₂ по теореме косинусов:

,

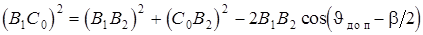где , , .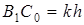

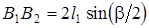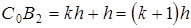Решение приводит к формуле

,

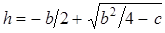где

;

.

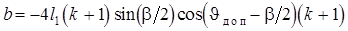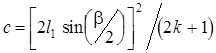После этого определяют 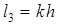и длину стойки из DAC₀B₂

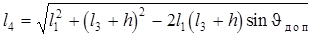(4.10)

Данный вариант кинематической схемы является весьма целесообразным для случая, когда нужно преодолевать большую нагрузку на ведомом звене в начале движения, поскольку угол давления 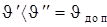, в результате чего увеличивается момент движущей силы 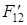относительно оси A и уменьшаются потери на трение в кинематических парах.

Кинематические пары следует подобрать так, чтобы механизм был статически определимым, или же , если это затруднительно, свести к минимуму число избыточных связей. В данном случае механизм будет статически определимым (без избыточных связей), если пара A вращательная, пары B и C сферические, пара поршень-цилиндр цилиндрическая. Тогда, учитывая, что число степеней свободы механизма W=W₀+ W_М=1+2=3 (две местные подвижности - независимые вращения поршня со штоком и цилиндра относительно своих осей), по формуле Малышева получим q=0.

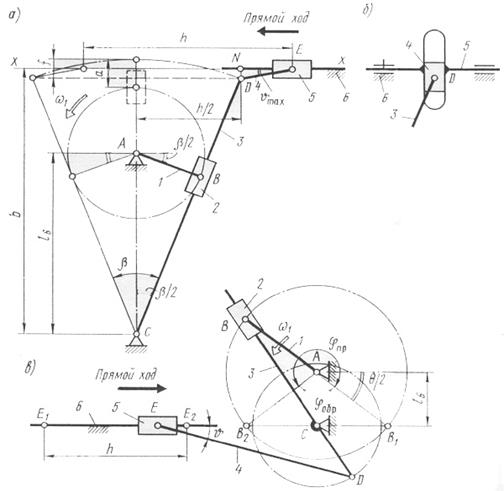
Механизм с качающейся кулисой. Шестизвенный кулисный механизм (рис. 4.8, а) преобразует вращательное движение кривошипа 1 в возвратно-поступательное движение ползуна 5, при этом средняя скорость v_обр ползуна при обратном ходе больше в K_v раз средней скорости v_пр прямого хода. Исходными данными обычно служит ход h выходного звена 5 и коэффициент изменения его средней скорости K_v= v_обр/ v_пр.

Например, в строгальных и долбежных станках изделие обрабатывается в одном направлении с заданной скоростью резания, а холостой (обратный) ход режущего инструмента осуществляется с большей средней скоростью; в этом случае K_v>1.

Коэффициент K_v и угол 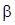размаха (угловой ход) кулисы связаны (при w₁=const) зависимостью

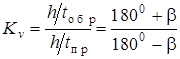(4.11)

откуда

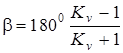(4.12)

Длину кулисы находят из рассмотрения ее крайнего положения по формуле

.

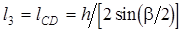В среднем (вертикальном) положении кулисы CD длины звеньев l₃, l₆=l_AC (стойки) и l₁=l_AB связаны соотношением

l₃= l₆+ l₁+a (4.13)

где размер a выбирают конструктивно с целью наиболее полного использования длины кулисы. С другой стороны, из прямоугольного DABC

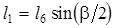(4.14)

Подстановка значений l₁ в выражение (4.13) дает длину стойки (межосевое расстояние)

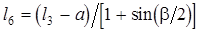(4.15)

После вычисления l₆ можно по формуле (4.14) найти l₁; для механизмов данного типа обычно .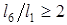

При ведущем кривошипе угол давления при передаче усилия от кулисного камня (ползуна) 2 к кулисе 3 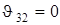, что является достоинством кулисных механизмов. Для обеспечения наименьших углов давления при передаче усилия от звена 4 к ведомому ползуну 5 целесообразно положение оси xx выбрать так, чтобы она делила стрелку сегмента f пополам. Тогда из прямоугольного DNDE длина звена 4

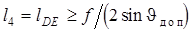(4.17)

где 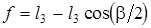; в этом случае будет обеспечено соотношение .

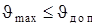Расстояние между осью вращения кулисы и осью направляющей ползуна 5 определяются по формуле

.

Рис. 4.8

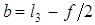Применяют и другой вариант двухповодковой группы звеньев 4, 5 с двумя поступательными и одной вращательной парами (рис. 4.8, б). По углам давления этот вариант лучше предыдущего: .

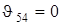Механизм с вращающейся кулисой. Схема наиболее часто встречающегося варианта такого механизма изображена на рис. 4.8, в. Исходные данные: длина 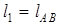кривошипа, ход h ползуна 5 и коэффициент изменения его средней скорости K_v= v_обр/ v_пр>1.

Прямой ход ползуна 5 совершает при повороте кривошипа 1 на угол 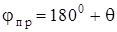, обратный - при повороте кривошипа на угол 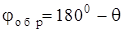. Поэтому при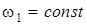

(4.18)

откуда

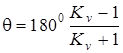(4.19)

Расстояние 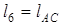между осями вращения кривошипа 1 и кулисы 3 из DAB₁C определяется по формуле

;

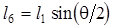Крайние положения точки E ползуна (E₁ и E₂) определяются положениями точки B (B₁ и B₂), когда направления кулисы 3 и шатуна 4 совпадают, поэтому длина кривошипа CD:

l_CD=h/2.

Длина шатуна 4 должна быть такой, чтобы максимальная величина угла давления 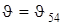не превосходила допускаемого значения 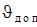, поэтому

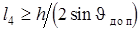(4.20)

Удлинять шатун 4 сверх полученного предела не следует, так как это увеличит габариты всего механизма. Для получения наименьших усилий в кулисной паре 2-3 (камень-кулиса) желательно выбрать длину кривошипа 1 как можно большей, однако следует учитывать, что при этом возрастают габариты механизма.

Методика решения более сложных задач синтеза рычажных механизмов по заданной непрерывной функции положения и по заданной траектории в данной лекции не рассматривается; см. об этом в [5].