Алгоритм скользящего окна

Методы коррекции ошибок в вычислительных сетях основаны на повторной передаче кадра данных в том случае, если кадр теряется и не доходит до адресата или приемник обнаружил в нем искажение информации. Чтобы убедиться в необходимости повторной передачи данных, отправитель нумерует отправляемые кадры и для каждого кадра ожидает от приемника так называемой положительной квитанции - служебного кадра, извещающего о том, что исходный кадр был получен и данные в нем оказались корректными. Время этого ожидания ограничено - при отправке каждого кадра передатчик запускает таймер, и, если по его истечении положительная квитанция на получена, кадр считается утерянным. Приемник в случае получения кадра с искаженными данными может отправить отрицательную квитанцию - явное указание на то, что данный кадр нужно передать повторно.

Существуют два подхода к организации процесса обмена квитанциями: с простоями и с организацией «окна».

Метод с простоями (Idle Source) требует, чтобы источник, пославший кадр, ожидал получения квитанции (положительной или отрицательной) от приемника и только после этого посылал следующий кадр (или повторял искаженный). Если же квитанция не приходит в течение тайм-аута, то кадр (или квитанция) считается утерянным и его передача повторяется. На рис. 4.2.11, а видно, что в этом случае производительность обмена данными существенно снижается, - хотя передатчик и мог бы послать следующий кадр сразу же после отправки предыдущего, он обязан ждать прихода квитанции. Снижение производительности этого метода коррекции особенно заметно на низкоскоростных каналах связи, то есть в территориальных сетях.

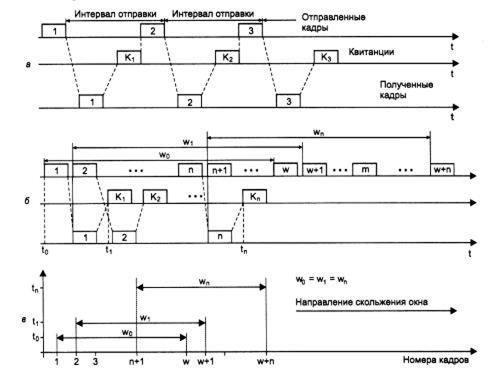
Рис. 4.2.11 Методы восстановления искаженных и потерянных кадров

Протокол TCP использует второй метод, который называется методом «скользящего окна» (sliding window). В этом методе для повышения коэффициента использования линии источнику разрешается передать некоторое количество кадров в непрерывном режиме, то есть в максимально возможном для источника темпе, без получения на эти кадры положительных ответных квитанций. Количество кадров, которые разрешается передавать таким образом, называется размером окна. Рисунок 4.2.11, б иллюстрирует данный метод для окна размером в W кадров.

В начальный момент, когда еще не послано ни одного кадра, окно определяет диапазон кадров с номерами от 1 до W включительно. Источник начинает передавать кадры и получать в ответ квитанции. Для простоты предположим, что квитанции поступают в той же последовательности, что и кадры, которым они соответствуют. В момент t1 при получении первой квитанции К1 окно сдвигается на одну позицию, определяя новый диапазон от 2 до (W+1).

Процессы отправки кадров и получения квитанций идут достаточно независимо друг от друга. Рассмотрим произвольный момент времени tn, когда источник получил квитанцию на кадр с номером n. Окно сдвинулось вправо и определило диапазон разрешенных к передаче кадров от (n+1) до (W+n). Все множество кадров, выходящих из источника, можно разделить на перечисленные ниже группы (рис. 4.2.11, б).

· Кадры с номерами от 1 до п. уже были отправлены и квитанции на них получены, то есть они находятся за пределами окна слева.

· Кадры, начиная с номера (п+1) и кончая номером (W+n), находятся в пределах окна и потому могут быть отправлены не дожидаясь прихода какой-либо квитанции. Этот диапазон может быть разделен еще на два поддиапазона:

o кадры с номерами от (n+1) до т, которые уже отправлены, но квитанции на них еще не получены;

o кадры с номерами от m до (W+n), которые пока не отправлены, хотя запрета на это нет.

· Все кадры с номерами, большими или равными (W+n+1), находятся за пределами окна справа и поэтому пока не могут быть отправлены.

Перемещение окна вдоль последовательности номеров кадров показано на рис. 4.2.11, в. Здесь t0 - исходный момент, t1 и tn - моменты прихода квитанций на первый и n-й кадр соответственно. Каждый раз, когда приходит квитанция, окно сдвигается влево, но его размер при этом не меняется и остается равным W. Заметим, что хотя в данном примере размер окна в процессе передачи остается постоянным, в реальных протоколах (например, TCP) можно встретить варианты данного алгоритма с изменяющимся размером окна.

Итак, при отправке кадра с номером n источнику разрешается передать еще W-1 кадров до получения квитанции на кадр n, так что в сеть последним уйдет кадр с номером (W+n-1). Если же за это время квитанция на кадр n так и не пришла, то процесс передачи приостанавливается, и по истечении некоторого тайм-аута кадр n (или квитанция на него) считается утерянным, и он передается снова.

Если же поток квитанций поступает более-менее регулярно, в пределах допуска в W кадров, то скорость обмена достигает максимально возможной величины для данного канала и принятого протокола.

Метод скользящего окна более сложен в реализации, чем метод с простоями, так как передатчик должен хранить в буфере все кадры, на которые пока не получены положительные квитанции. Кроме того, требуется отслеживать несколько параметров алгоритма: размер окна W, номер кадра, на который получена квитанция, номер кадра, который еще можно передать до получения новой квитанции.

Приемник может не посылать квитанции на каждый принятый корректный кадр. Если несколько кадров пришли почти одновременно, то приемник может послать квитанцию только на последний кадр. При этом подразумевается, что все предыдущие кадры также дошли благополучно.

Некоторые методы используют отрицательные квитанции. Отрицательные квитанции бывают двух типов - групповые и избирательные. Групповая квитанция содержит номер кадра, начиная с которого нужно повторить передачу всех кадров, отправленных передатчиком в сеть. Избирательная отрицательная квитанция требует повторной передачи только одного кадра.

Метод скользящего окна реализован не только в протоколе TCP, но и во многих других протоколах: LLC2, LAP-B, X.25, Novell NCP Burst Mode.

Метод с простоями является частным случаем метода скользящего окна, когда размер окна равен единице.