Физические величины

Основным объектом измерения в метрологии являются физические величины.

Физическая величина – одно из свойств физического объекта (физической системы, явления или процесса), общее в качественном отношении для многих физических объектов, но в количественном отношении индивидуальное для каждого из них. Можно сказать также, что физическая величина - это величина, которая может быть использована в уравнениях физики, причем, под физикой здесь понимается в целом наука и технологии.

В последнее время все большее распространение получает подразделение величин на физические и нефизические, хотя следует отметить, что пока нет строгого критерия для такого деления величин. При этом под физическими понимают величины, которые характеризуют свойства физического мира и применяются в физических науках и технике. Для них существуют единицы измерения. Физические величины в зависимости от правил их измерения подразделяются на три группы:

― величины, характеризующие свойства объектов (длина, масса);

― величины, характеризующие состояние системы (давление, температура);

― величины, характеризующие процессы (скорость, мощность).

К нефизическим относят величины, для которых нет единиц измерения. Они могут характеризовать как свойства материального мира, так и понятия, используемые в общественных науках, экономике, медицине.

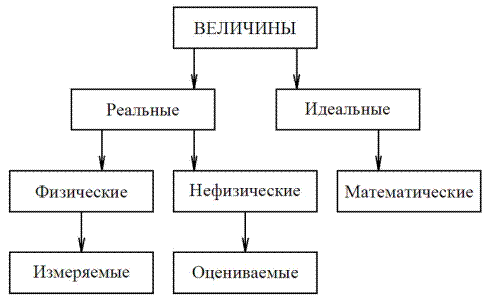
Таким образом, величины можно систематизировать следующим образом (рисунок 3).

Рисунок 3 – Классификация величин

Идеальные величины, главным образом, относятся к математике и являются обобщением (моделью) конкретных реальных понятий. Реальные величины делятся, в свою очередь, на физические и нефизические.

В соответствии с таким разделением величин принято выделять измерения физических величин и нефизические измерения. Другим выражением такого подхода являются два разных понимания понятия измерения:

― измерение в узком смысле как экспериментальное сравнение одной измеряемой величины с другой известной величиной того же качества, принятой в качестве единицы;

― измерение в широком смысле как нахождение соответствий между числами и объектами, их состояниями или процессами по известным правилам.

Второе определение появилось в связи с широким распространением в последнее время измерений нефизических величин, которые фигурируют в медико–биологических исследованиях, в частности, в психологии, в экономике, в социологии и других общественных науках. В этом случае правильнее было бы говорить не об измерении, а об оценивании величин, понимая оценивание как установление качества, степени, уровня чего–либо в соответствии с установленными правилами. Другими словами, это операция по приписыванию путем вычисления, нахождения или определения числа величине, характеризующей качество какого–либо объекта, по установленным правилам. Например, определение силы ветра или землетрясения, выставление оценки фигуристам или оценок знаний учащихся по пятибалльной шкале. Понятие оценивание величин не следует путать с понятием оценки величин, связанным с тем, что в результате измерений мы фактически получаем не истинное значение измеряемой величины, а лишь его оценку, в той или иной степени близкую к этому значению.

Таким образом, физические величины делятся на измеряемые и оцениваемые. Измеряемые физические величины могут быть выражены количественно в виде определенного числа установленных единиц измерения, возможность введения и использования последних является важным отличительным признаком измеряемых величин.

Совокупность чисел Q, отображающая различные по размеру однородные величины, должна быть совокупностью одинаково именованных чисел. Это именование является единицей физической величины или ее доли. Единица физической величины [Q] – это физическая величина фиксированного размера, которой условно присвоено числовое значение, равное единице и применяемое для количественного выражения однородных физических величин.

Значение физической величины Q – это оценка ее размера в виде некоторого числа принятых для нее единиц. Числовое значение физической величины q – отвлеченное число, выражающее отношение значения величины к соответствующей единице данной физической величины.

Уравнение Q=q[Q], где Q – физическая величина, для которой строится шкала; [Q] – ее единица измерения; q – числовое значение физической величины, называют основным уравнением измерения. Суть простейшего измерения состоит в сравнении физической величины Q с размерами выходной величины регулируемой многозначной меры q[Q]. В результате сравнения устанавливают, что q[Q] < Q < (q+l)[Q]. Измерение – познавательный процесс, заключающийся в сравнении путем физического эксперимента данной физической величины с известной физической величиной, принятой за единицу измерения.

Рассмотренное выше понятие «измерение», предполагающее наличие единицы измерения (меры), соответствует понятию измерения в узком смысле и является более традиционным и классическим. В этом смысле оно и будет пониматься ниже – как измерение физических величин.

Шкалы измерений

Физические величины, для которых по тем или иным причинам не может быть введена единица измерения, могут быть только оценены. Оценивают величины при помощи шкал.

Шкала величины – упорядоченная последовательность ее значений, принятая по соглашению на основании результатов точных измерений. Нефизические величины, для которых единица измерения в принципе не может быть введена, могут быть только оценены. Термины и определения теории шкал измерений изложены в документе МИ 2365–96.

В соответствии с логической структурой проявления свойств различают пять основных типов шкал измерений.

Шкалы наименований (шкалы классификации). Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности. Эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида не являются шкалами физических величин. Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен.

В шкалах наименований отнесение отражаемого свойства к тому или иному классу эквивалентности осуществляется с помощью органов чувств человека. Это наиболее адекватный результат, выбранный большинством экспертов. При этом большое значение имеет правильный выбор классов эквивалентной шкалы – они должны различаться наблюдателями, экспертами, оценивающими данное свойство. Нумерация объектов по шкале наименований осуществляется по принципу: "не приписывай одну и ту же цифру разным объектам". Числа, приписанные объектам, могут быть использованы только для определения вероятности или частоты появления данного объекта, но их нельзя применять для суммирования или других математических операций. Поскольку данные шкалы характеризуются только отношениями эквивалентности, то в них отсутствуют понятия нуля, "больше" или "меньше" и единицы измерения. Примером шкал наименований являются широко распространенные атласы цветов, предназначенные для идентификации цвета.

Шкалы порядка (шкалы рангов). Если свойство данного эмпирического объекта проявляет себя в отношении эквивалентности и порядка по возрастанию или убыванию количественного проявления свойства, то для него может быть построена шкала порядка.

Она является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство. В шкалах порядка существует или не существует нуль, но принципиально нельзя ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нет возможности судить, во сколько раз больше или меньше конкретные проявления свойства В случаях, когда уровень познания явления не позволяет точно установить отношения, существующие между величинами данной характеристики, либо применение шкалы удобно и достаточно для практики, используют условные (эмпирические) шкалы порядка. Условная шкала – это шкала физической величины, исходные значения которой выражены в условных единицах. Например, шкала вязкости Энглера, 12–балльная шкала Бофорта для измерения силы морского ветра.

Широкое распространение получили шкалы порядка с нанесенными на них реперными точками. К таким шкалам, например, относится шкала Мооса для определения твердости минералов, которая содержит 10 опорных (реперных) минералов с различными условными числами твердости: тальк – 1; гипс – 2; кальций – 3; флюорит – 4; апатит – 5; ортоклаз – 6; кварц – 7; топаз – 8; корунд – 9; алмаз – 10. Отнесение минерала к той или иной градации твердости осуществляется на основании эксперимента, который состоит в том, что испытуемый материал царапается опорным. Если после царапанья испытуемого минерала кварцем (G) на нем остается след, а после ортоклаза (F) – не остается, то твердость испытуемого материала составляет более 6, но менее 7. Более точного ответа в этом случае дать невозможно. В условных шкалах одинаковым интервалам между размерами данной величины не соответствуют одинаковые размерности чисел, отображающих размеры. С помощью этих чисел можно найти вероятности, моды, медианы, квантили, однако их нельзя использовать для суммирования, умножения и других математических операций.

Определение значения величин при помощи шкал порядка нельзя считать измерением, так как на этих шкалах не могут быть введены единицы измерения. Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным.

Шкалы интервалов (шкалы разностей). Эти шкалы являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. К таким шкалам относится летосчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо Рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов. На шкале интервалов определены действия сложения и вычитания интервалов. Действительно, по шкале времени интервалы можно суммировать или вычитать и сравнивать, во сколько раз один интервал больше другого, но складывать даты каких–либо событий бессмысленно.

Шкалы отношений. Эти шкалы описывают свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода – аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода – пропорциональные). Их примерами являются шкалы массы (второго рода) и термодинамической температуры (первого рода). В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений. С формальной точки зрения шкала отношений является шкалой интервалов с естественным началом отсчета. К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерении физических величин. Шкалы отношений – самые совершенные.

Абсолютные шкалы. Под абсолютными понимают шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначное определение единицы измерения и не зависящие от принятой системы единиц измерения. Такие шкалы соответствуют относительным величинам: коэффициенту усиления, ослабления и др.

Отметим, что шкалы наименований и порядка называют концептуальными, а шкалы интервалов и отношений метрическими (материальными). Абсолютные и метрические шкалы относятся к разряду линейных. Практическая реализация шкал измерений осуществляется путем стандартизации как шкал и единиц измерений, так и, в необходимых случаях, способов и условий их однозначного воспроизведения.