Главные радиусы кривизны в данной точке эллипсоида

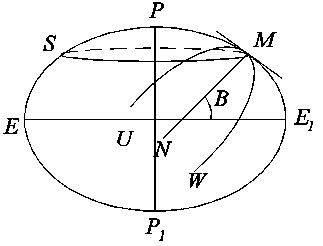
Рис. 2.2

Через нормаль к поверхности эллипсоида можно провести бесчисленное множество плоскостей.

Эти плоскости, перпендикулярные касательной плоскости к поверхности эллипсоида в данной точке, называются нормальными.

Кривые, образуемые от пересечения нормальных плоскостей с поверхностью эллипсоида, называются нормальными сечениями.

Из множества нормальных сечений в данной точке эллипсоида М можно выделить два главных сечения:

Меридианное сечение - сечение, проходящее через данную точку и оба полюса. На рис. 2.2 оно представлено эллипсом .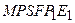

Сечение первого вертикала - сечение, проходящее через точку М и перпендикулярное меридианному эллипсу. На рис. 2.2 оно представлено кривой .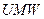

Радиус кривизны меридиана в данной точке М определяется выражением:

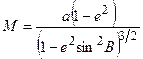. (2.4)

С возрастанием широты радиус М увеличивается. Так на экваторе (В = 0°) он равен

,

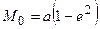а на полюсе (В = 90°)

.

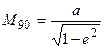Радиус кривизны первого вертикала в данной точке М, вычисляется по формуле:

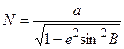. (2.5)

Из (2.5) следует, что на экваторе (В = 0°) он будет

,

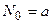а на полюсе (В = 90°)

.

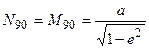Средний радиус кривизны в данной точке М равен среднему геометрическому величин М и N, т.е.

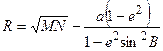, (2.6)

который на экваторе принимает значение:

,

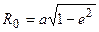а на полюсе равен

.

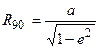И наконец радиус кривизны произвольного нормального сечения, заданного азимутом А, может быть определен из выражения:

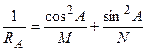. (2.7)