Измерительные приборы Сейсмограф

Для обнаружения и регистрации всех типов сейсмических волн используются специальные приборы — сейсмографы. В большинстве случаев сейсмограф имеет груз с пружинным прикреплением, который при землетрясении остаётся неподвижным, тогда как остальная часть прибора (корпус, опора) приходит в движение и смещается относительно груза. Одни сейсмографы чувствительны к горизонтальным движениям, другие — к вертикальным. Волны регистрируются вибрирующим пером на движущейся бумажной ленте. Существуют и электронные сейсмографы (без бумажной ленты).

Магниту́да землетрясе́ния (от лат. magnitudo — важность, значительность, крупность, величие) — величина, характеризующая энергию, выделившуюся при землетрясении в виде сейсмических волн. Первоначальная шкала магнитуды была предложена американским сейсмологом Чарльзом Рихтером в 1935 году, поэтому в обиходе значение магнитуды называют шкалой Рихтера.

Шкала Рихтера содержит условные единицы (от 1 до 9,5) — магнитуды, которые вычисляются по колебаниям, регистрируемым сейсмографом. Эту шкалу часто путают со шкалой интенсивности землетрясения в баллах (по 12-балльной системе), которая основана на внешних проявлениях подземного толчка (воздействие на людей, предметы, строения, природные объекты). Когда происходит землетрясение, то сначала становится известной именно его магнитуда, которая определяется по сейсмограммам, а не интенсивность, которая выясняется только спустя некоторое время, после получения информации о последствиях.

В теории расчета сооружений на сейсмические воздействия (теория сейсмичности), как и в других областях динамики различных механических систем, обычно применяются расчетные с распределенными и дискретными параметрами (массами). Система с дискретными параметрами хотя и носит приближенный характер, но более универсальна и можно получить решение для системы любой сложности, вследствие чего наиболее часто применяются в инженерных расчетах.

Для получения динамичных расчетных схем в виде системы с конечным числом степеней свободы, фактическая распределенная масса система концентрируется в определенных местах в виде материальных точек. В итоге получается невесомая система, несущая определенное количество сосредоточенных масс. Число степеней свободы система равно числу независимых геометрических параметров, однозначно определяющих положение сосредоточенных масс в произвольном моменте времени.

Массы рассматриваемой системы целесообразно сконцентрировать в местах, где сосредоточены значительные нагрузки. Достоверность и точность результатов расчета в значительной мере зависит от удачного выбора расчетной схемы, ее соответствия фактическим условиям работы сооружения.

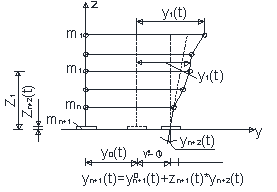
Рис. 55Расчетная схема здания, подвергающегося воздействию сейсмических нагрузок

В качестве примера рассмотрим методику расчета здания, имеющего и этажей на сейсмическом воздействии. Сконцентрировав массу звания на уровнях перекрытия и фундаментной плиты, получим систему в виде консольного стержня жестко заделанной в фундаментной плите, лежащей в условиях полного прилипания на поверхности упругого инерционного основания (рис. 55).

Будем рассматривать поперечные колебания стержня в плоскости (zy) Начало системы координат поместим в центре тяжести подошвы фундамента сооружения. Жесткость стержня по высоте изменяется по произвольному закону. На характер деформаций стержня не накладывается никаких ограничений, кроме требования линейной деформируемости.

Положение системы в произвольный момент времени t > 0 оп­ределяется линейными горизонтальными смещениями ( 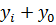),(i=1.2….n+1) (рис. 55).

Так как 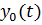есть перемещение грунтов основания при землетрясении на свободной поверхности земли, в предположении отсутствия сооружения, то оно здесь принимается заранее заданной величиной. Следовательно, если нам удастся определить величины 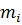(i=1,2,…,n+1), мы через значения этих величин в произвольный момент времени можем определить положение заданной системы.

Отсюда следует, что рассматриваемая система, располагая (n+1) количеством сосредоточенных масс, имеет (n + I) степеней свободы.

Колебания линейной системы при заданном внешней кинематическом воздействии 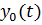полностью определяется ее инерционными и деформативными свойствами и параметрами рассеивания энергии. Инерционные свойства рассматриваемой системы характеризуются сосредоточенными массами 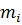(i=1,2,…,n+1), и характером их распределения по высоте. Деформативные свойства системы могут быть охарактеризованы при помощи единичных перемещений 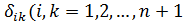), представляют собой горизонтальное перемещение точек i от действия единичной горизонтальной силы, приложенной в точке к. Перемещение в рамках принятой расчетной схемы определяется

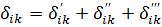
где 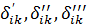горизонтальные перемещения точки i от действия единичной горизонтальной силы, приложенной в точке к, обусловленные соответственно: деформациями конструктивных элементов здания; относительным сдвигом между подошвой фундаментной плиты и основанием; поворотом подошвы фундаментной плиты относительно основания.

Выражение 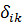можно записать в следующем виде

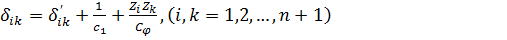(74)

Так как фундаментная плита считается абсолютно жесткой, поэтому при i=n+1, или k=n+1 следует принимат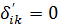ь Здесь 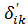определяется по формуле Мора; 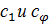— являются коэффициентами квазистатической жесткости основания при равномерном сдвиге и неравномерном сжатии или растяжении и их значения можно определить по следующим соотношениям.

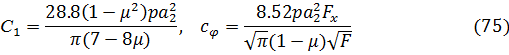
Где приняты следующие обозначения: 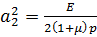- скорость распространения поперечных волн в грунтах; р — плотность грунтов основания; F—площадь подошвы фундаментной плиты; 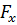— момент инерции площади подошвы фундаментной плиты относительно оси х.

Для учета рассеивания энергии при колебаниях системы воспользуемся теорией Фойгта, согласно которой диссипативные Силы прикладываются к сосредоточенным массам в состоянии движения системы, величина которых пропорциональна скорости движения сосредоточенных масс. Коэффициенты пропорциональности для рассматриваемой системы определяются по формуле

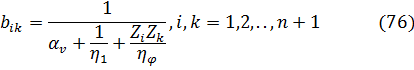
Величина 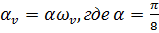— логарифмический декремент колебания, характеризует рассеивания энергии по корректированной гипотезе Фойгта за счет внутреннего неупругого сопротивления материалов конструкций при их деформации; 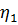— характеризует излучение энергии в основании за счет сдвиговых деформаций, происходящих на контактной поверхности между фундаментной плитой и основанием; 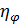— коэффициент рассеивания энергии за счет неравномерных линейных деформаций, происходящих на контактной поверхности между фундаментной плитой и основанием.

Акустическое сопротивление основания при равномерном сдвиге 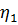и неравномерного сжатия и растяжения 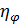определяются по известным соотношениям.

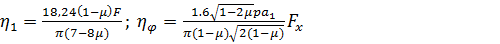(77)

Где 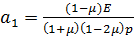— скорость распространения продольных волн в грунтовом основании.

Воспользуемся методом сил и запишем величину перемещения yi(t) произвольной массы с номером i=1,2,…n+1 , от действия сил инерции и сил учитывающих рассеивание энергии в рассматриваемой системе:

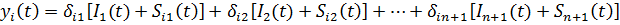(78)

Здесь 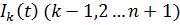сила инерции, действующая на k-ю массу и определяется по принципу Даламбера:

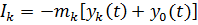(79)

Сила сопротивления 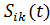, возникающая в к-й массе, согласно гипотезе Фойгта, прямо пропорциональна величине скорости его движения:

Подставляя выражения (79) и (80) в (78) и после некоторых преобразований получим дифференциальное уравнение движения заданной системы в следующем виде:

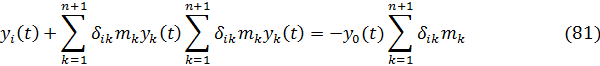
Для расчета сооружений на сейсмические воздействия справедливы нулевые начальные условия, та. предполагается, что до начала землетрясения сооружение находится в состоянии покоя. При землетрясении сооружение, переходя в движение, ее состояние характеризуется системой уравнений (81).

Для расчета системы дифференциальных уравнений (81) применяется метод преобразования Лапласа, т.е. искомые функции находятся по формуле

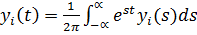(82)

где 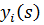является изображением функции y_i(t) по Лапласу и опре­деляется по формуле

Подставляя (82) в (81) и с учетом нулевых начальных условий задачи, получим:

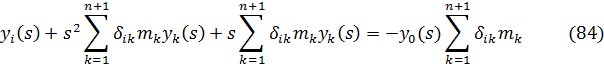
Последнее представляет систему алгебраических уравнений от­носительно перемещений в изображениях Лапласа.

Решение (84) в изображениях записывается в виде

Где 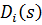— представляет собой определитель системы неоднородных алгебраических уравнений (84);D(s) — определитель той же системы при неизвестных .

Применяя к выражению (85) операции обратного преобразования Лапласа с применением теоремы сверло, получим решение задачи в следующем виде:

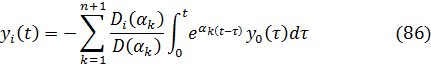
В традиционных методах расчета сооружения на сейсмостойкость, как правило, применяется следующее упрощающее допущение, что основание сооружения является абсолютно твердым телом, т.е. с = ¥ и с₁ = ¥. Если исходить из условия существования полного прилипания между фундаментной плитой и основанием на их контактной поверхности, очевидно, что масса с номером n+1, фундаментная плита полностью повторяет закон движения основания. С другой стороны, так как закон движения основания в данном случае считается исходной известной функцией, следовательно, закон движения фундаментной плиты тоже следует считать известной величиной. Поэтому число степеней свободы рассматриваемой системы (см. рис. 55) на одну единицу уменьшается и принимает значение равное n

Искомыми величинами в данном случае являются перемещения сосредоточенных масс с номерами i=1,2..n.

С учетом данного обстоятельства уравнение движения сооружения из (74) упрощается и принимает вид

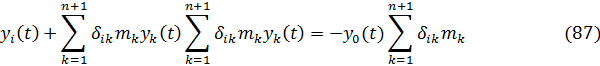
Для решения системы дифференциальных уравнений (87) с постоянными коэффициентами применяется метод разложения колебаний по формам, основанный на методе разделения переменных, те.

(88)

Сначала, для определения собственной частоты и собственного вектора 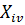, рассматриваются собственные колебания системы без учета сил сопротивления. В данном случае из (87) получим уравнения движения системы без учета сил сопротивления в свободном режиме колебаний

Подставляя решение (88) в (90), с учетом условий ортогональности собственных форм колебаний, т.е.

и после ряда преобразований получим

Выполнение этих равенств для произвольного значения t возможно лишь в том случае, если каждая из них в отдельности равна одной и той же постоянной при любом значении v. Обозначив эту постоянную через 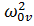, получим

Последние уравнения представляют собой систему n линейных однородных алгебраических уравнений относительно неизвестных 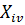для каждой v= 1,2... n формы колебаний.

Для определения ненулевых решений системы (92) необходимо обеспечить равенство нулю ее детерминанта

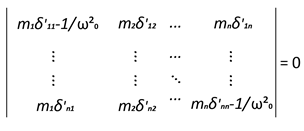
В развернутом виде это выражение представляет собой алгебраическое уравнение n-й степени относительно 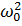. Корни этого уравнения вещественны, положительны и в большинстве случаев отличны друг от друга. Таким образом, из решения (93) определяется я положительных значений 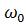, которые а возрастающем порядке 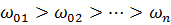являются собственными частотами системы без учета ее диссипативных свойств.

После определения собственных частот из решения системы (92) определяются значения собственных векторов для каждой v-й формы колебаний.

Для определения решения уравнений движения системы в вынужденном режиме колебаний подставим выражение (88) в уравнения (87) и с учетом условий ортогональности (90), получим

)

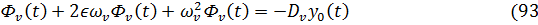где приняты следующие обозначения:

При нулевых начальных условиях, решая дифференциальное уравнение (94) подставляя в (88), окончательно получим

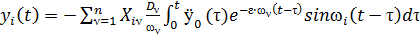(95)

Где 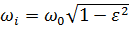— называется частотой собственных колебаний

с учетом диссипативных свойств системы.

Как показывает уравнение (94), применение принципа разложения колебаний по собственным формам позволяет рассматривать колебания линейно деформируемых систем по отдельным формам независимо от колебаний по другим формам, вследствие чего системы со многими степенями свободы рассчитываются, как системы с одной степенью свободы для каждой отдельной формы.

Указанный подход позволяет при рассмотрении системы со многими степенями свободы оценить динамический эффект внешнего воздействия через значения коэффициента динамичности для системы с одной степенью свободы.

Сейсмические колебания системы с одной степенью свободы из (79) принимают вид:

откуда

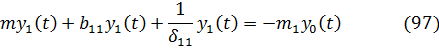
Последнее уравнение можно записать в виде

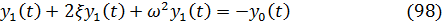
Где ,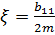

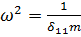
Решение последнего уравнения имеет вид

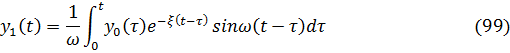
Дважды дифференцируя последнее выражение, получим относительное ускорение y{t), после суммирования y{t) с 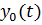получим последнее ускорение системы с одной степенью свободы в следующем виде:

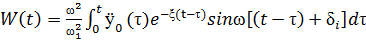, (100)

Где 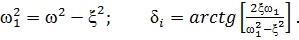(101)

Коэффициент динамичности в данном случае определяется по формуле

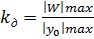(102)

Примерный вид графика ускорения колебания грунтов при сей­смических воздействиях представлен на рис. 56

Из обобщенного анализа более тридцати различных землетрясений ускорений колебаний грунтов 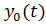был установлен график коэффициента динамичности (обеспеченность Р= 0.98) и имеет вид, представленный на рис. 56

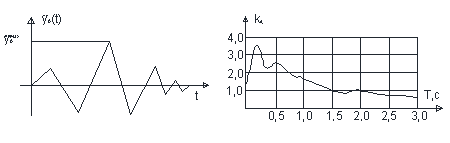
Рис. 56 График коэффициента динамичности