Использование симметрии при расчёте рам на устойчивость. Критерии выбора опасной формы потери устойчивости.
Если рама симметрична и симметрично нагружена, то форма потери устойчивости может быть либо прямосимметричная, либо обратносимметричная.
Пусть дана симметричная и симметрично нагруженная рама (рис.87) .
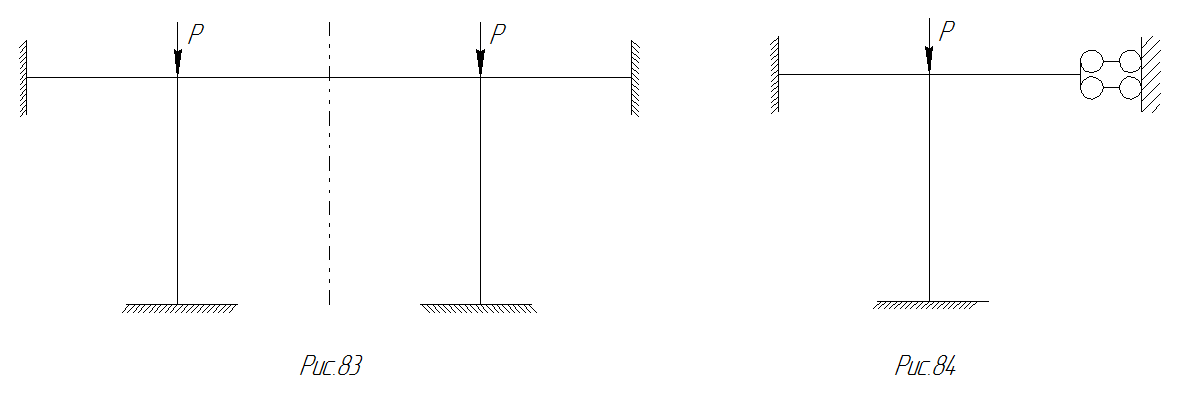
Рис. 87 Симметрично нагруженная Рис. 88 Расчетная схема
Рама для прямосимметричной
формы деформации
Расчётная схема для прямосимметричной формы деформации рамы (рис.88) и расчётная схема для обратносимметричной формы деформации (рис.89) имеют число степеней свободы в два раза меньше, чем заданная рама.
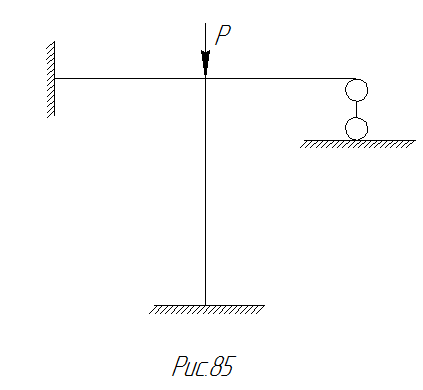
Рис. 89 Расчётная схема для обратносимметричной формы деформации
Рассчитав обе расчетные схемы, найдём 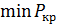 , соответствующую опасной форме потери устойчивости.
, соответствующую опасной форме потери устойчивости.
Однако, какая из двух форм потери устойчивости является опасной, прямосимметричная или обратносимметричная можно предвидеть заранее по определённым критериям.
Имеются три критерия определения опасной формы потери устойчивости симметричных и симметрично нагруженных рам:
1. Если ось симметрии совпадает с осью стойки рамы, то опасная форма потери устойчивости будет обратносимметричная как для свободной, так и для несвободной рам.
2. Если в несвободной раме ось симметрии пересекает ригель, то опасная форма потери устойчивости будет прямосимметричная.
3. Если в свободной раме ось симметрии пересекает ригель, то опасная форма потери устойчивости будет обратносимметричная.
Доказательство критериев основано на следующей лемме: величина критической нагрузки прямопропорциональна жёсткости системы.
Очевидно, что первые два критерия доказываются аналогично соответствующим критериям для свободных колебаний.
Докажем 3-й критерий определения опасной формы потери устойчивости.
Пусть дана симметричная и симметрично нагруженная свободная рама (рис.90,а.). Возможны как прямосимметричная, так и обратносимметричная формы потери устойчивости (рис. 90, б, в).
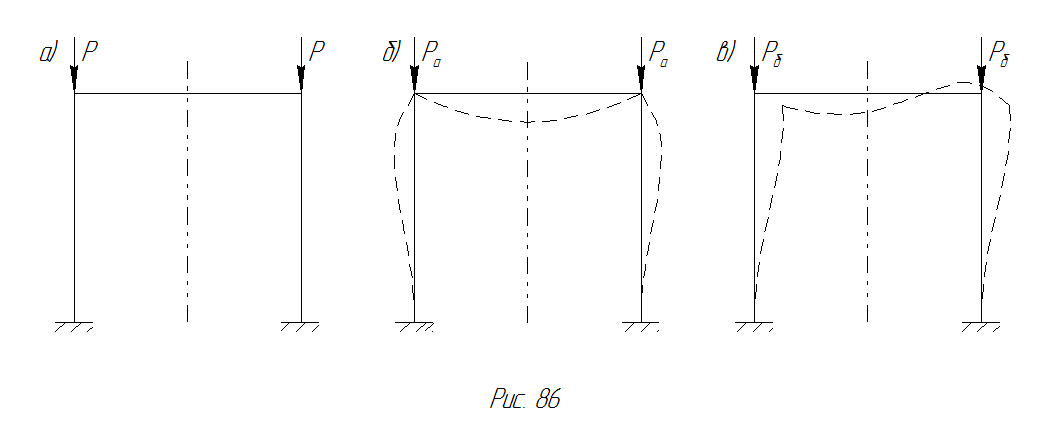
Рис. 90 Расчетчная схема прямосимметричной, так и обратносимметричной формы потери устойчивости рамы
Заметим, что при прямосимметричной форме деформации узлы рамы не смещаются по горизонтали, т.е. расчётная схема может быть принята как рама несвободная. Если при этом узлы рамы сделать шарнирными, т.е. ослабить жёсткость рамы (рис. 91), то согласно выше указанной лемме 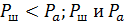 так же как и нижеприведённые Рж и Рб являются критическими силами, каждая из которых соответствует одной из расчетных схем, показанных на рис. 91-92
так же как и нижеприведённые Рж и Рб являются критическими силами, каждая из которых соответствует одной из расчетных схем, показанных на рис. 91-92
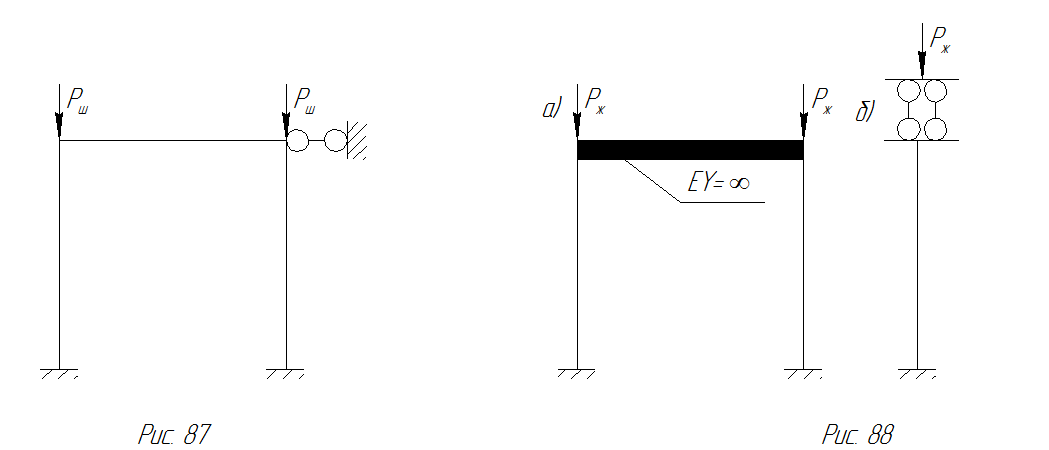
Рис. 91 Расчетная схема рамы Рис. 92 Расчетная схема рамы
с ослабленной жесткостью с увеличенной жесткостью
Теперь увеличим жёсткость ригеля свободной рамы до бесконечности (рис. 92, а). Очевидно, что для этой схемы
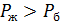
Так как расчётные схемы, показанные на рис. 92, а и б эквиваленты, то
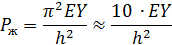
Учитывая, что
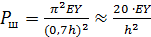
Имеем 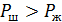 .
.
Следовательно, получим 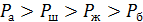 , то есть
, то есть 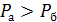
Таким образом, Рб есть минимальная критическая сила, т.е. обратносимметричная форма потери устойчивости является опасной.
Критерии определения устойчивости упругих систем
В теории устойчивости основными критериями определения критических значений внешних нагрузок являются энергетический, динамический и статический.
Энергетический критерий
В основе энергетического критерия заложен известный принцип Лагранжа-Дирихле, согласно которому, если система находится в состоянии устойчивого равновесия, ее полная потенциальная энергия обладает минимумом по сравнению со всеми соседними состояниями системы; если в состоянии неустойчивого равновесия - то максимумом; а если в безразличном, т.е. критическом - то потенциальная энергия является постоянной величиной.
В общем случае изменение (вариацию) полной потенциальной энергии системы dU при переходе ее от рассматриваемого состояния к соседнему можно записать таким образом:
dU = dV - dT,
где dV - вариация потенциальной энергии внутренних сил; dT -вариация потенциальной энергии внешних сил.
Следовательно, критическое состояние системы, согласно энергетического критерия, определяется из условия
dU = 0 или dV = dT.
Динамический критерий
При решении задач устойчивости по динамическому критерию исходят из предположения, что колеблющаяся система около своего положения равновесия, не способна возвращаться к первоначальному положению. Данное предположение равносильно утверждению, что в критическом состоянии спектр собственных частот рассматриваемой системы стремится к нулю, т.е. 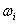 = 0 (i = 1, 2, 3, ...). Здесь
= 0 (i = 1, 2, 3, ...). Здесь 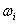 - собственная частота рассматриваемой системы при i-ой форме колебаний.
- собственная частота рассматриваемой системы при i-ой форме колебаний.
Следовательно, при решении задач по динамическому критерию составляется уравнение собственных колебаний заданной системы, далее определяется выражение частот собственных колебаний и из условия их равенства нулю определяется критическое значение внешних сил.
Так например, для сжатого осевой продольной силой P стержня постоянного поперечного сечения с распределенной массой, частота основного тона поперечных колебаний выражается формулой
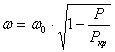 ,
,
где 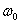 - собственная частота поперечных колебаний при отсутствии сжимающей силы, т.е. при P = 0.
- собственная частота поперечных колебаний при отсутствии сжимающей силы, т.е. при P = 0.
Очевидно, что при P->Pкр, ω->0,и период колебаний T=2π/ω->∞,т.е. стержень, колеблющийся около своего положения равновесия, не способен возвращаться к первоначальному состоянию.
Статический критерий
Суть статического критерия заключается в следующем. Исследуемой системе задается отклоненная форма равновесия, совпадающая по характеру перемещений с ожидаемой новой формой равновесного состояния системы после потери устойчивости системы, и определяются значения рассматриваемых внешних нагрузок, способных удержать систему в новой форме равновесного состояния.
Значения внешних нагрузок, способных удержать систему в новом равновесном состоянии, при соблюдении граничных условий по исходному состоянию, является критическим.
В дальнейшем, здесь рассматривается решение задач теории устойчивости с применением только статического критерия, так как он является основным критерием при выполнении практических расчетов упругих консервативных систем.
Энергетический метод определения
критических нагрузок
Изучая формы равновесия шарика, расположенного на дне или вершине сферы, можно заметить, что всякому возможному отклонению шарика от его устойчивого равновесия (рис. 57,а) соответствует возрастание потенциальной энергии положения и, наоборот, убывание потенциальной энергии - отклонению от неустойчивого равновесия (рис. 57,б).
Аналогичные признаки устойчивого и неустойчивого равновесия имеют место и в упругом теле.
Критическому состоянию будет соответствовать случай, когда потенциальная энергия при малых возможных отклонениях от заданной формы равновесия остается постоянной.
Если мы будем рассматривать не саму потенциальную энергию, а ее изменение при переходе из одного положения равновесия в другое, то критическое состояние будет определяться условием
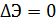 .
.
Изменение потенциальной энергии при переходе одного вида равновесия в другой будет складываться из двух величин:
1) изменения энергии положения нагрузки, равного работе действующих сил –w:
2) изменения потенциальной энергии внутренних сил - u.
Следовательно, условием критического состояния будет служить уравнение
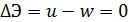 .
.
Получили уравнение устойчивости упругой системы, из которого и находятся критические силы.
Система рассматривается в отклоненном состоянии, бесконечно близком к первоначальному, и составляется в общем виде работа внешних сил, которая приравнивается дополнительно накапливаемой потенциальной энергии деформации:
w=u (145)
Это равенство составляется с точностью до бесконечно малых второго порядка. Его применение покажем на примере упруго закрепленного стержня с бесконечной жесткостью (рис.93).
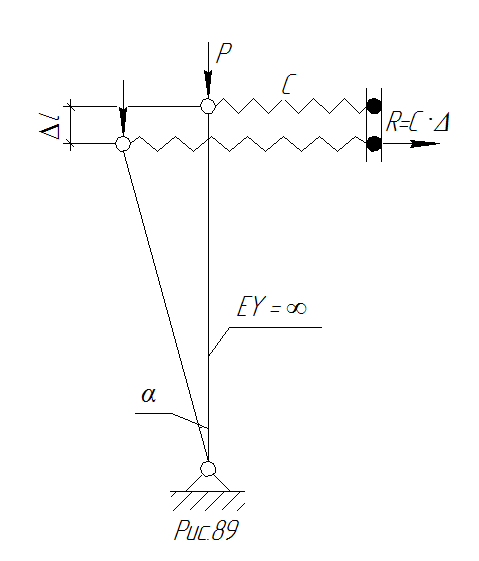
Рис. 93 Расчетная схема упруго закрепленного стержня с бесконечной жесткостью
В критическом состоянии стержень, очевидно, отклонится на угол 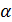 . При этом сила Ркр сместится влево на расстояние
. При этом сила Ркр сместится влево на расстояние  за счет растяжения пружины с жесткостью С и опустится вниз на
за счет растяжения пружины с жесткостью С и опустится вниз на  за счет поворота стержня. В пружине возникает реакция
за счет поворота стержня. В пружине возникает реакция 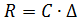
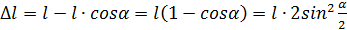 (146)
(146)
По малости угла α принимаем
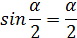
Равенство (146) примет вид:
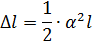
Тогда работа внешних сил будет равна:
 (147)
(147)
Приращение упругой потенциальной энергии за счёт деформации пружины
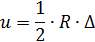
Учитывая, что 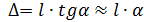 ,
,
Имеем 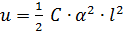 (148)
(148)
Подставляя выражения(147) и (148) в равенство (145), получим:
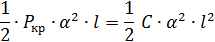
Откуда 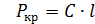 (149)
(149)
Исследуем энергетическим способом продольный изгиб стержня переменной жёсткости 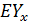 (рис.94).
(рис.94).
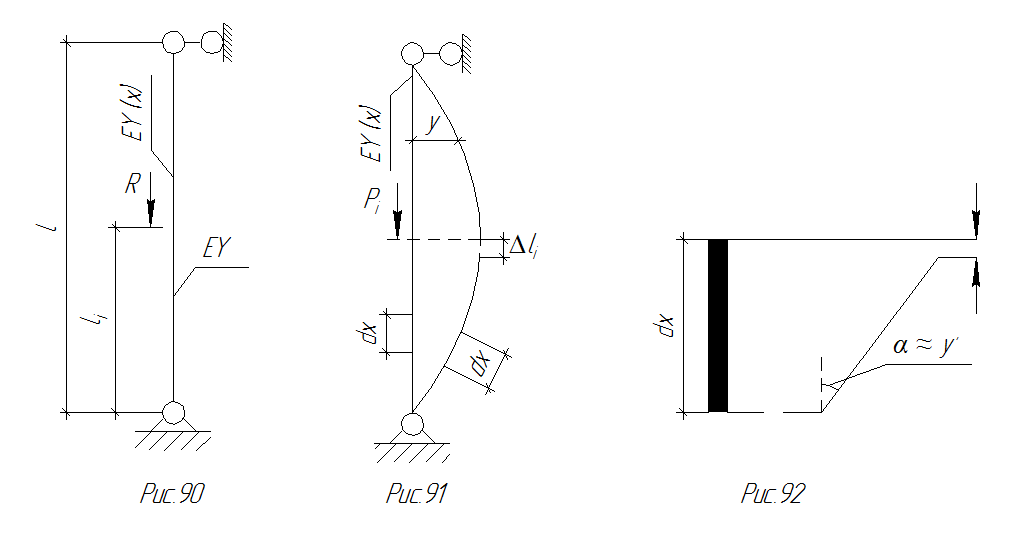
Рис.94 Схема продольного Рис.95Схема деформи- Рис.96 Выделенный
изгиба стержня рованного стержня про- элемент стержня
переменной жесткости дольной силой длиной dx
Все нагрузки заданы соотношением
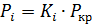 ,
,
Где 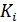 – коэффициент пропорциональности.
– коэффициент пропорциональности.
После потери устойчивости стержень изогнётся (рис.95) и сила Pi опустится на величину ∆li.
Выделим в стержне элемент длиной dx (рис.96). Так как
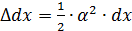 и
и 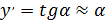 , то
, то 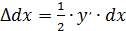 . Тогда
. Тогда
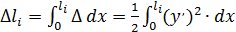 (150)
(150)
Работа внешних сил равна
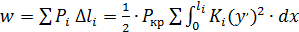 (151)
(151)
Работа внутренних сил или потенциальная энергия деформации равна:
 (152)
(152)
или, учитывая, что 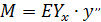 ,
,
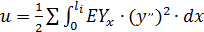 (153)
(153)
Из равенства w=uследует:
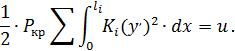
Тогда 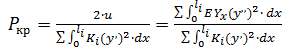 (154)
(154)
Пример. Шарнирно-закреплённый стержень длиной l и с жёсткостью EY сжат силой Р (рис.97)
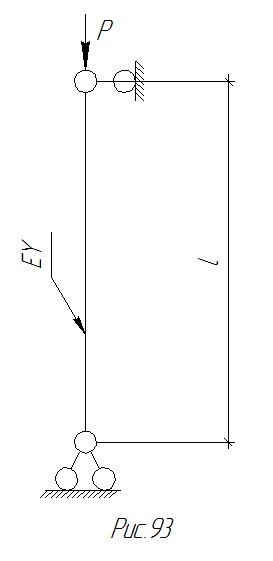
Рис. 97 Расчетная схема шарнирно-закреплённого стержня длиной L и с жёсткостью EY
Требуется определить критическое значение силы Р
Зададим упругую линию в виде синусоиды 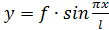 .
.
Соответственно 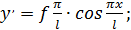
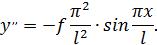
Тогда 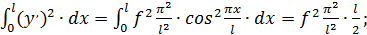
и 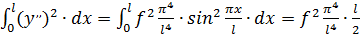
Подставляя полученные результаты в формулу (154), получим:
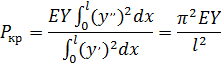
Полученный результат совпадает с точным решением, так как упругой линией задались точно.
При расчете на устойчивость стержня переменного сечения уравнением упругой оси приходится задаваться приближенно. Так, например, проф. Тимошенко рекомендует аппроксимировать упругую ось следующим многочленом:
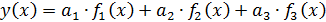 ,
,
где коэффициенты Q1,Q2,Q3 – неизвестные параметры, а функции f1(x),f2(x),f3(x) нам известны.
Функции fi(x) принимаются таким образом, чтобы выполнялись граничные условия. Например, при продольном изгибе шарнирно закреплённого стержня можно принять:
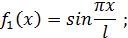
 (155)
(155)
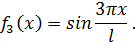
Энергетический метод в указанной приближённой форме всегда дает завышенное значение для критической нагрузки, так как систему с бесконечно большим числом степеней свободы мы сводим к системе с конечным числом степеней свободы и тем самым как бы накладываем на нее дополнительные связи.
Завышенное значение критической нагрузки позволяет воспользоваться условием минимума для выражения (154).
Из условия минимума критической нагрузки следует, что
 (156)
(156)
Подставив в (156) выражение (154) и взяв частные производные по всем независимым параметрам 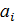 , получим систему линейных однородных уравнений относительно параметров
, получим систему линейных однородных уравнений относительно параметров 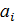 . Приравняв нулю главный определитель системы, составленный из коэффициентов при
. Приравняв нулю главный определитель системы, составленный из коэффициентов при 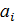 , получим условие для определения
, получим условие для определения 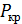 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Расчет ветровых нагрузок на здание и сооружение. Основы проведения аэродинамических испытаний | | | С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ |
Дата добавления: 2017-01-26; просмотров: 3626;











